Четырехугольные призмы являются одними из наиболее распространенных геометрических тел, используемых в различных областях науки и техники. Они состоят из двух параллельных четырехугольников, называемых основаниями, и боковых граней, которые соединяют соответствующие вершины оснований.
Одним из самых важных параметров четырехугольной призмы является ее высота. Высоту призмы можно определить различными способами, в зависимости от известных данных. Один из таких способов - использование диагонали призмы.
Диагональ призмы - это прямая линия, соединяющая две противоположные вершины оснований. Она проходит через центр призмы и делит ее на два равных треугольника. Используя данную информацию, можно найти высоту призмы через длину ее диагонали.
Как определить высоту четырехугольной призмы через диагональ?
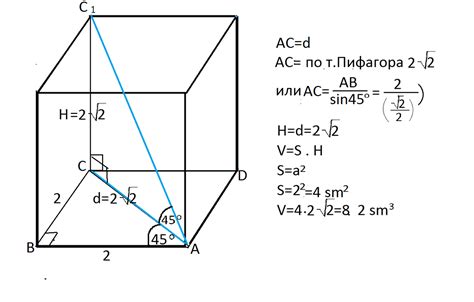
Чтобы определить высоту четырехугольной призмы через диагональ, необходимо вычислить длину этой диагонали и затем применить соответствующую формулу.
1. Найдите длины сторон основания четырехугольной призмы. Это можно сделать с помощью известных длин сторон или координат четырех вершин основания.
2. Рассчитайте длину диагонали основания призмы. Для четырехугольной призмы это можно сделать, используя формулу расстояния между двумя точками в координатной плоскости или теорему Пифагора.
3. Используя формулу для объема четырехугольной призмы (V = S * h, где V - объем, S - площадь основания, h - высота), выражайте высоту h в зависимости от длины диагонали и длины сторон основания.
4. Подставьте значения длины диагонали и длин сторон основания в полученную формулу и решите уравнение для определения высоты четырехугольной призмы.
5. Полученное значение будет высотой четырехугольной призмы через диагональ основания.
Примечание: важно учесть, что в разных случаях могут использоваться разные формулы и методы для нахождения высоты четырехугольной призмы. При работе с четырехугольными призмами также нужно учитывать их форму и свойства.
Что такое четырехугольная призма?
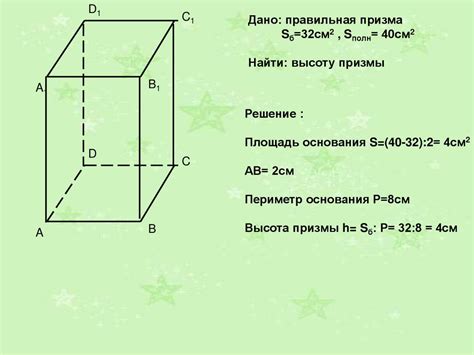
Четырехугольная призма имеет два прямых и четыре наклонных ребра. Все эти ребра являются отрезками прямых линий. Для четырехугольной призмы также характерны три оси симметрии: две оси проходят через противоположные вершины, а третья ось проходит через середины противоположных ребер.
Объем четырехугольной призмы может быть вычислен как произведение площади основания на высоту призмы. Высота призмы - это расстояние между основаниями, измеряемое вдоль оси симметрии. Для вычисления высоты призмы часто используют геометрические свойства и формулы.
Четырехугольные призмы являются одними из наиболее распространенных призм, которые применяются в геометрии и различных областях науки и техники. Они имеют множество применений, включая структурное моделирование, черчение, архитектуру, инженерное проектирование и многое другое.
| Пример четырехугольной призмы: |
|---|
 |
Как найти длину диагонали четырехугольной призмы?
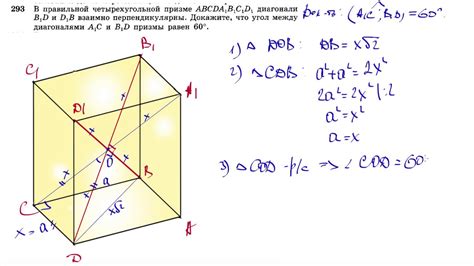
Для того чтобы найти длину диагонали четырехугольной призмы, необходимо знать его геометрические параметры, такие как длина ребра основания и высота призмы.
Для начала, определите длину ребра основания призмы. Если даны размеры сторон основания, можно использовать теорему Пифагора для нахождения длины диагоналей основания. Эта теорема гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Таким образом, для прямоугольного основания с катетами a и b, длина диагонали D вычисляется по формуле:
D = √(a² + b²)
Зная длину ребра основания и длину диагонали, можно найти высоту призмы. Для этого используется теорема Пифагора для правильного треугольника, образованного ребром высоты, половиной диагонали основания и длиной диагонали. Получается:
h² = D² - (a/2)²
где h - высота призмы.
Округляйте полученные значения длины диагоналей и высоты призмы до необходимой точности и используйте их для дальнейших рассчетов.
Таким образом, вы можете найти длину диагонали четырехугольной призмы, зная длину ребра основания и высоту призмы.
Формула для определения высоты четырехугольной призмы через диагональ
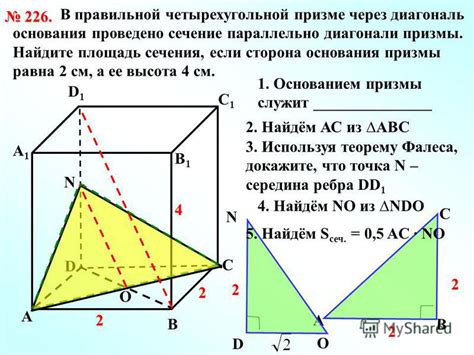
Для четырехугольной призмы с основанием в форме четырехугольника, можно использовать следующую формулу:
- Высота = (2 * Площадь) / (Длина диагонали)
Чтобы получить высоту, необходимо умножить площадь основания на 2 и разделить на длину диагонали.
Определение высоты призмы имеет важное значение при выполнении различных геометрических и физических расчетов. Учитывая, что призмы могут иметь различную форму основания, формула для расчета высоты может варьироваться в зависимости от типа призмы.
Пример расчета высоты четырехугольной призмы через диагональ
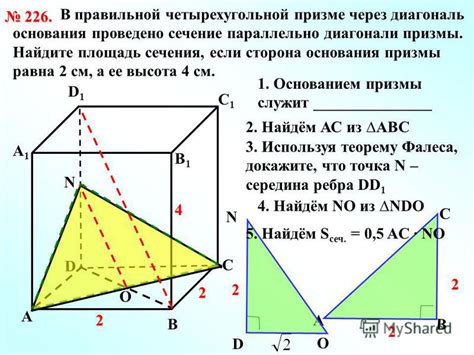
Для нахождения высоты четырехугольной призмы через диагональ необходимо знать длину диагонали и размеры основания призмы.
Предположим, у нас есть четырехугольная призма с основанием в форме четырехугольника ABCD и диагональю DB.
Для расчета высоты призмы воспользуемся теоремой Пифагора.
- Рассмотрим основание ABCD и соединим его диагоналями AC и BD.
- Обозначим длину диагонали DB как d и расстояние от вершины A до середины диагонали DB как h.
- Используя теорему Пифагора для треугольника ABD, получим следующее равенство: AB^2 + BD^2 = AD^2.
- Подставим значения сторон AB и BD через известные величины d и h: (AB/2)^2 + d^2 = AD^2.
- Длина стороны AB равна половине диагонали AC, то есть AB = AC/2.
- Расстояние AD равно h + высоте призмы.
- Подставим полученные значения в выражение: (AC/2)^2 + d^2 = (h + высота)^2.
- Разрешим уравнение относительно высоты призмы и найдем ее значение.
Таким образом, зная длину диагонали и размеры основания призмы, мы можем рассчитать ее высоту, используя теорему Пифагора. Не забудьте подставить правильные значения и правильно расчеты, чтобы получить точный результат.