Цилиндр - это геометрическое тело, форма которого напоминает банку из-под консервов или свечу. Один из основных параметров цилиндра - его высота. Однако, иногда задача состоит в том, чтобы найти высоту цилиндра, если известны другие параметры, такие как площадь боковой поверхности и диаметр основания. В данной статье мы рассмотрим, как решить эту задачу.
Для начала, вспомним, что боковая поверхность цилиндра представляет собой прямоугольник, высота которого равна высоте цилиндра, а ширина равна длине окружности его основания. Площадь боковой поверхности цилиндра можно найти по формуле:
S = 2πrh
где S - площадь боковой поверхности цилиндра, π - число пи (примерно равно 3.14), r - радиус основания цилиндра, h - высота цилиндра.
Теперь, когда у нас есть формула для нахождения площади боковой поверхности цилиндра, и мы знаем диаметр основания цилиндра, можем найти радиус основания, разделив диаметр на 2. Затем, для нахождения высоты цилиндра, подставим известные значения в формулу и решим уравнение относительно h.
Определение высоты цилиндра по площади боковой поверхности и диаметру
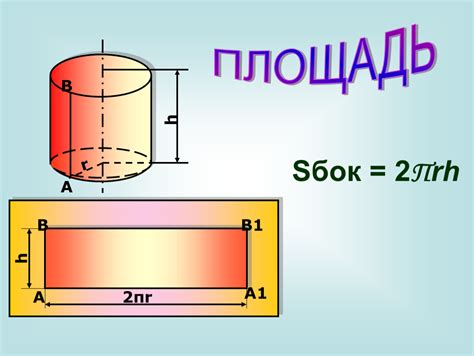
Для определения высоты цилиндра по известной площади боковой поверхности и диаметру необходимо использовать специальную формулу.
Площадь боковой поверхности цилиндра вычисляется по формуле:
S = 2πrh
где S - площадь боковой поверхности, r - радиус основания цилиндра, h - высота цилиндра.
Диаметр цилиндра (d) можно найти, удвоив значение радиуса (r):
d = 2r
Зная значение диаметра (d) и площади боковой поверхности (S), можем выразить радиус основания цилиндра (r) из формулы для площади:
r = S / (2πh)
Подставив значение радиуса в формулу для диаметра (d), получим:
d = 2(S / (2πh))
Выразим высоту цилиндра (h) из полученного уравнения:
h = S / (πd)
Пример
Допустим, у нас есть цилиндр с площадью боковой поверхности S = 100 см² и диаметром d = 10 см. Определим высоту цилиндра по этим данным.
Сначала найдем радиус основания цилиндра (r), подставив значения S и d в формулу:
r = 100 / (2πh) = 100 / (2 * 3.14 * h) ≈ 15.92 / h
Подставим значение радиуса в формулу для диаметра:
10 = 2(15.92 / h) ≈ 31.84 / h
Выразим высоту цилиндра (h) через полученное уравнение:
h ≈ 31.84 / 10 ≈ 3.18 см
Таким образом, высота цилиндра составляет примерно 3.18 сантиметра.
Используя данную формулу, вы сможете определить высоту цилиндра по известным значениям площади боковой поверхности и диаметра.
Что такое цилиндр
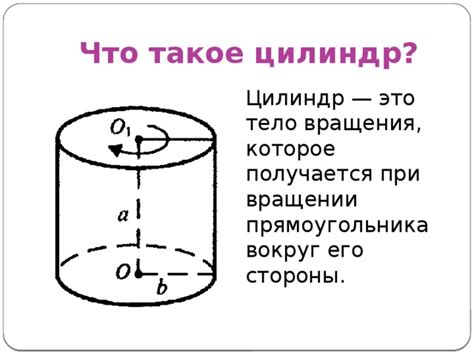
Боковая поверхность цилиндра является выпуклой и ограничена двумя круговыми основаниями, которые лежат на параллельных плоскостях. Расстояние между основаниями называется высотой цилиндра.
Цилиндр является одним из основных геометрических тел и широко применяется в нашей повседневной жизни. Он может быть найден в различных предметах, таких как банки, бутылки, трубы, столбы и т.д. Цилиндрическая форма делает его устойчивым и простым в производстве.
Элементы цилиндра, такие как диаметр, радиус, площадь боковой поверхности и объем, широко используются в различных вычислениях и задачах, связанных с инженерией, архитектурой, физикой и другими науками.
Формула для вычисления площади боковой поверхности цилиндра:
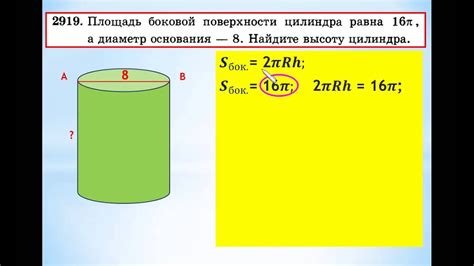
Для того чтобы найти площадь боковой поверхности цилиндра, необходимо знать его радиус основания (r) и высоту (h). Формула для вычисления площади боковой поверхности цилиндра выглядит следующим образом:
S = 2πrh
где S - площадь боковой поверхности цилиндра, π (пи) - математическая константа, равная примерно 3,14159, r - радиус основания цилиндра, h - высота цилиндра.
Используя данную формулу, можно найти площадь боковой поверхности цилиндра по заданным значениям радиуса и высоты.
Выражение для высоты цилиндра через площадь боковой поверхности и диаметр
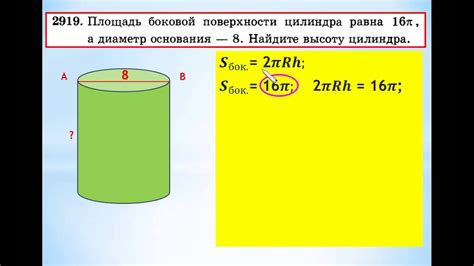
Для нахождения высоты цилиндра по известным площади его боковой поверхности и диаметру существует следующая формула:
| Высота цилиндра (h) | = | 2 * (Площадь боковой поверхности (Sбп)) | / | (Пи (π)) * (Диаметр цилиндра (d)) |
|---|
Таким образом, чтобы найти высоту цилиндра, нужно удвоить площадь его боковой поверхности и разделить на произведение числа π (пи) и диаметра цилиндра.
Перевод формулы в выражение для нахождения высоты цилиндра
Для нахождения высоты цилиндра по известной площади боковой поверхности и диаметру необходимо привести формулу к выражению, которое позволит найти искомую величину.
Площадь боковой поверхности цилиндра вычисляется по формуле:
- S = 2πrh
где S - площадь боковой поверхности, π - математическая константа (приближенное значение равно 3.14159), r - радиус основания цилиндра, h - высота цилиндра.
Для нахождения высоты цилиндра по известным S и D (диаметру основания цилиндра) необходимо воспользоваться формулой, связывающей диаметр и радиус:
- D = 2r
Отсюда можно выразить радиус цилиндра через диаметр:
- r = D/2
Подставив это выражение в исходную формулу, получим:
- S = 2π(D/2)h
Упрощаем:
- S = πDh
И, наконец, выражаем высоту цилиндра:
- h = S/(πD)
Таким образом, получаем выражение для нахождения высоты цилиндра по известной площади боковой поверхности и диаметру:
- h = S/(πD)
Пример вычисления высоты цилиндра по заданным площади и диаметру
Вычисление высоты цилиндра по заданным площади боковой поверхности и диаметру может быть выполнено следующим образом:
- Найдите радиус цилиндра, разделив диаметр на 2.
- Вычислите площадь основания цилиндра, используя формулу площади круга: S = π * r^2, где S - площадь, а r - радиус.
- Вычислите радиус боковой поверхности цилиндра, используя формулу: r_b = √(S_b / π), где S_b - площадь боковой поверхности.
- Найдите высоту цилиндра, используя формулу: h = S_b / (2 * π * r_b).
Итак, чтобы найти высоту цилиндра, следуйте этим шагам:
- Делите диаметр на 2, чтобы найти радиус цилиндра.
- Вычислите площадь основания цилиндра, используя формулу площади круга.
- Найдите радиус боковой поверхности цилиндра, используя формулу.
- Используя площадь боковой поверхности, найдите высоту цилиндра.
При вычислении обратите внимание на единицы измерения, чтобы получить правильный ответ.
Применение полученной высоты цилиндра в практике

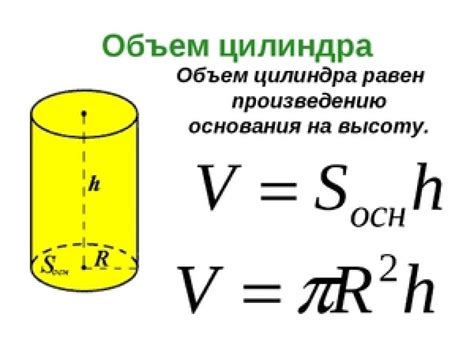
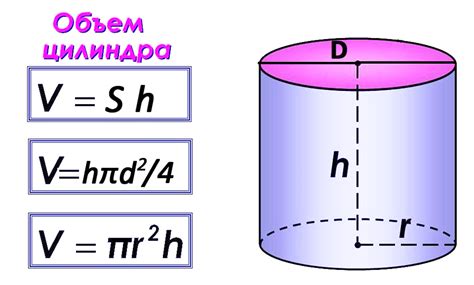
Например, зная высоту цилиндра, можно рассчитать его объем. Формула для расчета объема цилиндра: V = π * r^2 * h, где V - объем, π - число Пи (примерное значение 3.14159), r - радиус основания, h - высота цилиндра. Зная высоту цилиндра, можно применить эту формулу для определения объема цилиндра, что может быть полезным, например, при расчете необходимого объема жидкости для заполнения цилиндрического резервуара.
Также, зная высоту цилиндра, можно рассчитать его площадь основания. Формула для расчета площади основания цилиндра: A = π * r^2, где A - площадь основания, π - число Пи (примерное значение 3.14159), r - радиус основания. Зная высоту цилиндра, можно применить эту формулу для определения площади основания, что может быть полезным, например, при расчете необходимой площади для установки цилиндрического объекта.
Таким образом, полученная высота цилиндра может быть полезной для решения различных практических задач, связанных с расчетами объема и площади основания цилиндра.
Резюме

Для начала найдем радиус цилиндра, разделив диаметр на 2. Затем рассчитаем площадь основания цилиндра, используя формулу площади круга: S = π * r^2, где S - площадь основания, π - математическая константа (приближенное значение 3,14), r - радиус цилиндра.
Далее найдем высоту цилиндра, разделив площадь боковой поверхности на площадь основания: h = Sбп / Sосн, где h - высота цилиндра, Sбп - площадь боковой поверхности, Sосн - площадь основания.
Таким образом, по известным значениям площади боковой поверхности и диаметру можно рассчитать высоту цилиндра, используя соответствующие формулы и математические операции.