Многогранники - это геометрические фигуры, у которых есть грани, вершины и ребра. Они могут быть различных форм и размеров: треугольники, квадраты, призмы, пирамиды и т.д. Одним из важных параметров многогранника является его высота.
Высота многогранника определяется как расстояние между двумя параллельными плоскостями, на которых лежат его основания. Это расстояние можно найти с помощью формулы, которая зависит от типа многогранника.
Например, для прямоугольной призмы, высота может быть найдена по формуле: h = V / A, где V - объем призмы, A - площадь одного из оснований. Для пирамиды, высота вычисляется по формуле: h = (3V) / A, где V - объем пирамиды, A - площадь основания.
Использование формулы для нахождения высоты многогранника

Существует формула, которая позволяет рассчитать высоту многогранника в зависимости от его свойств. Формула может быть различной для разных типов многогранников, таких как прямоугольные параллелепипеды, пирамиды, призмы и другие. Рассмотрим примеры использования формулы для нахождения высоты некоторых многогранников:
| Тип многогранника | Формула для нахождения высоты |
|---|---|
| Прямоугольный параллелепипед | Высота = a, где a - длина одной из ребер основания |
| Пирамида | Высота = (3 * V) / (S_b), где V - объем пирамиды, S_b - площадь основания |
| Призма | Высота = V / S_b, где V - объем призмы, S_b - площадь основания |
Для каждого типа многогранника необходимо знать определенные характеристики, такие как длины ребер, площади основания или объемы. Поэтому перед использованием формулы необходимо провести измерения и рассчитать соответствующие величины.
Использование формул для нахождения высоты многогранника позволяет эффективно решать геометрические задачи и проводить расчеты объемов. Это полезное математическое свойство многогранников, которое находит применение в различных областях науки и инженерии.
Как определить высоту многогранника геометрическими методами
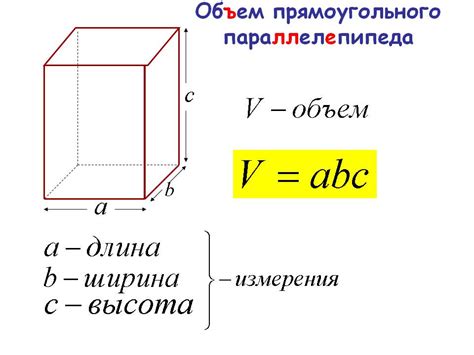
Метод 1: Определение высоты призмы
Если многогранник - призма, то высоту можно найти очень просто. Для этого нужно провести прямую линию, перпендикулярную плоскости основания, и измерить расстояние от вершины до этой линии. Полученное расстояние будет являться высотой призмы.
Метод 2: Определение высоты пирамиды
Если многогранник - пирамида, то высоту также можно найти достаточно просто. Для этого нужно провести прямую линию, перпендикулярную плоскости основания, и измерить расстояние от вершины до этой линии. Полученное расстояние будет являться высотой пирамиды.
Метод 3: Определение высоты многогранника с помощью площадей
Если известны площади поверхности многогранника и площадь одной из его граней, то высоту можно определить следующим образом: высота равна отношению площади поверхности к площади основания.
Метод 4: Определение высоты многогранника с помощью объема
Если известен объем многогранника и площадь одной из его граней, то высоту можно определить следующим образом: высота равна отношению объема к площади основания.
Важно помнить, что эти методы применимы к определению высоты многогранников с правильными гранями и основаниями. Для неправильных многогранников эти методы могут быть неприменимы, и в таких случаях требуется использование более сложных вычислительных методов.
Приложение математических принципов для вычисления высоты многогранника
Если многогранник является прямой призмой, то высота многогранника равна длине отрезка, соединяющего его вершины на основании. Для вычисления высоты прямоугольной призмы используется формула: высота = sqrt(a^2 + b^2), где a и b - длины сторон основания.
Для многогранников без прямых боковых граней, высота может быть вычислена с помощью векторной арифметики. Для этого нужно знать координаты вершин многогранника. Сначала необходимо определить плоскость, содержащую основание многогранника, например, путем взятия трех точек на этом основании. Затем используйте формулу вычисления расстояния от вершины до плоскости, которую можно записать как: высота = |(x - x1, y - y1, z - z1)·n|/|n|, где (x, y, z) - координаты вершины, (x1, y1, z1) - точка на плоскости, n - нормаль к плоскости.
Для многогранников с прямыми боковыми гранями, высота может быть вычислена с использованием теоремы Пифагора для треугольников. Например, для правильного тетраэдра, высота равна h = sqrt(a^2 - (a/2)^2), где a - длина ребра тетраэдра.
В общем случае, для многогранников с произвольными формами, высота может быть вычислена путем разделения многогранника на треугольники и применения теоремы Пифагора к каждому из них. Затем высоты треугольников суммируются для получения итоговой высоты многогранника.
В итоге, для вычисления высоты многогранника необходимо учитывать его форму, основания и вершины. С помощью различных математических принципов и формул можно определить высоту многогранника и использовать это понятие для дальнейших расчетов и анализа.
Примеры вычисления высоты многогранника с использованием формулы
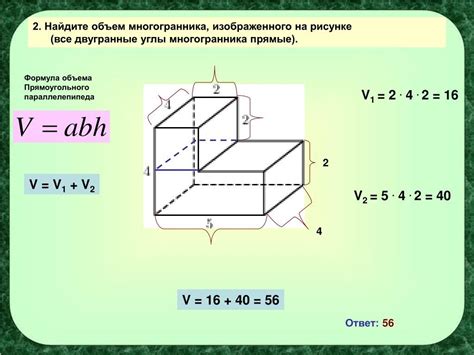
Рассмотрим несколько примеров вычисления высоты различных многогранников с использованием соответствующих формул.
| Многогранник | Формула высоты | Пример вычислений |
|---|---|---|
| Параллелепипед | h = V / (a * b) | Для параллелепипеда с объемом V = 240 и площадью основы a * b = 60 высота равна h = 240 / 60 = 4 |
| Пирамида | h = (3 * V) / (a * b) | Для пирамиды с объемом V = 180 и площадью основы a * b = 30 высота равна h = (3 * 180) / 30 = 18 |
| Цилиндр | h = V / (π * r^2) | Для цилиндра с объемом V = 576 и радиусом основы r = 6 высота равна h = 576 / (π * 6^2) ≈ 4.83 |
В этих примерах формулы используются для нахождения высоты многогранника на основе известных значений объема, площади основы и других параметров. При вычислениях важно учитывать единицы измерения и правильно применять соответствующие формулы.
Задачи на вычисление высоты многогранника из реальной практики

- Определение объема многогранного контейнера. Если известны площади оснований и высота, то по формуле V = S * h можно вычислить объем контейнера. Это может быть полезно при планировании транспортировки или хранении грузов.
- Расчет объема неоднородного тела. Некоторые многогранники могут иметь различные материалы на разных гранях. Вычисление объема такого тела позволяет определить его массу или объем каждого материала.
- Определение площади поверхности многогранника. Высота многогранника используется в формулах для расчета площади его боковой поверхности, как, например, в формуле для площади поверхности прямоугольного параллелепипеда: S = 2 * (a * b + a * h + b * h).
- Построение трехмерных моделей. В технической графике и архитектуре часто используются многогранники для создания трехмерных моделей объектов. Знание высоты многогранника помогает корректно отобразить его на рисунке или в 3D-моделировании.
- Определение высоты объектов на местности. В геодезии и картографии высота многогранника может быть использована для измерения высоты гор, зданий, мостов и других объектов.
Все эти задачи требуют умения правильно вычислять высоту многогранника по известным данным или находить ее вместе с другими характеристиками. Знание формулы для расчета высоты многогранника является важным инструментом для решения практических задач в различных областях.