Пирамиды привлекают внимание своей уникальной формой и загадочной историей. Однако, насколько мы знаем, мало кто думает о том, как рассчитать высоту пирамиды. Чтобы узнать высоту пирамиды, не обязательно отправляться на экспедицию и проводить сложные измерения. В этой статье мы рассмотрим простой метод, позволяющий определить высоту пирамиды по известному объему.
Объем пирамиды - это количество пространства, занимаемого пирамидой. Изучая геометрию, мы узнаем, что объем пирамиды можно вычислить, умножив площадь основания на высоту и разделив полученное значение на 3. Именно эта формула позволяет нам рассчитать объем, если известны площадь основания и высота.
Однако, в нашем случае, у нас уже есть известный объем пирамиды, поэтому нам необходимо найти высоту. Для этого мы преобразуем формулу и изолируем высоту. Сначала умножим обе стороны на 3, а затем разделим на площадь основания. Полученное значение будет представлять высоту пирамиды.
Как восстановить высоту пирамиды по объему

Восстановление высоты пирамиды по известному объему может быть важной задачей при археологических и исследовательских работах. Для решения этой задачи мы можем использовать формулу объема пирамиды и следующие шаги:
| Шаг | Описание |
|---|---|
| 1 | Изучите информацию о пирамиде, включая ее план и основные размеры. |
| 2 | Определите форму пирамиды. Возможно, это будет пирамида с прямоугольным основанием, треугольной или другой формы. |
| 3 | Используя формулу объема пирамиды, выразите высоту пирамиды через известные параметры. Формула для пирамиды с прямоугольным основанием: V = (1/3) * S * h, |
| 4 | Подставьте известные значения в формулу и решите уравнение для высоты пирамиды. |
| 5 | Вычислите значение высоты пирамиды и округлите его до нужной точности, учитывая единицы измерения. |
Именно так можно восстановить высоту пирамиды по известному объему. Помните, что точность результатов может зависеть от точности замеров и предоставленной информации о пирамиде.
История пирамидостроения

Вначале пирамиды были небольшими структурами, созданными для хранения царских усыпальниц. Однако со временем они стали служить символом власти фараонов и приобретали все более грандиозные размеры. Самая известная пирамида - пирамида Хеопса в Гизе, высотой более 140 метров - была построена около 2580 года до нашей эры и считается одной из семи чудес древнего мира.
Строительство пирамид требовало огромных ресурсов и организационного мастерства. Рабочим предстояло перевозить огромные каменные блоки и складывать их в сложные структуры. Инженеры и архитекторы создавали инновационные подъемные механизмы и использовали точные математические расчеты для обеспечения стабильности и прочности пирамид.
Многие пирамиды были разграблены и разрушены веками, но их величественные развалины все равно впечатляют и интересуют ученых и туристов со всего мира. История пирамидостроения свидетельствует о величии и сложности древних культур и оставляет нас с вопросами о технологических и инженерных достижениях тех времен.
Математический подход

Для вычисления высоты пирамиды по ее объему существует математическая формула, которая может быть использована.
Для этого необходимо знать объем пирамиды, который можно вычислить, используя следующую формулу:
| Формула | Описание |
|---|---|
| V = (1/3) * S * h | Объем пирамиды (V) равен одной трети произведения площади основания (S) на высоту (h) |
Для вычисления высоты пирамиды (h) по известному объему (V) и площади основания (S) необходимо переупорядочить формулу:
| Формула | Описание |
|---|---|
| h = (3 * V) / S | Высота пирамиды (h) равна трехкратному произведению объема (V) на обратное значение площади основания (S) |
Таким образом, подставив известные значения объема и площади основания пирамиды в данную формулу, можно получить ее высоту.
Способы измерения объема
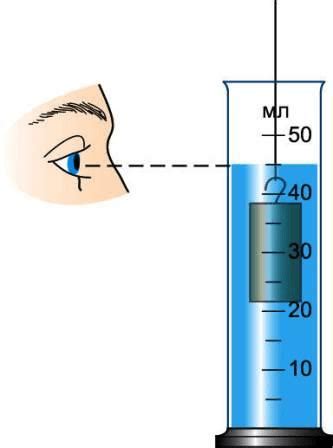
Существует несколько способов измерения объема пирамиды:
- Метод геометрического измерения. Для этого способа необходимо знать форму пирамиды и ее размеры. Объем пирамиды может быть вычислен по формуле, соответствующей ее геометрической форме.
- Метод гидростатического измерения. Этот метод основан на законе Архимеда, который утверждает, что погруженное в жидкость тело теряет вес, равный весу вытесненной им жидкости. Для измерения объема пирамиды по этому методу необходимо погрузить ее в специально подобранную жидкость и измерить изменение ее веса.
- Метод дисплейного измерения. Этот метод использует особое устройство, называемое дисплеем, способное отображать объем тела. Пирамида помещается на дисплей, который автоматически осуществляет измерение ее объема.
- Метод разрезания и взвешивания. Этот метод заключается в разрезании пирамиды на части и последующем взвешивании каждой части. Путем сложения масс всех частей можно получить массу всей пирамиды, а затем с использованием плотности материала пирамиды вычислить ее объем.
Каждый из этих способов имеет свои особенности и может быть применим в зависимости от условий измерения объема пирамиды.
Определение формы пирамиды
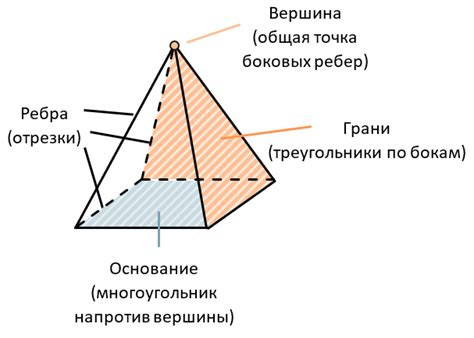
Основания пирамиды могут быть различной формы: квадрат, прямоугольник, треугольник, круг и другие. Из основания выходят боковые грани, которые сходятся в вершине пирамиды.
Важными характеристиками формы пирамиды являются:
| Характеристика | Описание |
| Высота | Расстояние от основания до вершины пирамиды |
| Боковая грань | Грань, образованная боковым ребром и частью основания |
| Угол наклона | Угол между боковой гранью и основанием пирамиды |
Форма пирамиды определяется взаимным расположением ее граней и основания, углами наклона боковых граней и высотой. Зная форму основания и объем пирамиды, можно рассчитать ее высоту с помощью соответствующих формул и математических операций.
Расчет высоты пирамиды
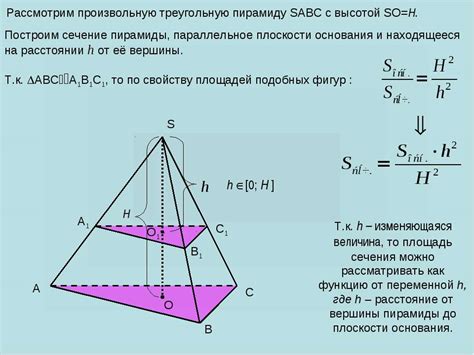
Для рассчета высоты пирамиды по её объему необходимо знать площадь основания:
1. Найдите значение объема пирамиды, используя формулу: V = (1/3) * S * h, где V - объем пирамиды, S - площадь основания, h - высота пирамиды.
2. Зная значение объема V и площадь основания S, можно рассчитать высоту пирамиды следующим образом:
h = (3 * V) / S.
Пример:
| Параметр | Значение |
|---|---|
| Объем пирамиды (V) | 27 м^3 |
| Площадь основания (S) | 9 м^2 |
| Высота пирамиды (h) | (3 * 27) / 9 = 9 м |
Таким образом, высота пирамиды с объемом 27 м^3 и площадью основания 9 м^2 составляет 9 метров.
Примеры применения

1) Архитектура и строительство:
Высота пирамиды играет важную роль при проектировании и строительстве зданий и сооружений. Зная объем пирамиды, архитекторы могут рассчитать высоту и определить необходимые материалы и конструкции для ее строительства.
Например, при проектировании высоких небоскребов архитекторы используют данную формулу для вычисления высоты пирамидальной вершины, чтобы гарантировать безопасность и устойчивость строения.
2) Геодезия и картография:
Высота пирамиды является одним из важных параметров при создании карт и определении рельефа местности. Геодезисты используют формулу для вычисления высоты пиков гор и других неровностей поверхности Земли.
На основе этих данных создаются высотные карты, которые используются в различных отраслях, например, в строительстве, туризме и экологии.
3) Исследования и наука:
Вычисление высоты пирамиды по объему может использоваться при исследовании различных объектов, таких как вулканы, айсберги и скалы. Ученые могут определить высоту и объем этих объектов, что помогает в изучении их свойств и поведения.
Например, с помощью данной формулы геологи могут узнать высоту и объем древних вулканов, что дает информацию об их истории и геологическом развитии.