Прямоугольный треугольник - одна из основных геометрических фигур, которая имеет три стороны и один прямой угол. Он широко используется в различных областях, включая архитектуру, инженерию и геодезию. Полная информация о треугольнике может быть важна для решения задач или выполнения точных измерений.

Одной из основных характеристик треугольника является его высота. Высота относится к отрезку, проведенному из вершины треугольника к основанию в прямом углу. Нахождение высоты прямоугольного треугольника имеет свои особенности и требует знания длины двух его сторон.

Для расчета высоты прямоугольного треугольника можно использовать теорему Пифагора. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы (стороны, противоположной прямому углу) равен сумме квадратов катетов (двух сторон, образующих прямой угол).

Формула для нахождения высоты в прямоугольном треугольнике

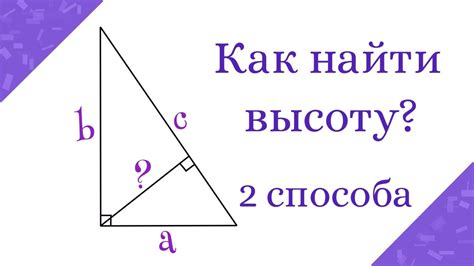
Высота = (Сторона, прилегающая к прямому углу * Сторона, не прилегающая к прямому углу) / Гипотенуза

В данной формуле:

• Сторона, прилегающая к прямому углу - это сторона треугольника, которая является одной из катетов (не гипотенузой).
• Сторона, не прилегающая к прямому углу - это другой катет треугольника (также не гипотенуза).
• Гипотенуза - это наибольшая сторона прямоугольного треугольника, противоположная прямому углу.

Подставляя значения сторон в формулу, можно найти высоту прямоугольного треугольника. Эта формула основана на теореме Пифагора для прямоугольных треугольников.

Пример:

Дано:

• Сторона, прилегающая к прямому углу = 4 см
• Сторона, не прилегающая к прямому углу = 3 см
• Гипотенуза = 5 см

Высота = (4 см * 3 см) / 5 см = 12 см / 5 см = 2.4 см

Таким образом, высота прямоугольного треугольника равна 2.4 см, если даны значения сторон.

Высота прямоугольного треугольника через стороны

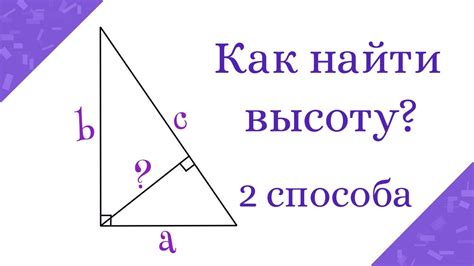
Для нахождения высоты треугольника через стороны можно воспользоваться формулой:

h = (a * b) / c

где h – высота треугольника, a и b – длины катетов (сторон, образующих прямой угол), c – гипотенуза (самая длинная сторона треугольника, противолежащая прямому углу).

Применение этой формулы позволяет легко и быстро найти высоту прямоугольного треугольника через его стороны. Помните, что все стороны треугольника должны быть заданы в одной единице измерения, чтобы получить правильный ответ.

Например, если у вас есть прямоугольный треугольник со сторонами a = 3, b = 4 и c = 5 единиц, то высота треугольника можно рассчитать следующим образом:

h = (3 * 4) / 5 = 12 / 5 = 2.4

Таким образом, высота данного прямоугольного треугольника равна 2.4 единицам.

Используя данную формулу, вы можете рассчитать высоту прямоугольного треугольника через его стороны и получить точное значение этой величины.

Применение формулы в практике

Например, представим себе ситуацию, когда нам нужно определить высоту прямоугольного треугольника, зная длины его двух катетов. С помощью формулы, мы можем легко найти эту высоту и использовать полученные данные для решения различных задач.

В проектировании и строительстве также часто возникают ситуации, где необходимо знание высоты прямоугольного треугольника для корректного расчета различных параметров и размеров.

Применение формулы в практике помогает упростить решение задач, связанных с геометрией, и делает их более доступными для понимания и анализа. Знание этой формулы позволяет производить точные расчеты и измерения, что является важным в различных областях науки и техники.

Пример нахождения высоты треугольника

Предположим, что у нас есть прямоугольный треугольник с известными сторонами a = 5 и b = 12.

Для нахождения высоты треугольника можно воспользоваться формулой:

• Высота треугольника h равна произведению двух катетов и делению результата на гипотенузу.
• h = (a * b) / c,
• где c - гипотенуза треугольника.

В нашем примере:

• a = 5,
• b = 12,
• c - гипотенуза.

Чтобы найти гипотенузу, мы можем воспользоваться теоремой Пифагора:

• c^2 = a^2 + b^2,
• c^2 = 5^2 + 12^2,
• c^2 = 25 + 144,
• c^2 = 169.

Таким образом, гипотенуза равна c = √169 = 13.

Теперь мы можем найти высоту:

• h = (5 * 12) / 13,
• h = 60 / 13,
• h ≈ 4.62.

Таким образом, высота прямоугольного треугольника со сторонами 5 и 12 равна примерно 4.62.