Прямоугольные треугольники являются одними из наиболее интересных и распространенных геометрических фигур. Они имеют две непересекающиеся прямые стороны, которые образуют угол в 90 градусов. Одна из важных характеристик прямоугольного треугольника - это его высота, которая является перпендикулярной к основанию треугольника. В данной статье мы рассмотрим метод нахождения высоты прямоугольного треугольника с использованием известной гипотенузы.
Для начала, давайте вспомним основные сведения о прямоугольном треугольнике. В таком треугольнике одна сторона называется гипотенузой, а две другие - катетами. Гипотенуза является самой длинной стороной, а она противоположна прямому углу. Катеты, в свою очередь, образуют этот самый прямой угол.
Теперь перейдем к основной задаче - нахождению высоты прямоугольного треугольника. Мы знаем, что высота проходит через прямой угол треугольника, значит она является перпендикулярной к основанию. В данном случае, гипотенуза будет служить нам основанием. Теперь нам нужно найти длину высоты.
Определение высоты прямоугольного треугольника
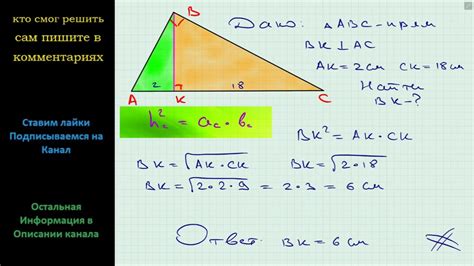
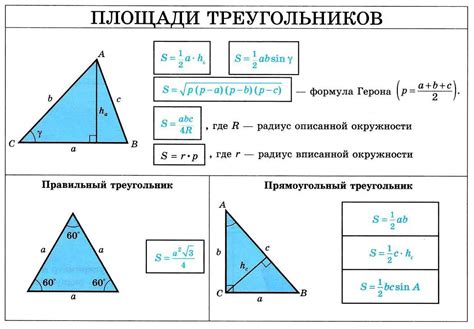
Для определения высоты прямоугольного треугольника используют свойства и формулы геометрии. Одним из способов нахождения высоты является использование длины гипотенузы и основания треугольника.
Для прямоугольного треугольника с гипотенузой c и основанием a или b, высоту h можно найти по следующей формуле:
h = (a * b) / c
Где a и b - длины катетов треугольника, c - длина гипотенузы.
Если известны значения длины гипотенузы и одного из катетов, то эту формулу можно использовать для определения высоты треугольника.
Зная высоту прямоугольного треугольника, можно решить различные задачи и вычисления, связанные с этой фигурой, например, найти площадь треугольника или длины других его сторон.
Определение высоты прямоугольного треугольника является важной задачей в геометрии и находит применение в различных областях, включая строительство, архитектуру, разработку программного обеспечения и другие.
Что такое прямоугольный треугольник?
В прямоугольном треугольнике можно вычислить высоту, используя гипотенузу. Высотой прямоугольного треугольника называется перпендикуляр, опущенный из вершины прямого угла к гипотенузе. Высота является одной из важных характеристик треугольника, так как она позволяет вычислить его площадь.
Что такое гипотенуза?

Гипотенуза связана с другими сторонами треугольника с помощью теоремы Пифагора. Согласно данной теореме, квадрат гипотенузы равен сумме квадратов катетов. Это позволяет найти длину гипотенузы, если известны длины остальных сторон треугольника.
В прямоугольном треугольнике гипотенуза имеет особое значение. Она служит опорой для вычисления высоты треугольника. Высота - это отрезок, проведенный из вершины прямого угла и перпендикулярный гипотенузе. Для нахождения высоты можно использовать теорему Пифагора, зная длину гипотенузы и другую известную сторону треугольника.
| Гипотенуза | Высота |
|---|---|
| 5 | 4 |
| 10 | 8 |
| 13 | 12 |
Таким образом, гипотенуза является важным элементом прямоугольного треугольника, который помогает определить его высоту. Зная длину гипотенузы и другие стороны треугольника, можно легко вычислить его высоту с использованием теоремы Пифагора.
Зачем знать высоту треугольника?

Во-первых, зная высоту треугольника, можно рассчитать его площадь. Формула для вычисления площади треугольника s через его высоту h и основание b выглядит так: s = (h * b) / 2. Понимание, как найти высоту треугольника, позволит вам правильно решать задачи, связанные с расчетами площади.
Во-вторых, высота треугольника может быть использована для нахождения других значений в треугольнике. Например, зная высоту и основание, можно найти длину других сторон или углы, используя соответствующие геометрические связи.
Кроме того, знание высоты треугольника может быть полезным для решения задач геометрического и инженерного характера, например, при проектировании зданий, дорог или других конструкций. Использование высоты треугольника позволяет определить достаточно точные и стабильные значения для расчетов конкретных параметров.
Таким образом, знание высоты прямоугольного треугольника и его применение в различных областях знаний позволяют решать задачи, связанные с вычислениями площади, нахождением других значений в треугольнике и проектированием различных конструкций.
Как найти высоту с помощью гипотенузы?

Когда у нас есть информация о гипотенузе, то есть стороне прямоугольного треугольника, противолежащей прямому углу, мы можем использовать эту информацию для вычисления высоты треугольника.
Для того чтобы найти высоту треугольника с помощью гипотенузы, мы можем использовать следующую формулу:
Высота = (Гипотенуза * Основание) / Гипотенуза
Где "Гипотенуза" - это длина гипотенузы, а "Основание" - это длина стороны прямоугольного треугольника, к которой проведена высота. Подставив значения в формулу, мы сможем вычислить длину высоты треугольника.
Таким образом, зная длину гипотенузы и основания прямоугольного треугольника, вы можете легко найти его высоту, используя данную формулу.
Используем формулу высоты треугольника
Для нахождения высоты прямоугольного треугольника, если известны его гипотенуза и один из катетов, можно использовать следующую формулу:
Высота = (2 * Полупериметр - Гипотенуза) / Катет
Для применения этой формулы необходимо знать длину гипотенузы и одного из катетов треугольника. Полупериметр вычисляется как половина суммы длин всех трех сторон треугольника.
Пример использования формулы:
Пусть у нас есть прямоугольный треугольник с гипотенузой длиной 8 и катетом длиной 6. Мы можем найти высоту, используя формулу:
Высота = (2 * (6 + 8 - 10)) / 6 = (2 * 4) / 6 = 8 / 6 = 1,33
Таким образом, высота прямоугольного треугольника равна приблизительно 1,33. Эта формула позволяет нам расчитать высоту треугольника, используя только длины его сторон.
Пример: нахождение высоты треугольника с известной гипотенузой
Пусть гипотенуза треугольника имеет длину с, а один из катетов - длину a. Для нахождения высоты треугольника воспользуемся формулой:
h = (a * b) / c
где h - высота треугольника, a - длина катета, b - длина второго катета, а c - длина гипотенузы.
Подставляем в формулу известные значения:
h = (a * b) / c
Например, если известно, что гипотенуза треугольника равна 10, а один из катетов равен 6, то подставим значения a = 6, c = 10:
h = (6 * b) / 10
Далее, если известно значение второго катета, можно найти высоту треугольника. Если второй катет, например, равен 8, то:
h = (6 * 8) / 10
h = 48 / 10
h = 4.8
Таким образом, высота треугольника равна 4.8.
Итак, для нахождения высоты прямоугольного треугольника с помощью известной гипотенузы, нам необходимо знать длину гипотенузы и одного из катетов. Подставляем известные значения в формулу и находим значение высоты треугольника.
Важность использования формулы для вычисления высоты треугольника
Высота треугольника - это отрезок, проведенный из вершины треугольника к основанию, перпендикулярно к основанию. Высота прямоугольного треугольника, которая проведена из вершины прямого угла к основанию, имеет особое значение. Она делит треугольник на два прямоугольных треугольника, которые являются подобными треугольниками в отношении стороны, содержащей прямой угол.
Формула для вычисления высоты прямоугольного треугольника по его гипотенузе выглядит следующим образом:
Высота = (Катет1 * Катет2) / Гипотенуза
Где Катет1 и Катет2 - длины катетов прямоугольного треугольника, а Гипотенуза - длина гипотенузы треугольника.
Использование данной формулы позволяет с легкостью вычислять высоту прямоугольного треугольника, что облегчает решение задач, связанных с этими треугольниками. Знание формулы является основой для понимания свойств и особенностей прямоугольных треугольников и их применения в практических задачах.