Высота равнобедренного треугольника – это отрезок, опущенный из вершины перпендикулярно к противоположной стороне. Важно знать, что в равнобедренном треугольнике две стороны равны, а третья сторона, называемая основанием, отличается от них. Найти высоту к боковой стороне можно при помощи простой формулы.
Для вычисления высоты равнобедренного треугольника к боковой стороне необходимы значение длины основания и знание площади фигуры. Соотношение высоты и основания можно выразить формулой: h = (2 * S) / a, где h - высота, S - площадь, а - длина основания. Данная формула дает возможность легко найти высоту равнобедренного треугольника.
Если неизвестна площадь, то можно использовать другую формулу, основанную на свойствах равнобедренного треугольника. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой одновременно. Таким образом, высота равна половине длины основания, то есть h = a / 2.
Высота равнобедренного треугольника: геометрические свойства и способы расчета
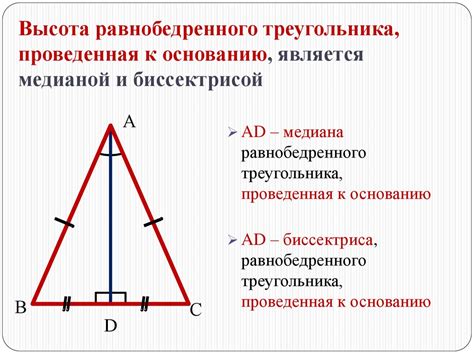
Геометрические свойства равнобедренного треугольника позволяют нам установить следующие законы, связанные с высотой треугольника:
- Высота равнобедренного треугольника является биссектрисой угла, образованного основанием и боковой стороной.
- Высота равнобедренного треугольника делит основание на две равные части.
- Высота равнобедренного треугольника равна медиане, проведенной из вершины, лежащей против основания.
- Высота равнобедренного треугольника является ортогональной диагональю боковой стороны.
Существуют несколько способов расчета высоты равнобедренного треугольника:
- Использование формулы для высоты треугольника, зная длину основания и угол при вершине.
- Использование теоремы Пифагора для расчета длины высоты по длине основания и половине боковой стороны.
- Использование свойств подобных треугольников для нахождения отношений сторон и расчета высоты.
Перед использованием данных способов расчета, необходимо определить известные данные треугольника: длину основания и стороны (боковую сторону или половину боковой стороны).
Зная геометрические свойства равнобедренного треугольника и используя один из способов расчета, вы сможете легко определить высоту треугольника и использовать эту информацию в дальнейших геометрических расчетах и задачах.
Геометрические особенности равнобедренного треугольника и его высота
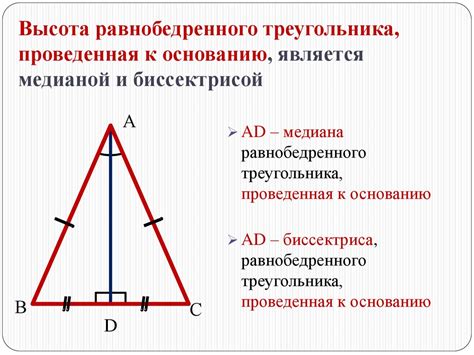
Высота равнобедренного треугольника – это отрезок, проведенный из вершины противоположной основанию, перпендикулярно к основанию треугольника. Заметим, что высота делит основание на две равные части. Важно отметить, что высота равнобедренного треугольника является биссектрисой – линией, разделяющей угол на два равных части.
Изучая геометрические особенности равнобедренного треугольника, мы видим, что высота играет важную роль в его свойствах и вычислениях. Например, зная длину высоты, мы можем найти площадь треугольника по формуле: S = 0.5 * a * h, где a – длина основания, а h – длина высоты.
Также, высота равнобедренного треугольника может использоваться для нахождения других параметров, например, длины боковой стороны. Для этого можно воспользоваться теоремой Пифагора или теоремой косинусов, исходя из известных данных о треугольнике.
Важно отметить, что высота равнобедренного треугольника может быть найдена с использованием таких методов, как построение перпендикуляра или использование геометрических формул. Зная геометрические особенности и свойства равнобедренного треугольника, мы можем легко определить его высоту и использовать ее в различных вычислениях и задачах.