Трапеция -- геометрическая фигура, аналогичная прямоугольнику, но с одной или двумя сторонами, параллельными основаниям, неравными основаниями и двумя неколлинеарными диагоналями. Она встречается во многих задачах геометрии, а понимание ее свойств является важным для решения стандартных геометрических и аналитических задач.
Высота трапеции -- это сегмент перпендикулярный основаниям, разделяющий его на две равные части. Определить высоту трапеции может быть сложной задачей, особенно если нет доступа к точным измерениям и углам. Однако есть простое решение, основанное на использовании окружности, которое позволяет определить высоту с высокой точностью.
Для определения высоты трапеции с окружностью необходимо провести одной из сторон трапеции диаметром окружности. Затем можно определить высоту как расстояние от диаметра до второй стороны трапеции, проходящее через точку касания окружности и этой стороны. При этом, высота будет равна произведению радиуса окружности на синус угла между диаметром и этой второй стороной. Таким образом, достаточно знать только радиус окружности и угол между диаметром и стороной, чтобы определить высоту трапеции с высокой точностью.
Определение высоты трапеции с окружностью: простое решение
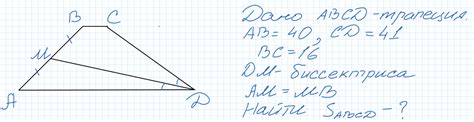
Определение высоты трапеции с окружностью может быть просто, если у вас есть все необходимые данные. Для этого вам понадобится радиус окружности и длины оснований трапеции.
Шаг 1: Вычислите длину диагонали трапеции, с помощью формулы Пифагора. Диагональ равна корню квадратному от суммы квадратов половин оснований: д^2 = (a^2 + b^2), где a и b - длины половин оснований.
Шаг 2: Вычислите длину боковой стороны трапеции, используя найденную в предыдущем шаге диагональ. Длина боковой стороны равна разности диагонали и суммы половин оснований: с = д - (a + b).
Шаг 3: Вычислите высоту трапеции, используя радиус окружности и длину боковой стороны. Высота равна произведению радиуса на длину боковой стороны: h = r * c, где r - радиус окружности, c - длина боковой стороны.
Таким образом, вы можете определить высоту трапеции с окружностью, имея радиус окружности и длины оснований трапеции. Важно помнить, что все измерения должны быть в одной единице измерения.
Трапеция: структура и особенности

Также, трапеция обладает следующими особенностями:
1. У трапеции сумма углов при основаниях равна 180°. Другими словами, углы при основаниях трапеции суммируются в равных прямых углах. Это свойство позволяет использовать трапеции, например, при построении треугольников и параллелограммов.
2. Противолежащие углы трапеции равны. Это означает, что углы, образованные параллельными сторонами трапеции и пересекающими стороной, равны между собой. Такое свойство позволяет быстро находить значения углов в треугольниках, образованных внутри или вокруг трапеции.
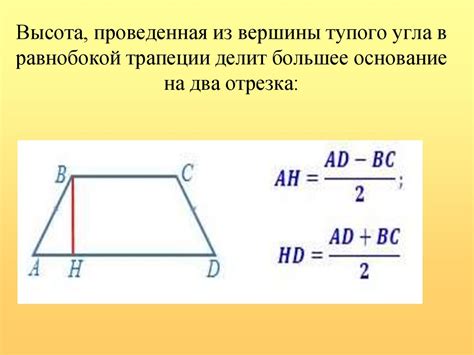
3. Высота трапеции – перпендикуляр, опущенный из верхней стороны на основание. Нахождение высоты трапеции является важной задачей при решении различных геометрических и математических задач. С помощью высоты можно определить площадь трапеции, а также находить другие параметры этой фигуры.
Важно отметить, что существуют различные формулы и способы для определения высоты трапеции. Однако, они зависят от исходной информации и предполагают наличие дополнительных данных о фигуре. В данном тексте рассмотрели одно из простых решений, которое позволяет находить высоту трапеции с окружностью.
Способы определения высоты трапеции

Высоту трапеции можно определить несколькими способами:
1. По основаниям и площади. Если известны длина одного из оснований трапеции и площадь фигуры, то высоту можно найти, используя формулу площади трапеции: H = 2S / (a + b), где H - высота, S - площадь, a и b - длины оснований.
2. По основаниям и боковым сторонам. Если известны длины оснований и боковых сторон трапеции, можно воспользоваться теоремой Пифагора. Сумма квадратов половин суммы длин оснований и разности половин длин боковых сторон равна квадрату высоты: (a + b)² – (c – d)² = H², где H - высота, a и b - длины оснований, c и d - длины боковых сторон.
3. По диагоналям и боковым сторонам. Если известны длины диагоналей и боковых сторон трапеции, то высоту можно найти, используя следующую формулу: H = (2a + 2 Мі)/(b – d), где H - высота, a и b - длины боковых сторон, Мі - половина разности длин диагоналей, d - разность длин оснований.
Выбор метода определения высоты трапеции зависит от доступных данных и условий задачи. Важно правильно интерпретировать известные значения для получения точного результата.
Использование окружности для определения высоты трапеции

Чтобы определить высоту трапеции с помощью окружности, необходимо воспользоваться следующими шагами:
1. Обозначим стороны трапеции следующим образом: основания - а и b, боковые стороны - c и d.
2. Найдем радиус окружности, воспользовавшись формулой r = √(s-a)(s-b)/S, где S - площадь трапеции, a и b - длины оснований, s - полупериметр трапеции.
3. Высота трапеции будет равна 2r, так как радиус окружности является высотой трапеции.
Используя данное решение, можно определить высоту трапеции с окружностью и решить задачи, связанные с этой фигурой.
Простое решение задачи на определение высоты трапеции
Для начала, нам нужно знать радиус окружности, вписанной в трапецию. Обозначим его как r.
Далее, мы можем рассмотреть прямоугольный треугольник, образованный высотой трапеции, радиусом окружности и отрезком прямой, соединяющей центр окружности с одним из углов трапеции.
Используя теорему Пифагора, мы можем записать соотношение:
h2 = r2 - a2
где h - высота трапеции, r - радиус окружности, a - отрезок прямой, соединяющий центр окружности с углом трапеции.
Чтобы найти высоту трапеции, необходимо вычислить значение a и подставить его в формулу.
Простое решение задачи заключается в том, что a можно найти, зная длины оснований трапеции и угол между ними.
То есть, если a - катеты прямоугольного треугольника, а основания трапеции - его гипотенуза, мы можем использовать тригонометрические функции для вычисления значения a.
Зная a, мы можем легко найти h, используя формулу, указанную выше.
Таким образом, простое решение задачи на определение высоты трапеции с окружностью заключается в использовании теоремы Пифагора и тригонометрических функций для нахождения значения высоты. Важно помнить, что перед использованием формулы необходимо знать радиус окружности и длины оснований трапеции.
Примеры решения задачи с использованием окружности

Рассмотрим несколько примеров решения задачи с использованием окружности. Для каждого примера представим таблицу с данными и последовательностью действий для определения высоты трапеции.
| Пример | Исходные данные | Шаги решения | Высота трапеции | |
|---|---|---|---|---|
| Пример 1 | Строны трапеции: a = 5, b = 7, d = 3 | 1. Найти радиус окружности r = d/2 = 3/2 = 1.5 | 2. Найти высоту трапеции h = 2 * sqrt(r^2 - (b - a)^2) | 3. Подставить значения и вычислить h = 2 * sqrt(1.5^2 - (7 - 5)^2) = 2 * sqrt(1.5^2 - 2^2) = 2 * sqrt(2.25 - 4) = 2 * sqrt(2.25 - 4) = 2 * sqrt(-1.75) |
| Пример 2 | Диагонали трапеции: p = 8, q = 6 | 1. Найти радиус окружности r = (p - q) / 2 = (8 - 6) / 2 = 1 | 2. Найти высоту трапеции h = sqrt(r^2 - (p - q)^2/4) | 3. Подставить значения и вычислить h = sqrt(1^2 - (8 - 6)^2/4) = sqrt(1 - 4/4) = sqrt(1 - 1) = sqrt(0) = 0 |
| Пример 3 | Основание и высота трапеции: a = 10, h = 4 | 1. Найти радиус окружности r = sqrt(h^2 + (a/2)^2) = sqrt(4^2 + (10/2)^2) = sqrt(16 + 25) = sqrt(41) | 2. Найти высоту трапеции h = 2 * sqrt(r^2 - (a/2)^2) | 3. Подставить значения и вычислить h = 2 * sqrt(sqrt(41)^2 - (10/2)^2) = 2 * sqrt(41 - 25) = 2 * sqrt(16) = 2 * 4 = 8 |
Таким образом, мы рассмотрели несколько примеров решения задачи с использованием окружности и получили высоту трапеции для каждого случая.