Высота треугольника является одним из важных параметров этой фигуры, ведь она позволяет определить ее площадь. Особенно часто требуется найти высоту треугольника, когда известна длина его основания. Это может потребоваться при решении различных геометрических задач, например, для нахождения площади треугольника или при расчете объемов некоторых фигур.
Как найти высоту треугольника по заданному основанию? Существует простая формула, которая позволяет найти высоту треугольника при известной длине его основания и одной из сторон. Для этого необходимо учитывать, что высота, проведенная из вершины треугольника к его основанию, является перпендикулярной к основанию.
Формула для вычисления высоты треугольника по основанию и одной из сторон выглядит следующим образом: h = (2 * S) / a, где h - искомая высота, S - площадь треугольника, a - длина основания треугольника.
Определение высоты треугольника

Чтобы найти высоту треугольника, можно использовать различные методы:
- Использовать теорему Пифагора для нахождения высоты прямоугольного треугольника. Если известны длины двух катетов, можно применить теорему Пифагора, чтобы найти длину гипотенузы, которая будет являться высотой треугольника.
- Рассмотреть свойство углов треугольника. Если известны углы треугольника, можно использовать тригонометрические функции для нахождения высоты. Например, высоту можно найти по формуле высота = сторона * sin(угол).
- Использовать формулу площади треугольника. Если известны длины всех сторон треугольника, можно использовать формулу площади треугольника и формулу площадь = (основание * высота) / 2, чтобы найти высоту.
В зависимости от доступных данных о треугольнике и поставленной задачи, можно выбрать наиболее подходящий метод для нахождения высоты треугольника.
Способы нахождения высоты треугольника
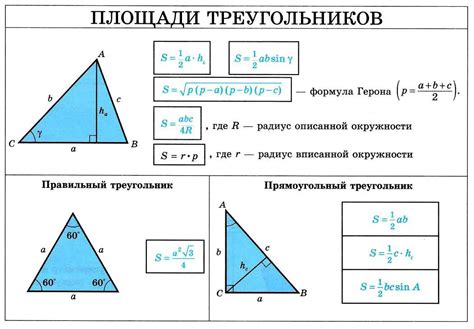
Использование формулы для нахождения площади треугольника и основания:
- Найдите площадь треугольника, используя известные значения его сторон и формулу Герона или другую применимую формулу для треугольника;
- Разделите полученную площадь на длину известного основания треугольника;
- Полученный результат будет равен высоте треугольника относительно этого основания.
Применение теоремы Пифагора:
- Известная основа треугольника должна быть прямой или можно воспользоваться теоремой Пифагора для одного из его прямоугольных подтреугольников;
- Высота треугольника будет являться величиной, противоположной гипотенузе подтреугольника.
Использование тригонометрии:
- Если известны все три стороны треугольника, можно воспользоваться законом синусов или законом косинусов для нахождения одного из его углов;
- Затем можно использовать тригонометрические соотношения между углами и сторонами треугольника для нахождения высоты относительно известной основы.
Применение сходных треугольников:
- Если в треугольнике есть два подобных треугольника, один из которых является прямоугольным, можно использовать их сходство для нахождения высоты треугольника;
- Пропорции соответствующих сторон и высот обоих треугольников помогут найти высоту треугольника относительно его известной основы.
Это лишь некоторые из возможных способов нахождения высоты треугольника. Выбор подходящего метода зависит от доступных данных о треугольнике и условий задачи.
Метод основания и высоты
Для применения метода основания и высоты необходимо знать длину основания (a) и длину высоты (h). Формула для нахождения площади треугольника по основанию и высоте следующая:
- Площадь треугольника (S) = (a * h) / 2
Для нахождения высоты треугольника по основанию и площади, формула будет выглядеть следующим образом:
- Высота треугольника (h) = (2 * S) / a
Метод основания и высоты широко применяется при решении задач геометрии, а также в связанных областях, таких как физика и инженерия. Этот метод позволяет находить высоту треугольника по доступным данным и использовать ее для решения различных задач.
Метод биссектрисы
Для нахождения высоты треугольника с помощью метода биссектрисы необходимо:
- Найти биссектрису треугольника, соответствующую основанию.
- Найти точку пересечения биссектрисы и основания треугольника. Обозначим эту точку как точку D.
- Провести перпендикуляр из точки D к противоположной стороне треугольника. Обозначим точку пересечения перпендикуляра и противоположной стороны как точку E.
- Отрезок DE будет являться искомой высотой треугольника.
Метод биссектрисы является эффективным способом нахождения высоты треугольника, так как он позволяет использовать уже известные свойства биссектрис, что упрощает вычисления и сокращает количество неизвестных величин.
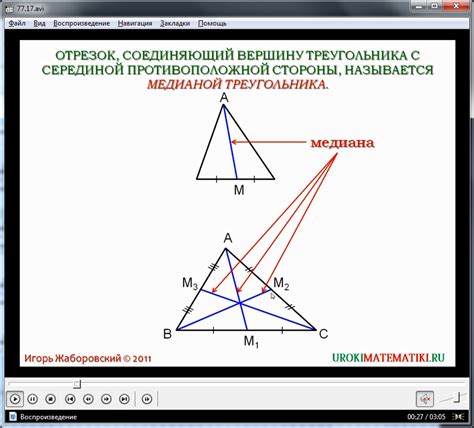
Метод медианы

Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В треугольнике с основанием AB и вершиной C медиана проводится из вершины C до середины основания AB и обозначается MC.
Для определения высоты треугольника по основанию можно воспользоваться следующей формулой:
h = 2/3 * MC
Где h - высота треугольника по основанию, MC - медиана треугольника.
Для использования метода медианы необходимо знать координаты вершин треугольника. Высота найденного треугольника будет равна высоте заданного треугольника.
Метод высоты из вершины
Для нахождения высоты треугольника по основанию по методу высоты из вершины, необходимо знать длину основания и длины двух сторон, образующих основание. Обозначим основание треугольника как AB, где A и B – концы основания, а высоту как h.
Шаги алгоритма поиска высоты треугольника по методу высоты из вершины:
- Изначально выберите одну из вершин треугольника в качестве V.
- Проведите перпендикуляры из вершины V к сторонам основания AB и обозначьте точку пересечения высоты с основанием как H.
- Измерьте длину отрезка HV и это будет значение высоты треугольника.
Данный метод основан на свойстве высоты треугольника – она всегда перпендикулярна основанию и проходит через его середину. Тем самым, проекция треугольника на основание образует прямоугольный треугольник, где одна из сторон является высотой.
Формулы для вычисления высоты треугольника
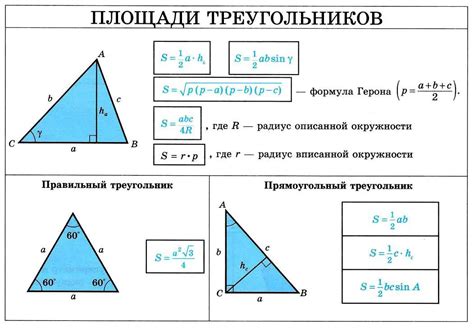
Для нахождения высоты треугольника по основанию можно использовать несколько различных формул, в зависимости от данных, которые у нас имеются.
1. Формула высоты, опущенной на основание треугольника:
| Формула | Описание |
| h = (2 * S) / a | где h - высота треугольника, S - площадь треугольника, a - длина основания треугольника |
2. Теорема Пифагора:
Если известны длины всех сторон треугольника (a, b и c), можно воспользоваться теоремой Пифагора для вычисления высоты треугольника по основанию:
| Формула | Описание |
| h = (a * b) / c | где h - высота треугольника, a, b и c - стороны треугольника |
3. По теореме о высотах треугольника:
Если известны длины сторон треугольника (a, b и c), а также расстояния от вершины до основания (d), можно воспользоваться теоремой о высотах треугольника:
| Формула | Описание |
| h = (2 * S) / c | где h - высота треугольника, S - площадь треугольника, c - длина стороны треугольника, противолежащей высоте (другое название - основание высоты) |
Важно помнить, что в каждой формуле используются разные данные, поэтому нужно знать, какие именно данные у вас есть, чтобы выбрать подходящую формулу для вычисления высоты треугольника.
Формула основания и высоты
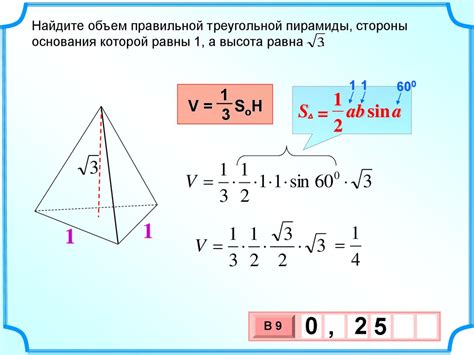
Для нахождения высоты треугольника по основанию можно использовать простую формулу, основанную на знаниях о геометрии. Для этого нужно знать длину основания треугольника.
Формула: чтобы найти высоту треугольника, нужно разделить удвоенную площадь на длину основания:
h = (2 * S) / a
Где:
- h - высота треугольника
- S - площадь треугольника
- a - длина основания треугольника
Эта формула позволяет найти высоту треугольника по известной площади и длине основания. Высота является перпендикуляром, опущенным из вершины треугольника на основание. Используя данную формулу, можно легко рассчитать высоту и решить задачу, связанную с треугольниками.
Формула биссектрисы
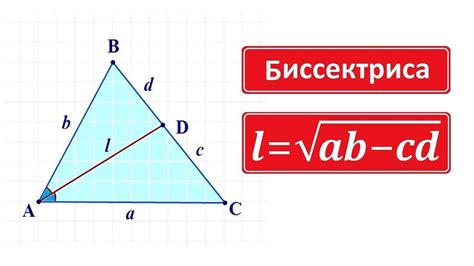
Для применения формулы биссектрисы требуется знать длины сторон треугольника и измерения двух углов, состыкованных с основанием. Если стороны треугольника обозначены a, b и c, а противоположный основанию угол обозначен α, формула биссектрисы запишется следующим образом:
h = 2 * sqrt(b * c * p * (p - a)) / (b + c)
где h - высота треугольника, a - длина основания треугольника, p - полупериметр треугольника.
Зная длину основания и применяя формулу биссектрисы, можно легко определить высоту треугольника. Это особенно полезно при решении задач, связанных с нахождением площади треугольника или построения треугольника по заданным условиям.
Формула медианы
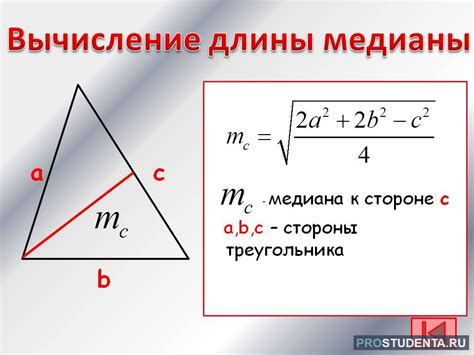
Высота треугольника, проведенная из вершины прямоугольного угла, является частным случаем медианы, так как она также делит основание пополам. Однако общая формула медианы применима к любому треугольнику, независимо от типа его углов.
Формула для вычисления длины медианы задается выражением:
Медиана = 0.5 * √(2b^2 + 2c^2 - a^2)
где a, b и c являются длинами сторон треугольника. Чтобы найти длину медианы, необходимо знать длины всех трех сторон треугольника.
Формула медианы позволяет определить длину этой линии и использовать ее для решения различных геометрических задач, связанных с треугольниками.