Высота треугольника - один из важных параметров этой геометрической фигуры, которая может быть использована при решении различных задач. Одним из способов нахождения высоты является использование радиуса вписанной окружности в треугольник. Узнайте, как по радиусу вписанной окружности рассчитать высоту треугольника и применить эту формулу для решения задач на геометрию!

Для начала, давайте вспомним, что вписанная окружность - это окружность, которая касается всех трех сторон треугольника. Ее радиус обозначается символом r. Если известен радиус вписанной окружности и требуется найти высоту треугольника, используется следующая формула:

h = 2 * r

где h - высота треугольника, а r - радиус вписанной окружности.

Теперь у вас есть простой и эффективный способ найти высоту треугольника, используя радиус вписанной окружности. Не забудьте применить эту формулу при решении задач на геометрию, чтобы быстро и точно получить правильный ответ!

Как определить высоту треугольника по радиусу окружности?

Высота треугольника = 2 * радиус окружности.

Если вам известен радиус вписанной окружности в треугольник, вы можете умножить его на 2, чтобы найти высоту треугольника. Этот способ особенно полезен, когда нужно быстро найти высоту треугольника без заморочек с другими известными значениями.

Обратите внимание, что этот способ работает только для треугольников, в которых окружность вписана и касается всех трех сторон треугольника.

Например, если радиус вписанной окружности в треугольник равен 5 см, то высота треугольника будет равна 10 см (2 * 5 = 10).

Используя данный метод, вы можете легко и быстро найти высоту треугольника по радиусу вписанной окружности без необходимости знания других параметров треугольника.

Рассмотрим треугольник и его радиус вписанной окружности

Для решения задачи по нахождению высоты треугольника по радиусу вписанной окружности необходимо знать, что вписанная окружность делит каждую сторону треугольника на две отрезка, пропорциональных друг другу. Это свойство называется теоремой о вписанной окружности.

Используя теорему о вписанной окружности, можно найти высоту треугольника. Для этого необходимо воспользоваться формулой герона и формулами для нахождения площади треугольника. Зная длины сторон треугольника и радиус вписанной окружности, можно найти площадь треугольника. После этого с помощью формулы для нахождения высоты треугольника по площади можно получить нужное значение.

Зная радиус вписанной окружности треугольника, можно решать различные задачи, например, нахождение длины сторон треугольника, нахождение высоты или углов треугольника. Однако, для нахождения высоты треугольника по радиусу вписанной окружности необходимо провести дополнительные расчеты, используя формулы для площади треугольника и высоты.

Формула для вычисления высоты треугольника по радиусу вписанной окружности

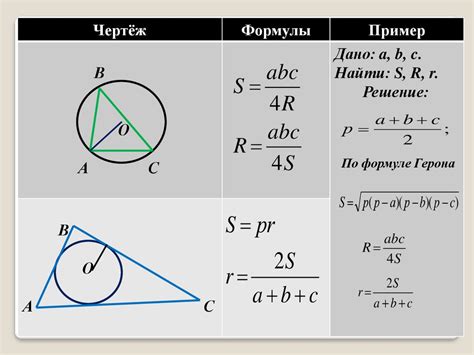
Высота треугольника может быть найдена с использованием радиуса вписанной окружности и длин сторон треугольника. Для вычисления высоты треугольника, мы можем использовать следующую формулу:

h = 2 * r

где h - высота треугольника, а r - радиус вписанной окружности.

Эта формула основана на том факте, что радиус вписанной окружности является перпендикуляром, опущенным из вершины треугольника на противоположную сторону. Высота треугольника является отрезком, соединяющим основание треугольника с вершиной, перпендикулярным к основанию. Поскольку каждая сторона треугольника касается вписанной окружности, она является радиусом этой окружности.

Однако для использования этой формулы необходимо знать радиус вписанной окружности, который можно найти, зная длины сторон треугольника и используя формулу для радиуса вписанной окружности:

r = (a + b + c) / (4 * P)

где a, b и c - длины сторон треугольника, а P - полупериметр треугольника (сумма длин всех сторон, поделенная на 2).

Таким образом, используя формулу для радиуса вписанной окружности, мы можем найти радиус и затем использовать его для вычисления высоты треугольника с помощью первой формулы. Эта формула может быть полезной для решения задач, связанных с треугольниками и вписанными окружностями.