Функции в тригонометрии – это важный раздел математики, который изучает свойства геометрических и алгебраических функций, связанных с углами и их измерением. Одной из ключевых характеристик функции является ее четность или нечетность, которые позволяют определить симметрию графика функции относительно оси координат.
Четность функции означает, что значение функции для отрицательного аргумента будет равно значению функции для соответствующего положительного аргумента. При этом график функции будет симметричен относительно оси ординат. Например, функция синус является нечетной функцией, так как sin(-x) = -sin(x), и график функции симметричен относительно начала координат.
Нечетность функции означает, что значение функции для отрицательного аргумента будет равно отрицанию значения функции для соответствующего положительного аргумента. При этом график функции будет симметричен относительно начала координат. Например, функция косинус является четной функцией, так как cos(-x) = cos(x), и график функции симметричен относительно оси ординат.
Определение четности функции в тригонометрии

Для определения четности функции в тригонометрии необходимо выполнить два шага:
- Выполнить замену аргумента функции на противоположное значение. Если при этом значение функции остается неизменным, то функция является четной. Если значение функции меняется с изменением знака, то функция является нечетной.
- Проверить, выполняется ли для данной функции условие f(x) = f(-x) для всех значений аргумента. Если оно выполняется, то функция является четной. Если условие не выполняется, то функция является нечетной.
Например, для функции синуса (sin(x)) выполняются оба шага:
- При замене аргумента на противоположное значение (sin(-x)) значение функции изменяется с изменением знака, следовательно, функция sin(x) является нечетной.
- Проверка условия f(x) = f(-x) показывает, что sin(x) ≠ sin(-x) для всех значений x, следовательно, функция sin(x) является нечетной.
Таким образом, определение четности функции в тригонометрии позволяет классифицировать функции и упрощает решение уравнений и систем уравнений.
Тригонометрические функции и их графики
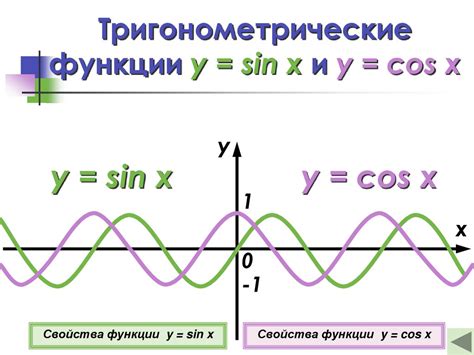
Одной из главных особенностей тригонометрических функций является их периодичность. Все основные тригонометрические функции, такие как синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc), имеют период равный 2π. Это значит, что значения функции повторяются с определенной периодичностью.
Чтобы визуализировать эти функции, можно построить графики, которые позволят наглядно увидеть их поведение. График функции представляет собой набор точек, полученных путем подстановки различных значений аргумента в функцию и отображения полученных значений на координатной плоскости.
Для построения графиков тригонометрических функций можно использовать таблицу значений, где для каждого значений аргумента мы находим соответствующее значение функции. После этого, ставим точку на плоскости, где ось абсцисс представляет значение аргумента, а ось ординат - значение функции.
Для более наглядного представления графиков тригонометрических функций, можно использовать дополнительные инструменты и методы, такие как изменение масштаба осей, рисование сетки и т.д.
| Аргумент (x) | Синус (sin(x)) | Косинус (cos(x)) | Тангенс (tan(x)) |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| π/6 | 1/2 | √3/2 | √3/3 |
| π/4 | √2/2 | √2/2 | 1 |
| π/3 | √3/2 | 1/2 | √3 |
| π/2 | 1 | 0 | ∞ |
Таким образом, графики тригонометрических функций помогают наглядно представить их основные характеристики, такие как периодичность, амплитуда, точки пересечения с осями и другие. Это позволяет лучше понять и изучить поведение этих функций и их взаимодействие в различных контекстах и задачах.
Четность и нечетность функций

Функция называется четной, если она удовлетворяет условию:
f(-x) = f(x)
Это означает, что значение функции для отрицательного аргумента равно значению функции для этого же аргумента, но с противоположным знаком. График четной функции всегда симметричен относительно оси OY.
Функция называется нечетной, если она удовлетворяет условию:
f(-x) = -f(x)
Это означает, что значение функции для отрицательного аргумента равно значению функции для этого же аргумента, но с противоположным знаком исходного значения. График нечетной функции всегда симметричен относительно начала координат.
Проверка на четность функции

Для проведения проверки на четность функции, можно построить соответствующую таблицу значений. Для этого выбираются произвольные значения x и вычисляются значения функции f(x). Затем для каждого вычисленного значения f(x) проводится проверка условий: если f(-x) = f(x), то функция четная, если f(-x) = -f(x), то функция нечетная. В иных случаях функция не обладает ни свойствами четности, ни свойствами нечетности.
| x | f(x) | f(-x) |
|---|---|---|
| 0 | f(0) | f(0) |
| a | f(a) | f(-a) |
| -a | f(-a) | f(a) |
Пример:
| x | f(x) | f(-x) |
|---|---|---|
| 0 | 0 | 0 |
| π/2 | 1 | 1 |
| -π/2 | 1 | 1 |
| π | 0 | 0 |
| -π | 0 | 0 |
Исходя из таблицы значений, видно, что значение функции f(x) совпадает со значением функции f(-x) для любого выбранного значения x. Следовательно, данная функция является четной.
Проверка на нечетность функции

- Заменим в функции значение аргумента на противоположное: f(-x).
- Если новая функция f(-x) равна противоположному значению исходной функции f(x), то функция считается нечетной.
Получившаяся проверка на нечетность основана на том, что геометрический вид графика нечетной функции симметричен относительно начала координат. То есть, если мы отразим график функции относительно оси OY (значения y меняют знак), то получим тот же график.
Проверка на нечетность функции может быть полезной при решении математических задач и определении свойств графика функции. Если функция является нечетной, то ее график будет симметричным относительно начала координат.
Примеры определения четности и нечетности функции
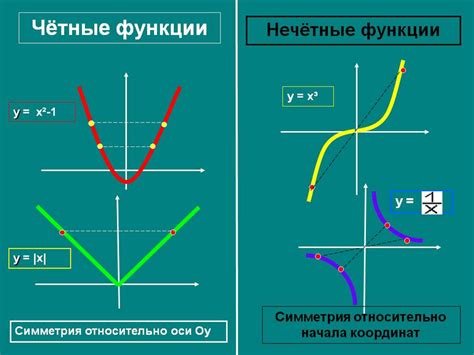
Функция называется четной, если для любого значения аргумента x значение функции f(-x) равно f(x). Иными словами, график четной функции симметричен относительно оси абсцисс. Примером четной тригонометрической функции является косинус: f(x) = cos(x). Для любого значения x выполняется равенство: cos(-x) = cos(x), что подтверждает, что косинус - четная функция.
Функция будет нечетной, если для любого значения аргумента x значение функции f(-x) равно -f(x). Иными словами, график нечетной функции антисимметричен относительно оси абсцисс. Примером нечетной тригонометрической функции является синус: f(x) = sin(x). Для любого значения x выполняется равенство: sin(-x) = -sin(x), что подтверждает, что синус - нечетная функция.
Эти свойства четности и нечетности функции существенно упрощают анализ их графиков и нахождение значений в различных точках. Умение определять четность и нечетность функций позволяет более эффективно работать с тригонометрическими функциями и применять их в различных математических задачах.