У прямоугольного треугольника всегда есть два катета и гипотенуза. Иногда нам нужно найти один из катетов, используя известные значения других сторон. Катеты - это две короткие стороны прямоугольного треугольника, а гипотенуза - самая длинная сторона, противоположная прямому углу.
Существует несколько способов определить длину катета гипотенузы прямоугольного треугольника. Один из самых простых способов - использование теоремы Пифагора. Согласно этой теореме, сумма квадратов длин катетов равна квадрату длины гипотенузы.
Чтобы найти катет, нужно знать длину гипотенузы и другой катет. Подставим известные значения в формулу теоремы Пифагора и решим уравнение относительно неизвестной стороны. Это позволит нам определить длину искомого катета.
Также можно использовать тангенс прямого угла для нахождения длины катета. В прямоугольном треугольнике тангенс угла равен отношению длины катета к длине гипотенузы. Зная значения тангенса и гипотенузы, мы можем выразить длину катета через эти значения и решить уравнение.
Определение понятий

Гипотенуза - самая длинная сторона прямоугольного треугольника, которая находится напротив прямого угла.
Катеты - две меньшие стороны прямоугольного треугольника, которые образуют прямой угол и примыкают к гипотенузе.
Теорема Пифагора - основное математическое утверждение, которое описывает взаимосвязь между сторонами прямоугольного треугольника. Теорема утверждает, что сумма квадратов длин катетов равна квадрату длины гипотенузы.
Гипотенуза прямоугольного треугольника

Гипотенузу прямоугольного треугольника можно вычислить по теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Формула для вычисления гипотенузы выглядит следующим образом:
c = √(a^2 + b^2)
где a и b - длины катетов прямоугольного треугольника. Для вычисления гипотенузы необходимо знать длины обоих катетов.
Гипотенуза прямоугольного треугольника является его наибольшей стороной и является основным элементом для решения задач, связанных с прямоугольными треугольниками. Зная длину гипотенузы, можно вычислить другие стороны и углы треугольника, применяя соответствующие тригонометрические функции.
Таким образом, гипотенуза прямоугольного треугольника играет важную роль при решении геометрических задач, а ее вычисление основано на теореме Пифагора.
Катет
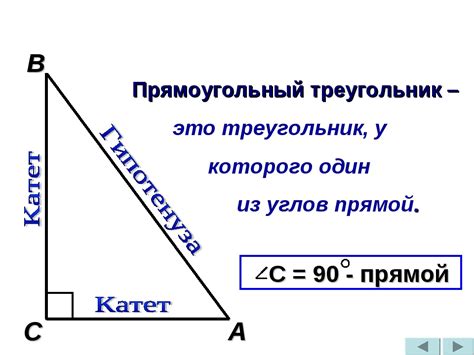
Катеты в прямоугольном треугольнике обладают рядом свойств:
- Длины катетов могут быть любыми числами, в том числе и дробными.
- Сумма квадратов длин катетов равна квадрату длины гипотенузы.
- Катеты всегда меньше гипотенузы.
Чтобы найти значение катета, вам понадобится информация о другом катете и гипотенузе треугольника или о величине углов. Существует несколько методов для вычисления катета.
Один из способов - использование теоремы Пифагора. Если известны длины двух сторон треугольника, можно использовать формулу a^2 + b^2 = c^2, где a и b - катеты, а c - гипотенуза.
Другой способ - использование тригонометрических функций, таких как синус, косинус и тангенс. Если известны длина гипотенузы и значение угла, можно использовать соответствующую тригонометрическую функцию для вычисления катета.
Важно помнить, что точное значение катета зависит от других сторон и углов треугольника, поэтому для его вычисления необходимо иметь достаточно информации.
Теорема Пифагора

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
| Катет а: | Катет b: | Гипотенуза c: |
| Пусть a = 3 | Пусть b = 4 | Требуется найти c |
| Квадрат катета a2: | Квадрат катета b2: | Квадрат гипотенузы c2: |
| a2 = 32 = 9 | b2 = 42 = 16 | ? |
Используя теорему Пифагора, мы можем вычислить квадрат гипотенузы:
c2 = a2 + b2 = 9 + 16 = 25
Таким образом, чтобы найти гипотенузу c, нужно извлечь квадратный корень из c2:
c = √25 = 5
Таким образом, в прямоугольном треугольнике с катетами длиной 3 и 4, гипотенуза будет равна 5.
Формула нахождения катета гипотенузы
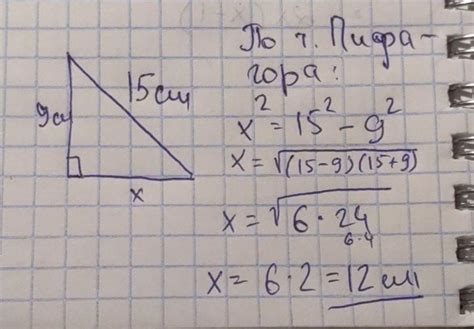
Если известны длина гипотенузы и один из катетов, можно использовать формулу для нахождения второго катета:
- Возвести известный катет в квадрат.
- Возвести длину гипотенузы в квадрат.
- Вычесть квадрат известного катета из квадрата гипотенузы.
- Извлечь корень из получившегося значения.
Формула для нахождения второго катета выглядит следующим образом:
a = sqrt(c² - b²)
где a - длина второго катета, c - длина гипотенузы, b - длина известного катета.
Используя эту формулу, можно легко найти длину второго катета прямоугольного треугольника при известной длине гипотенузы и одном из катетов.
Примеры решения

Пример 1:
Дан прямоугольный треугольник с гипотенузой длиной 5 и одним катетом равным 3. Найдем второй катет.
Используем формулу Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
5^2 = 3^2 + x^2
25 = 9 + x^2
x^2 = 16
x = 4
Ответ: второй катет равен 4.
Пример 2:
Дан прямоугольный треугольник с гипотенузой длиной 13 и одним катетом равным 5. Найдем второй катет.
Используем формулу Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
13^2 = 5^2 + x^2
169 = 25 + x^2
x^2 = 144
x = 12
Ответ: второй катет равен 12.
Пример 3:
Дан прямоугольный треугольник с гипотенузой длиной 17 и одним катетом равным 8. Найдем второй катет.
Используем формулу Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
17^2 = 8^2 + x^2
289 = 64 + x^2
x^2 = 225
x = 15
Ответ: второй катет равен 15.
Пример 1

Рассмотрим пример нахождения катета гипотенузы прямоугольного треугольника. Допустим, известны длина гипотенузы и другого катета.
Пусть длина гипотенузы равна 5 сантиметров, а длина другого катета равна 4 сантиметра. Найдем длину недостающего катета.
Для этого воспользуемся теоремой Пифагора:
| Гипотенуза: | Катет 1: | Катет 2: |
| c = 5 см | a = ? | b = 4 см |
Теорема Пифагора утверждает, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы:
a2 + b2 = c2
Подставим известные значения:
a2 + 42 = 52
a2 + 16 = 25
Выразим a:
a2 = 25 - 16
a2 = 9
Извлечем квадратный корень:
a = √9
a = 3 см
Таким образом, длина недостающего катета равна 3 сантиметрам.
Пример 2

Предположим, что мы знаем значение гипотенузы и одного катета прямоугольного треугольника, и хотим найти значение второго катета.
Рассмотрим следующую ситуацию: гипотенуза прямоугольного треугольника равна 10, а один из катетов равен 6.
Для решения этой задачи воспользуемся теоремой Пифагора:
квадрат гипотенузы равен сумме квадратов катетов, то есть a² = b² + c², где a - гипотенуза, b и c - катеты.
Подставим известные значения в формулу: 10² = 6² + c²
Выполним вычисления:
| 10² | = | 6² + c² |
|---|---|---|
| 100 | = | 36 + c² |
| 100 - 36 | = | c² |
| 64 | = | c² |
Теперь найдем квадратный корень из обоих сторон уравнения и получим: c = √64 = 8.
Таким образом, второй катет равен 8.