Треугольник – это основной геометрический объект, состоящий из трех линий, называемых сторонами. Один из наиболее важных параметров треугольника – его высота. Как найти высоту треугольника по сторонам? Это вопрос, который часто возникает при решении геометрических задач и которому можно найти ответ с использованием специальной формулы.
Формула для нахождения высоты треугольника по сторонам пригодится как начинающим, так и опытным математикам, ведь она позволяет с легкостью решить самые разнообразные задачи на плоскости.
Для того чтобы найти высоту треугольника, нужно знать длины двух его сторон и какой-либо угол. Тогда используя соответствующую формулу, вы сможете получить точный результат. Один из способов найти высоту треугольника – это применить теорему Пифагора, которая устанавливает связь между длинами сторон треугольника и его высотой.
Определение высоты треугольника

Существует несколько способов определения высоты треугольника:
- Построение высоты с помощью перпендикуляра: Высоту треугольника можно построить, проведя перпендикуляр из вершины к противоположной стороне или ее продолжению. Для этого необходимо найти середину этой стороны и провести перпендикуляр к ней из вершины треугольника.
- Определение высоты по формуле: Высоту треугольника можно определить, используя формулу h = (2 * S) / a, где h - высота треугольника, S - площадь треугольника, a - длина основания треугольника.
- Определение высоты по теореме Пифагора: Если известны длины всех трех сторон треугольника, то высота треугольника может быть найдена с использованием теоремы Пифагора.
Знание высоты треугольника может быть полезно при решении задач по геометрии, нахождении площади треугольника и определении его свойств.
Формула для вычисления высоты
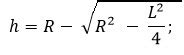
Чтобы найти высоту треугольника по сторонам, можно использовать формулу Герона. Формула Герона позволяет найти площадь треугольника, и высоту можно выразить через эту площадь и длину любой из сторон.
Формула Герона выглядит следующим образом:
S = √(p * (p - a) * (p - b) * (p - c)),
где S - площадь треугольника, a, b, c - длины сторон треугольника, p - полупериметр треугольника, вычисляемый по формуле p = (a + b + c) / 2.
Зная площадь треугольника и длину одной из сторон, можно использовать следующую формулу для нахождения высоты:
h = (2 * S) / a,
где h - высота треугольника, S - площадь треугольника, a - длина стороны треугольника.
Для вычисления высоты треугольника по сторонам необходимо знать длины всех сторон. Подставьте значения в формулы и произведите вычисления, чтобы найти высоту треугольника.
Как найти высоту треугольника с известными сторонами
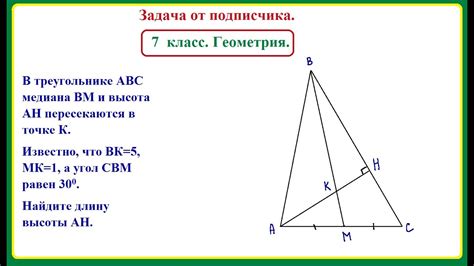
Для нахождения высоты треугольника, когда известны длины его сторон, можно использовать формулу, основанную на теореме Пифагора и площади треугольника.
Если в треугольнике известны стороны a, b и c, то высоту h можно найти с помощью следующей формулы:
| Высота треугольника h равна: | h = 2 * (Площадь треугольника / Сторона c) |
Для вычисления площади треугольника можно использовать формулу Герона:
| Площадь треугольника равна: | Площадь = √(p * (p - a) * (p - b) * (p - c)), |
| где p - полупериметр треугольника, равный (a + b + c) / 2. |
Например, если в треугольнике известны стороны a = 5, b = 12 и c = 13, то для нахождения высоты h нужно:
- Вычислить полупериметр треугольника:
- Вычислить площадь треугольника:
- Вычислить высоту треугольника:
| p = (a + b + c) / 2 | = (5 + 12 + 13) / 2 | = 30 / 2 | = 15 |
| Площадь = √(p * (p - a) * (p - b) * (p - c)) | = √(15 * (15 - 5) * (15 - 12) * (15 - 13)) | = √(15 * 10 * 3 * 2) | = √(900) | = 30 |
| h = 2 * (Площадь / Сторона c) | = 2 * (30 / 13) | = 2.308 |
Таким образом, высота треугольника с известными сторонами a = 5, b = 12 и c = 13 равна примерно 2.308.
Используя данную формулу, вы можете находить высоту треугольника, зная его стороны в любых единицах измерения.
Нахождение высоты треугольника через площадь
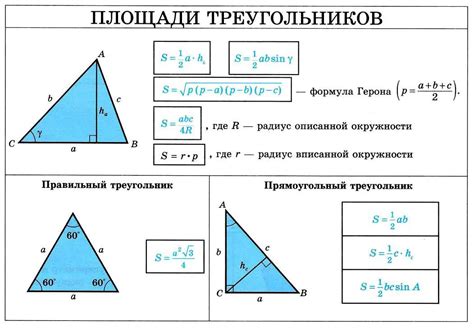
Высота треугольника может быть найдена различными способами, и один из них - через площадь треугольника. Если известна площадь треугольника и длина основания (одной из сторон), можно использовать следующую формулу:
Высота треугольника = (2 * Площадь треугольника) / Длина основания
При использовании этой формулы важно учесть, что единицы измерения площади и длины основания должны быть одинаковыми.
Давайте рассмотрим пример. Предположим, у нас есть треугольник со стороной базы, равной 6 см, и площадью, равной 12 квадратных см. Чтобы найти высоту треугольника, мы можем воспользоваться формулой:
Высота треугольника = (2 * 12 кв. см) / 6 см = 4 см
Таким образом, высота треугольника равна 4 см.
Нахождение высоты треугольника через площадь - это полезный метод, который позволяет определить высоту треугольника с помощью известных данных о площади и длине основания. Этот метод находит широкое применение не только в геометрии, но и в других областях, где требуется рассчитать высоту фигуры.
Пример вычисления высоты треугольника
Рассмотрим пример вычисления высоты треугольника по формуле. Пусть у нас есть треугольник ABC, с известными значениями сторон a, b и c.
Сначала найдем полупериметр треугольника, который вычисляется по формуле:
s = (a + b + c) / 2
Далее используем формулу для нахождения площади треугольника:
S = √(s * (s - a) * (s - b) * (s - c))
Где S - площадь треугольника.
Чтобы найти высоту треугольника, можно использовать следующую формулу:
h = (2 * S) / a
Где h - высота треугольника, а a - сторона, к которой проводится высота.
Подставляя известные значения, мы можем вычислить высоту треугольника. Например, пусть a = 5, b = 12 и c = 13. Подставляем значения в формулу:
| Сторона | Значение |
|---|---|
| a | 5 |
| b | 12 |
| c | 13 |
Вычисляем полупериметр:
s = (a + b + c) / 2 = (5 + 12 + 13) / 2 = 30 / 2 = 15
Вычисляем площадь треугольника:
S = √(s * (s - a) * (s - b) * (s - c)) = √(15 * (15 - 5) * (15 - 12) * (15 - 13)) = √(15 * 10 * 3 * 2) = √(900) = 30
Вычисляем высоту треугольника:
h = (2 * S) / a = (2 * 30) / 5 = 60 / 5 = 12
Таким образом, высота треугольника ABC равна 12 единицам длины.
Задачи на нахождение высоты треугольника
| № | Условие задачи | Решение |
|---|---|---|
| 1 | Даны стороны треугольника: a = 5 см, b = 12 см, c = 13 см. Найдите высоту треугольника, опущенную на сторону a. | В данной задаче мы можем воспользоваться формулой для нахождения площади треугольника по его сторонам и радиусу вписанной окружности: S = a * ha / 2 = r * p, где ha - высота, опущенная на сторону a, r - радиус вписанной окружности, p - полупериметр треугольника. Известно, что площадь равнобедренного треугольника можно вычислить по формуле S = (b * ha) / 2. Подставим известные значения и найдем высоту ha: (5 * ha) / 2 = 5 * 12 / 2, ha = 12 см. |
| 2 | Даны стороны треугольника: a = 8 см, b = 15 см, c = 17 см. Найдите высоты треугольника, опущенные на стороны a, b и c. | Мы можем воспользоваться формулой Герона для нахождения площади треугольника по его сторонам: S = sqrt(p * (p - a) * (p - b) * (p - c)), где p - полупериметр треугольника. Подставим известные значения и найдем площадь S: p = (a + b + c) / 2 = (8 + 15 + 17) / 2 = 20 см, S = sqrt(20 * (20 - 8) * (20 - 15) * (20 - 17)) = sqrt(20 * 12 * 5 * 3) = 30 см. Зная площадь треугольника и одну из его сторон, мы можем вычислить высоту по формуле ha = (2 * S) / a. Подставим значения и найдем высоты треугольника: ha = (2 * 30) / 8 = 15 / 4 = 3.75 см, hb = (2 * 30) / 15 = 15 / 2 = 7.5 см, hc = (2 * 30) / 17 ≈ 3.53 см. |
| 3 | Даны стороны треугольника: a = 3 см, b = 4 см, c = 5 см. Найдите высоту треугольника, опущенную на сторону c. | Мы можем воспользоваться формулой для нахождения высоты треугольника, опущенной на сторону c: hc = (2 * S) / c, где S - площадь треугольника. По формуле Герона, площадь треугольника равна S = sqrt(p * (p - a) * (p - b) * (p - c)), где p - полупериметр треугольника. Подставим известные значения и найдем площадь S: p = (a + b + c) / 2 = (3 + 4 + 5) / 2 = 6 см, S = sqrt(6 * (6 - 3) * (6 - 4) * (6 - 5)) = sqrt(6 * 3 * 2 * 1) = sqrt(36) = 6 см. Подставим значения и найдем высоту треугольника: hc = (2 * 6) / 5 = 12 / 5 = 2.4 см. |
Это только некоторые примеры задач на нахождение высоты треугольника. В каждой задаче можно использовать различные формулы и методы решения, в зависимости от известных данных и требуемого результата. Важно хорошо знать основы геометрии и уметь применять их на практике.
Важные моменты при расчете высоты треугольника
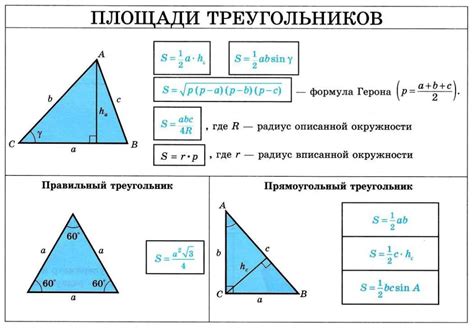
Для расчета высоты треугольника, необходимо учитывать несколько важных моментов. Во-первых, высота треугольника проводится из вершины до противоположной стороны, перпендикулярно этой стороне. Таким образом, высота образует прямой угол с этой стороной.
Во-вторых, для расчета высоты треугольника вам может потребоваться знание длин других сторон. Обычно это одна из сторон треугольника и известна как основание. Основание обозначается буквой "b". Для определения высоты треугольника по стороне применяется следующая формула:
h = (2 * S) / b
где "h" - высота треугольника, "S" - площадь треугольника, "b" - длина основания.
Иногда могут быть известны длины всех сторон треугольника, и, таким образом, основание может быть неопределенным. В этом случае, можно определить высоту треугольника с помощью формулы Герона.
Важно помнить, что в треугольниках с различными типами, например, прямоугольных или равносторонних треугольниках, существуют специальные формулы для расчета высоты.
При решении задач, связанных с нахождением высоты треугольника, важно учитывать все эти моменты и выбирать подходящую формулу в зависимости от известных данных.