Обратная матрица - это особая матрица, при умножении которой на исходную матрицу получается единичная матрица. Нахождение обратной матрицы является важной задачей в линейной алгебре и находит широкое применение в различных областях, таких как физика, экономика и компьютерная графика.
Один из популярных методов нахождения обратной матрицы - метод Гаусса. Этот метод позволяет привести исходную матрицу к ступенчатому виду с помощью элементарных преобразований. Затем, используя обратные элементарные преобразования, можно получить обратную матрицу.
Для того чтобы найти обратную матрицу 3х3 с единичной матрицей, необходимо выполнить ряд шагов. Сначала составим расширенную матрицу, где исходная матрица будет находиться слева от черты, а справа будет находиться единичная матрица. Затем применим элементарные преобразования, пока исходная матрица не примет вид единичной матрицы, а справа от черты не получим обратную матрицу.
Что такое обратная матрица?

Обратная матрица существует только для квадратных матриц, то есть матриц, у которых количество строк равно количеству столбцов. В этом руководстве мы сосредоточимся на нахождении обратной матрицы для трёхмерных квадратных матриц размером 3x3.
Обратная матрица находит применение во множестве прикладных задач, таких как решение систем линейных уравнений, поиск обратного преобразования, вычисление определителя матрицы и многое другое.
Для матрицы A, обратная матрица обозначается как A-1. Вычисление обратной матрицы может быть непростой задачей, но с помощью определенных алгоритмов и методов, мы можем эффективно находить обратные матрицы.
Далее мы рассмотрим простое руководство, как найти обратную матрицу размером 3x3 с единичной матрицей, используя метод Гаусса-Жордана.
Шаг 1: Определение 3x3 единичной матрицы
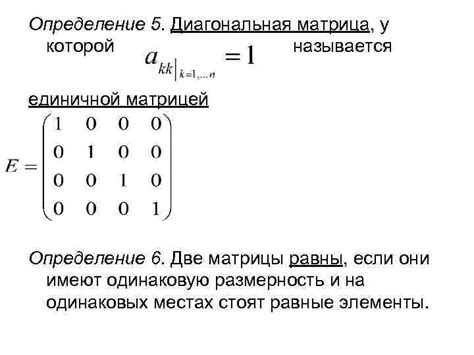
Единичная матрица, обозначаемая как I, представляет собой квадратную матрицу, у которой на главной диагонали (от верхнего левого угла до нижнего правого угла) стоят единицы, а все остальные элементы равны нулю.
В случае 3x3 единичной матрицы, она выглядит следующим образом:
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Каждый элемент на главной диагонали равен 1, а все остальные элементы равны 0.
Распознавание и понимание единичной матрицы важны для нахождения обратной матрицы, так как часть процесса заключается в выражении обратной матрицы через элементы исходной единичной матрицы.
Что такое 3x3 единичная матрица?

Единичная матрица играет важную роль в линейной алгебре и матричных операциях. Она является нейтральным элементом относительно умножения и сложения матриц. Для любой матрицы A размером 3 на 3 выполнено условие I × A = A и A + I = A.
Единичная матрица также используется при поиске обратной матрицы. Если матрица A имеет обратную матрицу A-1, то A × A-1 = I.
Таким образом, понимание 3x3 единичной матрицы важно при выполнении различных операций с матрицами, таких как умножение, сложение и нахождение обратной матрицы.
Шаг 2: Формула для расчета обратной матрицы 3x3 с единичной матрицей

Обратная матрица 3x3 с единичной матрицей может быть рассчитана по следующей формуле:
Пусть A - исходная матрица размером 3x3, а A-1 - обратная матрица. Тогда обратная матрица может быть найдена с использованием следующей формулы:
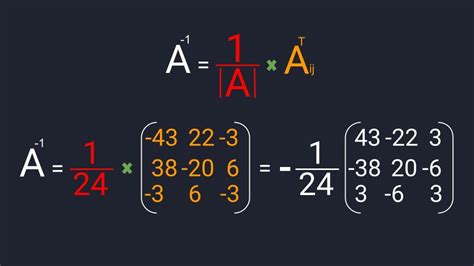
A-1 = (1/|A|) * adj(A)
Где |A| обозначает определитель матрицы A, а adj(A) - матрица алгебраических дополнений матрицы A.
Для нахождения обратной матрицы сначала необходимо рассчитать определитель матрицы A. Затем, используя алгебраические дополнения, формируется матрица adj(A). После этого, adj(A) умножается на обратное значение определителя матрицы A для получения итоговой обратной матрицы A-1.
Эта формула позволяет найти обратную матрицу 3x3 с единичной матрицей для данных значений матрицы A.
Как использовать формулу для расчета?

Для нахождения обратной матрицы 3x3 с единичной матрицей можно использовать формулу. Следуйте этим шагам:
- Найдите определитель исходной матрицы 3x3. Для этого раскройте скобки и вычислите сумму произведений элементов, умноженных на их алгебраические дополнения. Определитель может быть как положительным, так и отрицательным.
- Транспонируйте матрицу, заменив элементы на их соответствующие алгебраические дополнения. Алгебраическое дополнение элемента - это определитель минора, умноженный на -1 в степени суммы индексов элемента.
- Найдите обратный определитель, вычислив обратное значение определителя исходной матрицы. Обратный определитель обозначается как 1/определитель.
- Умножьте транспонированную матрицу на обратный определитель, чтобы получить обратную матрицу.
Теперь вы знаете, как использовать формулу для расчета обратной матрицы 3x3 с единичной матрицей.
Шаг 3: Пример расчета обратной матрицы 3x3 с единичной матрицей
Для наглядного понимания процесса нахождения обратной матрицы 3x3 с единичной матрицей, рассмотрим конкретный пример.
Пусть у нас есть исходная матрица A:
1 2 3
0 1 4
5 6 0
Сначала мы добавим к ней единичную матрицу:
1 2 3 | 1 0 0
0 1 4 | 0 1 0
5 6 0 | 0 0 1
Затем применим элементарные преобразования строк с помощью метода Гаусса-Жордана, чтобы привести исходную матрицу к форме единичной матрицы:
1 0 0 | -4 -3 2
0 1 0 | 5 3 -2
0 0 1 | 1 2 -1
В результате получаем обратную матрицу A-1:
-4 -3 2
5 3 -2
1 2 -1
Таким образом, обратная матрица 3x3 с единичной матрицей для исходной матрицы A равна:
-4 -3 2
5 3 -2
1 2 -1
Теперь мы можем использовать обратную матрицу для решения линейных уравнений, вычисления определителя и других задач.
Расчет шаг за шагом с пояснениями

- Начните с заданной матрицы размером 3х3, для которой нужно найти обратную матрицу.
- Для этого расширьте заданную матрицу единичной матрицей так, чтобы справа от нее находилась матрица размером 3х3, состоящая только из единиц на главной диагонали. Новая расширенная матрица будет иметь размерность 3х6.
- Примените элементарные преобразования строк, чтобы привести левую часть расширенной матрицы к единичной матрице.
- После преобразования левая часть расширенной матрицы станет единичной, а правая часть будет содержать обратную матрицу искомой матрицы. В таком случае, обратная матрица будет находиться в правой части расширенной матрицы.
- Выделите правую часть расширенной матрицы и она станет обратной матрицей исходной матрицы.
Используя указанные шаги, вы сможете рассчитать обратную матрицу 3х3 с единичной матрицей. Необходимо внимательно следить за элементарными преобразованиями строк, чтобы правильно получить обратную матрицу.