Отношение в процентах является одним из важных понятий в математике и финансах. Это позволяет выразить одно значение в виде процента от другого значения. Нахождение отношения в процентах может быть полезным в различных ситуациях, начиная от финансового планирования до статистического анализа. В этой статье мы рассмотрим 5 способов расчета отношения в процентах.

Первый способ - использование простого правила трех. Здесь необходимо определить три значения: начальное значение (A), конечное значение (B) и процентное отношение (P). Формула выглядит следующим образом: P% = (B - A) / A * 100. Данная формула позволяет найти, насколько процентов одно значение отличается от другого.

Второй способ - использование процентного соотношения. Формула здесь также учитывает три значения: начальное значение (A), конечное значение (B) и процентное соотношение (P%). Формула выглядит следующим образом: B = A * (1 + P%). С помощью этой формулы можно найти конечное значение, учитывая начальное значение и процентное соотношение.

Третий способ - использование процентной формулы. При использовании этой формулы необходимо определить два значения: начальное значение (A) и процентное отношение (P%). Формула выглядит следующим образом: P% = (A * P) / 100. Данная формула позволяет найти, какое значение составляет процент от начального значения.

Четвертый способ - использование процентной разницы. Здесь необходимо определить два значения: начальное значение (A) и конечное значение (B). Формула выглядит следующим образом: P% = ((B - A) / A) * 100. Позволяет найти процентную разницу между двумя значениями.

Пятый способ - использование процентного изменения. Для расчета процентного изменения необходимо определить два значения: начальное значение (A) и конечное значение (B). Формула выглядит следующим образом: P% = ((B - A) / A) * 100. Позволяет найти, на сколько процентов изменилось одно значение относительно другого.

Процент от числа: как найти?

Существует несколько способов нахождения процента от числа:

1. Процент как десятичная доля - процент от числа может быть найден, умножив число на соответствующую десятичную долю процента. Например, чтобы найти 20% от числа 100, нужно умножить 100 на 0.2.
2. Процентная доля от 100% - в этом случае нахождение процента от числа сводится к нахождению процентной доли числа от 100%. Например, чтобы найти 15% от числа 200, нужно найти 15% от 100 и умножить на 2.
3. Использование пропорции - установление пропорционального соотношения между числом и его процентом, и нахождение недостающего значения. Например, если известно, что 25% это 50, то чтобы найти 20%, нужно найти такое число x, чтобы отношение 20 к x было такое же, как отношение 25 к 50.
4. Процент от суммы нескольких чисел - в некоторых задачах требуется найти процент от суммы нескольких чисел. В этом случае находится процент от каждого числа и суммируются полученные значения.
5. Использование калькулятора - для удобства и быстроты расчетов можно воспользоваться калькулятором. Многие современные калькуляторы имеют функцию расчета процента от числа.

Независимо от выбранного способа, важно помнить о том, что процент от числа представляет собой долю от этого числа. Правильное использование и понимание расчета процента поможет в решении различных задач и упростит работу с числами.

Первый способ расчета процента от числа

Расчет процента от числа можно выполнить с использованием первого способа, который заключается в умножении числа на процент и делении полученного значения на 100.

Для примера, если необходимо найти 20% от числа 500, нужно умножить 500 на 20 и разделить результат на 100:

20% от 500 = (500 * 20) / 100 = 100

Таким образом, 20% от числа 500 равно 100.

Второй способ расчета процента от числа

Если вам нужно найти процент от числа, можно воспользоваться вторым способом расчета. Он заключается в использовании формулы:

Процент от числа = (Процент / 100) * Число

Чтобы применить эту формулу, нужно начать с расчета десятичной дроби от процента. Для этого делите процент на 100. Затем умножьте полученную десятичную дробь на число, чтобы найти процент от числа.

Например, если нужно найти 20% от числа 1000, сначала разделите 20 на 100, получив 0.2. Затем умножьте 0.2 на 1000, чтобы получить 200. Таким образом, 20% от числа 1000 равно 200.

Этот способ расчета может быть полезен в различных ситуациях, например, при расчете скидки, налога или процентного прироста.

Процент относительно другого значения: как найти?

1. С помощью простого правила трех. Для расчета процента относительно другого значения с использованием простого правила трех нужно выполнить следующие шаги:

2. С использованием формулы процента. Формула процента позволяет найти процент относительно другого значения по следующей формуле:

(Исходное значение * Процент) / 100 = Искомое значение

3. С помощью процентного коэффициента. Процентный коэффициент - это число, которое при умножении на исходное значение дает искомое значение. Для расчета процентного коэффициента необходимо выполнить следующие шаги:

Процентный коэффициент = Процент / 100

4. С использованием процентного отношения. Процентное отношение показывает, во сколько раз искомое значение больше или меньше исходного значения. Для расчета процентного отношения нужно выполнить следующие шаги:

Процентное отношение = Искомое значение / Исходное значение * 100

5. С помощью таблицы умножения. Таблица умножения позволяет найти искомое значение, умножая исходное значение на процент, выраженный десятичной дробью.

Выберите один из этих способов расчета в зависимости от вашей задачи и используйте его для нахождения процента относительно другого значения. Не забывайте проверять свои вычисления, чтобы быть уверенным в правильности результата. Удачи в расчетах!

Третий способ расчета процента относительно другого значения

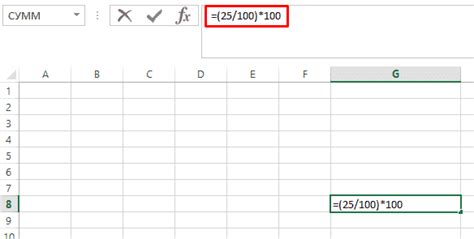
Третий способ расчета процента относительно другого значения основан на использовании простого правила трех. Этот метод особенно полезен при нахождении процента увеличения или уменьшения от исходного значения.

Чтобы найти процент относительно другого значения, нужно сначала определить разницу между исходным и новым значением, а затем найти процент этой разницы от исходного значения.

Пусть у нас есть исходное значение X и новое значение Y. Тогда разница между ними будет равна Y - X. Чтобы найти процент этой разницы от исходного значения, нужно выразить разницу в процентах от X с помощью следующего выражения:

Процент = (разница / X) * 100

После расчета этого выражения получим процент отношения нового значения к исходному значению.

Например, если исходное значение равно 100, а новое значение равно 120, то разница между ними составит 120 - 100 = 20. Для нахождения процента этой разницы относительно исходного значения нужно выполнить следующие расчеты:

Процент = (20 / 100) * 100 = 20%

Таким образом, процент отношения нового значения 120 к исходному значению 100 составляет 20%.

Четвертый способ расчета процента относительно другого значения

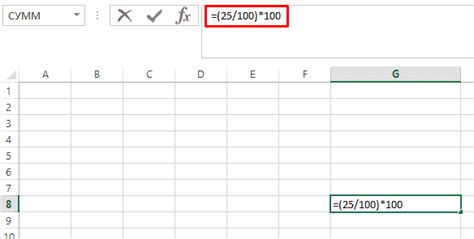
Найдение процента относительно другого значения можно осуществить с помощью простого математического расчета. Для этого необходимо знать два числа: исходное значение и процентное отношение, которое нужно найти.

Для начала необходимо разделить исходное значение на 100, чтобы получить один процент. Затем этот результат умножается на процентное отношение, которое нужно найти. Полученное число будет искомым значением процента относительно исходного значения.

Например, если у нас есть число 300 и мы хотим найти 20% от этого числа, то нужно выполнить следующие шаги:

1. Разделить 300 на 100: 300 / 100 = 3
2. Умножить результат на 20: 3 * 20 = 60

Итак, 20% от числа 300 равно 60.

Этот метод можно использовать для нахождения процентов относительно любого значения. Для этого достаточно знать исходное значение и процентное отношение, которое нужно найти. Помните, что результат всегда будет выражен в процентах от исходного значения.