Простые числа - это особая категория целых чисел, которые могут быть делены только на себя и на единицу без остатка. Они являются фундаментальными элементами арифметики и имеют важное значение в различных областях науки и технологий.
Получение простых чисел является актуальной задачей, особенно в современной вычислительной математике. Множество алгоритмов и методов позволяют находить простые числа, но одной из самых эффективных и быстрых процедур является метод решета Эратосфена.
Метод решета Эратосфена основывается на простом алгоритме: сначала выписываются все числа от 2 до заданного предела, а затем последовательно вычеркиваются числа, являющиеся кратными предыдущим числам. Таким образом, остаются только простые числа.
Применение метода решета Эратосфена позволяет получать простые числа за минимальное время и с высокой точностью. Этот метод широко применяется в различных областях, таких как криптография, компьютерные сети и математическое моделирование.
Получение простого целого числа

Метод перебора заключается в проверке каждого числа от 2 до n на делимость на остальные числа. Если число не делится ни на одно из предыдущих чисел, то оно считается простым.
Однако этот метод является неэффективным для больших чисел, так как требует большого количества операций. Для получения простых чисел быстрее можно использовать различные алгоритмы, такие как решето Эратосфена или тест Миллера-Рабина.
Решето Эратосфена позволяет найти все простые числа до заданного числа n. Оно основано на принципе исключения: изначально все числа от 2 до n считаются простыми, затем перебираются все числа от 2 до n и помечаются как составные, если они делятся на другое простое число. В конце остаются только простые числа.
Тест Миллера-Рабина является вероятностным алгоритмом проверки числа на простоту. Он основан на теореме Ферма и использует случайные числа и операции возведения в степень для проверки простоты числа. Однако этот метод не гарантирует абсолютной точности и может давать ложные положительные или ложные отрицательные результаты.
Выбор метода для получения простого числа зависит от задачи, с которой вы работаете. Если вам необходимо получить все простые числа до определенного числа, то решето Эратосфена может быть наиболее эффективным. Если же вам нужно простое число для проверки простоты других чисел, то тест Миллера-Рабина может быть подходящим выбором.
Зачем нужны простые числа?

| Шифрование и безопасность | Простые числа играют важную роль в криптографии и безопасности сетей. На основе простых чисел строятся мощные шифры и криптографические алгоритмы, которые обеспечивают безопасность передачи данных. |
| Делители и разложение на множители | Простые числа сохраняют свою уникальность в разложении других чисел. Любое натуральное число можно представить в виде произведения простых чисел. Это свойство простых чисел помогает в решении различных задач, связанных с делителями и разложением чисел. |
| Математические теории | Простые числа являются объектом исследований в различных математических теориях. Изучение и свойства простых чисел позволяют установить закономерности и общие правила, которые затрагивают широкий спектр математических исследований. |
| Оптимизация и эффективность | Простые числа используются для оптимизации и повышения эффективности различных алгоритмов и вычислительных задач. Использование простых чисел позволяет сократить время выполнения некоторых операций и упростить сложные вычисления. |
Итак, простые числа играют важную роль в различных областях, от криптографии и безопасности до математических исследований и оптимизации алгоритмов. Понимание и использование простых чисел имеет практическое и теоретическое значение и является неотъемлемой частью современной науки и техники.
Определение простого числа

Определение простого числа можно представить в виде таблицы, где первый столбец содержит числа, а второй столбец показывает, является ли число простым или нет.
| Число | Простое |
|---|---|
| 2 | Да |
| 3 | Да |
| 4 | Нет |
| 5 | Да |
| 6 | Нет |
| 7 | Да |
| 8 | Нет |
| 9 | Нет |
| 10 | Нет |
Таким образом, числа 2, 3, 5 и 7 являются простыми числами, в то время как числа 4, 6, 8, 9 и 10 не являются простыми.
Методы получения простых чисел

Метод перебора
Простейший способ получить простые числа - это метод перебора. Он заключается в последовательной проверке всех целых чисел больше 1 на делимость на другие числа. Начиная с числа 2, каждое число проверяется на возможность деления на все числа от 2 до n-1, где n - число, которое мы проверяем. Если число n не делится ни на одно из проверяемых чисел, то оно является простым.
Метод решета Эратосфена
Более эффективным методом получения простых чисел является решето Эратосфена. Оно основано на принципе исключения. Сначала создается список всех чисел от 2 до заданного верхнего предела. Затем начинается процесс исключения: сначала из списка удаляются все числа, кратные 2, затем все числа, кратные 3 и т.д. Таким образом, в конечном итоге останутся только простые числа.
Метод теста простоты Миллера-Рабина
Существуют также более сложные алгоритмы нахождения простых чисел, например, тест простоты Миллера-Рабина. Он основан на алгоритме теста Ферма и используется для проверки числа на простоту. Он не гарантирует абсолютно точный результат, но обычно дает достаточно хорошую оценку и используется в криптографии и других областях, где требуется быстрая генерация простых чисел.
Перебор делителей
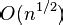
Если в результате перебора делителей не найден ни один делитель, то число является простым.
Перебор делителей работает на принципе исключения. Если мы не находим делитель в диапазоне от 2 до корня из числа, значит, его делители должны быть больше корня из числа. Это позволяет сократить количество операций и ускорить время получения простого числа.
Такой метод подходит для получения небольших простых чисел, но для более больших чисел может быть неэффективным. В таких случаях рекомендуется использовать более сложные алгоритмы, такие как алгоритмы решета Эратосфена или тест Миллера-Рабина.
Однако, перебор делителей позволяет достаточно быстро получить простые числа в небольшом диапазоне и является простым в реализации.
Решето Эратосфена

Шаги алгоритма:
- Создать массив чисел от 2 до N.
- Начиная с числа 2, отметить все его кратные числа в массиве.
- Перейти к следующему неотмеченному числу.
- Повторять шаги 2 и 3, пока не будут отмечены все числа до N.
После выполнения алгоритма в массиве останутся только простые числа. Это происходит потому, что каждый раз, когда мы отмечаем кратное число, мы на самом деле обнаруживаем, что оно не простое.
Решето Эратосфена позволяет получить простые числа в заданном диапазоне за минимальное время. Оно особенно полезно, когда требуется найти все простые числа до большого числа.
Метод Ферма
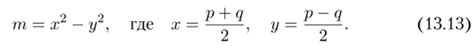
Один из самых быстрых способов получения простых чисел – метод Ферма. Метод Ферма основан на простой идее: если число n простое, то для каждого целого a справедливо равенство a^n-1 = 1 (mod n).
Процесс получения простого числа по методу Ферма включает следующие шаги:
- Выбрать случайное число a из интервала (2, n-1).
- Вычислить a^n-1 mod n.
- Если полученный результат не равен 1, то число n составное, и нужно выбрать новое значение a.
- Если полученный результат равен 1, повторить шаги 1-3 с новым значением a.
- Повторять процесс до достижения требуемой точности или получения простого числа.
Метод Ферма обладает высокой скоростью работы и хорошей вероятностью получения простого числа, но не гарантирует, что все полученные числа будут действительно простыми. Для повышения точности и надежности результата рекомендуется применять другие алгоритмы и фильтры, такие как тест Миллера-Рабина или решето Эратосфена.
Как быстро получить простые числа
- Метод решета Эратосфена
- Тест Миллера-Рабина
- Формула Вильсона
- Рандомизированные алгоритмы
Один из самых известных и простых способов получения простых чисел – это метод решета Эратосфена. Этот метод основывается на принципе исключения. Сначала создается список всех чисел от 2 до заданного верхнего предела. Затем последовательно вычеркиваются все числа, которые являются кратными какому-либо числу в списке. Оставшиеся числа будут простыми.
Другой популярный метод получения простых чисел – это тест Миллера-Рабина. Этот метод основывается на проверке числа на простоту с использованием модулярного возведения в степень. Если число не проходит тест, то оно точно не является простым. Если число проходит несколько итераций теста, то вероятность его простоты становится очень высокой.
Формула Вильсона – это математическое утверждение, которое позволяет определить простое число. Если число p является простым, то (p-1)! + 1 без остатка делится на p. Однако данная формула не является эффективным методом получения простых чисел, потому что для больших чисел вычисление факториала становится очень затратным.
Существует также класс рандомизированных алгоритмов, которые используют случайные числа для определения простоты числа. Рандомизированные алгоритмы основываются на вероятностной проверке числа на простоту и могут быть эффективными для больших чисел.
Выбор конкретного метода получения простых чисел зависит от задачи и требуемой эффективности. Описанные выше методы представляют лишь некоторые из подходов к получению простых чисел и позволяют выбрать наиболее подходящий вариант в конкретной ситуации.
Оптимизация перебора делителей

Существуют различные методы оптимизации перебора делителей:
- Остановка после нахождения первого делителя: после нахождения первого делителя число уже не может быть простым, поэтому перебор может быть прекращен.
- Пропуск четных чисел: поскольку все четные числа, кроме двойки, не являются простыми, их можно сразу исключить из перебора.
- Использование уже найденных простых чисел: когда уже найдены простые числа меньше текущего числа, можно использовать их для проверки делимости.
- Использование решета Эратосфена: данный метод позволяет найти все простые числа в заданном диапазоне до предела, используя меньшее количество операций.
Использование этих методов позволяет существенно ускорить поиск простых чисел и сделать его более эффективным.