Длина дуги является одним из важных понятий в геометрии, особенно при работе с окружностями. Она представляет собой отрезок, который составляет часть окружности между двумя указанными концами. Если вам необходимо найти длину дуги в градусах, то вам понадобится знание некоторых основных принципов и формул.
Во время изучения геометрии вы наверняка сталкивались с градусной мерой угла. Градус - это единица измерения, которая используется для указания размера угла. Одна полная окружность состоит из 360 градусов. Таким образом, дуга, составляющая половину окружности, будет состоять из 180 градусов.
Для вычисления длины дуги в градусах вам понадобится знание длины окружности и размера угла в градусах. Формула для расчета длины дуги выглядит следующим образом:
L = (C/360) * α
Где L - длина дуги, C - длина окружности, α - размер угла в градусах. Итак, если у вас есть значения длины окружности и размера угла, подставьте их в формулу и произведите расчет.
Как найти длину дуги в градусах
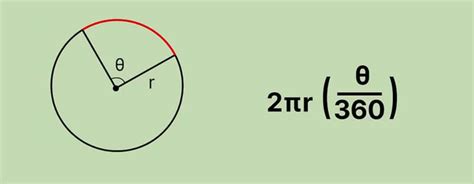
Длина дуги в градусах вычисляется с использованием формулы, которая основана на измерении углов в градусах. Для нахождения длины дуги требуется знание радиуса окружности и величины центрального угла, в градусах, описываемого этой дугой.
Формула для вычисления длины дуги в градусах имеет вид:
L = (𝜋 * d * 𝛼) / 180
Где:
- L - длина дуги в градусах
- 𝜋 - математическая константа, примерное значение которой равно 3.14159
- d - диаметр окружности, если известен, или радиус окружности в случае его использования
- 𝛼 - величина центрального угла, измеряемая в градусах
Применение этой формулы позволяет легко находить длину дуги в градусах при использовании известных значений радиуса окружности и центрального угла. Для правильного нахождения длины дуги необходимо обратить внимание на единицы измерения, а также использовать корректные значения для всех переменных в формуле.
Что такое длина дуги
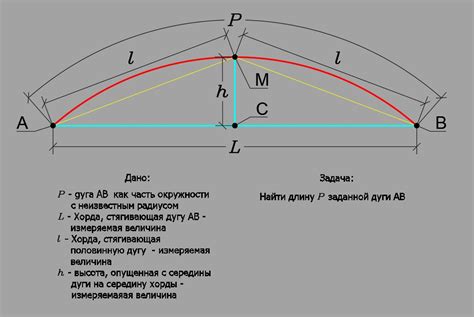
Длина дуги в градусах представляет собой меру распределения точек на окружности. Она измеряется в градусах и определяется как часть окружности, ограниченная двумя указанными углами.
Для вычисления длины дуги необходимо знать радиус окружности и центральный угол, который составляет дуга. Формула расчета длины дуги выглядит следующим образом:
| Длина дуги | = | 2π * Радиус * (Центральный угол / 360°) |
В этой формуле 2π представляет собой число Пи (π), округленное до нужного количества знаков после запятой. Радиус и центральный угол измеряются в градусах.
Зная радиус окружности и центральный угол, можно вычислить длину дуги, что позволяет определить протяженность и положение объекта на окружности.
Какой принцип измерения длины дуги
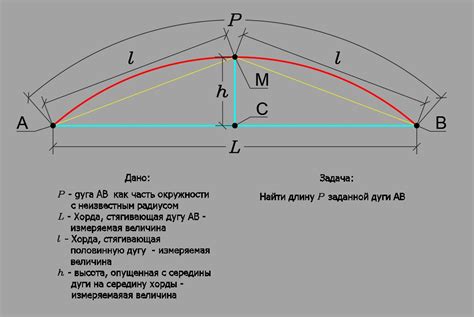
Измерение длины дуги происходит с помощью угла, образованного этой дугой и центральным углом. Длина дуги измеряется в градусах, а формула для расчета длины дуги зависит от радиуса окружности и величины центрального угла.
Формула для расчета длины дуги выглядит следующим образом:
L = r * (pi/180) * α
Где:
- L - длина дуги;
- r - радиус окружности, на которой находится дуга;
- pi - математическая константа, приближенное значение которой равно 3.14159;
- α - центральный угол, измеряемый в градусах.
Для расчета длины дуги необходимо знать значение радиуса и центрального угла. Подставив эти значения в формулу, можно определить длину дуги в градусах.
Например, если радиус окружности равен 8 см, а центральный угол равен 45 градусов, то длина дуги будет:
L = 8 * (pi/180) * 45
После выполнения вычислений можно получить конкретное значение длины дуги в градусах.
Как рассчитать длину дуги в градусах
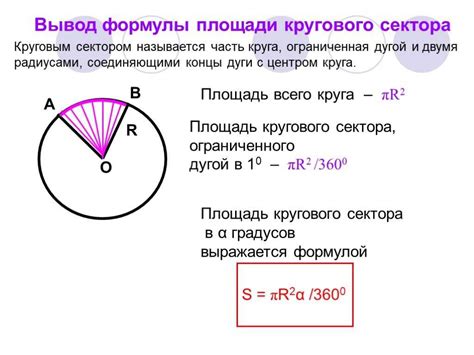
Для начала, необходимо знать длину окружности, на которой находится дуга. Формула для расчета длины окружности выглядит следующим образом:
L = 2πr
Где L – длина окружности, π – математическая константа, примерное значение которой равно 3.14 (но для более точных расчетов можно использовать большее количество знаков после запятой), r – радиус окружности.
Зная длину окружности, можно найти длину дуги в градусах с помощью пропорции. Все окружность разделена на 360 градусов, следовательно, длина дуги в градусах равна:
Длина_дуги_в_градусах = (градусы / 360) * Длина_окружности
Теперь, подставив в формулу известные значения, можно получить результат – длину дуги в градусах.
Например, пусть радиус окружности равен 5 единиц, а угол, определяющий дугу, составляет 60 градусов. Приблизительное значение константы π возьмем равным 3.14.
L = 2 * 3.14 * 5 = 31.4
Длина_дуги_в_градусах = (60 / 360) * 31.4 = 5.23
Таким образом, длина дуги, ограниченной углом 60 градусов на окружности с радиусом 5 единиц, составляет примерно 5.23 единицы.
Эта формула может быть полезна в различных ситуациях, связанных с геометрией и физикой, например, при расчете траектории движения объекта по окружности или при определении угла поворота для навигации.
Формула для расчета длины дуги в градусах
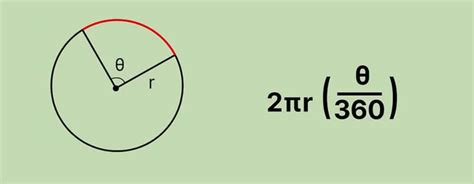
Длина дуги представляет собой часть окружности, которая измеряется в градусах. Чтобы рассчитать длину дуги в градусах, необходимо знать радиус окружности и центральный угол, в градусах, который она охватывает. Для этого применяется следующая формула:
Л = (2π * R * α) / 360,
где:
- Л - длина дуги в градусах;
- R - радиус окружности;
- α - центральный угол, в градусах, который охватывает окружность.
Применяя эту формулу, можно легко рассчитать длину дуги в градусах, если известны значения радиуса и центрального угла. Этот расчет может быть полезен при работе с геометрическими фигурами или в задачах, связанных с измерениями и построениями.
Пример расчета длины дуги в градусах
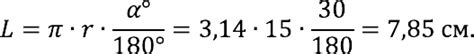
Для начала рассчитаем длину всей окружности с помощью формулы:
C = 2πR
где C - длина окружности, π - математическая константа, примерно равная 3.14159, и R - радиус окружности.
Теперь рассчитаем, какую часть от всей окружности составляет наш угол. Это можно сделать с помощью формулы:
L = (α/360) * C
где L - длина дуги в градусах, α - измеряемый угол в градусах, а С - длина всей окружности.
Например, предположим, что у нас есть окружность с радиусом 5 см, а мы хотим найти длину дуги для угла в 45 градусов.
Сначала рассчитаем длину всей окружности:
C = 2 * 3.14159 * 5 = 31.4159 см
Теперь рассчитаем длину дуги для угла в 45 градусов:
L = (45/360) * 31.4159 = 3.92699 см
Таким образом, длина дуги окружности для угла в 45 градусов равна примерно 3.927 см.
Важные факторы, влияющие на длину дуги
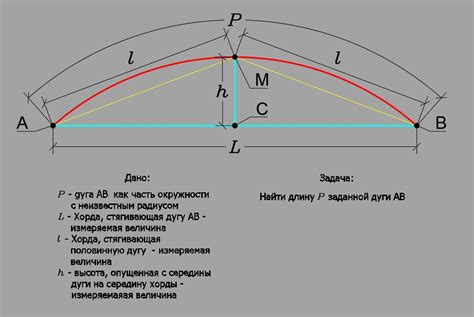
Важные факторы, которые влияют на длину дуги, включают:
- Радиус окружности или эллипса: Длина дуги прямо пропорциональна радиусу. Чем больше радиус, тем больше будет длина дуги и наоборот.
- Центральный угол: Длина дуги также зависит от величины центрального угла между точками. Чем больше угол, тем больше будет длина дуги.
- Единицы измерения: Длина дуги может быть измерена в различных единицах: радианы, градусы или радиусные доли. При переходе от одних единиц измерения к другим длина дуги также может изменяться.
Обратите внимание, что при расчете длины дуги необходимо учитывать все эти факторы вместе. Формулы для расчета длины дуги могут включать учет радиуса, центрального угла и единиц измерения.
Практические применения расчета длины дуги в градусах
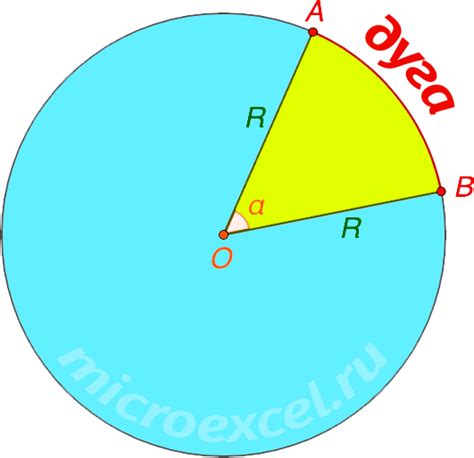
- Геодезия: Расчет длины градусной дуги на земной поверхности позволяет определить расстояние между двумя точками на поверхности Земли. Это особенно полезно при измерении географических координат и определении расстояний на межконтинентальных маршрутах.
- Картирование: В картировании, особенно при построении карт местности или трехмерных моделей, измерение длины дуги в градусах помогает определить масштаб карты и правильно показать пространственные отношения между объектами.
- Астрономия: В астрономии расчет длины дуги в градусах необходим для определения координат и движения небесных тел. Это помогает астрономам определить положение и траекторию планеты, звезды, спутника и других небесных объектов на небесной сфере.
- Инженерное дело: В инженерном деле, особенно в строительстве, измерение длины дуги в градусах используется для определения угловых отклонений, поворотных углов и кривых радиуса на строительных площадках и в различных инженерных конструкциях.
- Навигация: Расчет длины дуги в градусах является ключевым элементом в навигации на суше, море и в воздухе. Он позволяет определить направление, расстояние и время между точками назначения. Например, пилоты используют этот расчет для трассировки и навигации своих воздушных судов.
Это лишь некоторые из практических применений расчета длины дуги в градусах. Все они демонстрируют важность этого инструмента в различных областях и практическую необходимость его применения.