Функция Лапласа – это математическая функция, часто используемая в теории вероятностей и статистике. Она позволяет вычислить вероятность того, что случайная величина будет равна или меньше заданного значения. Функция Лапласа широко применяется в различных областях, таких как экономика, инженерия и физика.
Основная идея функции Лапласа заключается в преобразовании исходной случайной величины в стандартную нормальную случайную величину, чья функция распределения известна. Затем используется таблица значений функции Лапласа или специальные программы для вычисления значения искомой вероятности.
Рассмотрим пример, чтобы лучше понять, как использовать функцию Лапласа. Предположим, что мы имеем набор данных о стоимости товара в магазине и хотим узнать, какая вероятность того, что случайно выбранный товар будет стоить не более определенной суммы. Мы можем использовать функцию Лапласа, чтобы вычислить эту вероятность.
Сначала нужно нормализовать исходные данные, то есть привести их к стандартному нормальному распределению с математическим ожиданием равным нулю и стандартным отклонением равным единице. Затем находим значение функции Лапласа для заданной суммы и используем таблицу значений, чтобы найти соответствующую вероятность.
Методы нахождения значения функции Лапласа
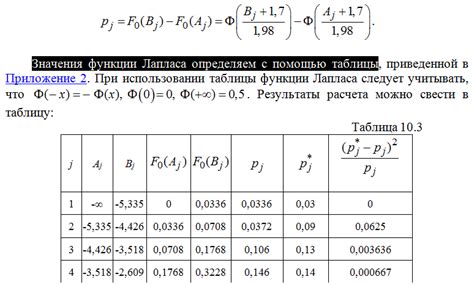
Существует несколько методов для нахождения значения функции Лапласа:
| Метод | Описание |
|---|---|
| Таблицы значений | Самым простым способом нахождения значений функции Лапласа является использование таблиц, которые содержат значения функции для различных комбинаций аргументов. Эти таблицы могут быть найдены в статистических справочниках или книгах по математике. |
| Аппроксимация | В случаях, когда нет готовых таблиц значений функции Лапласа, можно использовать методы аппроксимации. Это подразумевает использование математических формул или алгоритмов для приближенного нахождения значений функции. |
| Вычисление с использованием программного обеспечения | Современные компьютерные программы и пакеты, такие как Microsoft Excel или MATLAB, имеют функции, которые позволяют вычислять значения функции Лапласа. Это более точный и удобный способ, особенно при работе с большими наборами данных. |
Выбор метода нахождения значения функции Лапласа зависит от доступных ресурсов и требуемой точности. Во многих случаях таблицы значений или аппроксимация являются достаточно точными и удобными способами, но при высоких требованиях к точности и работе с большими объемами данных лучше использовать программное обеспечение.
Руководство по использованию таблицы значений
Чтобы воспользоваться таблицей значений, необходимо знать значение аргумента и искомую вероятность. Найдите нужное значение аргумента в одной из колонок таблицы и соответствующую вероятность находите в строке, расположенной ниже. Точное значение функции Лапласа указывается в пересечении найденной вертикальной и горизонтальной ячеек.
В таблице значений функции Лапласа могут быть представлены значения аргумента от -3 до 3 и вероятности от 0,00 до 0,50. Если нужное вам значение находится вне этого диапазона, воспользуйтесь интерполяцией для определения значения функции Лапласа.
При использовании таблицы необходимо обратить внимание на аргумент функции Лапласа и вероятность, для которой мы ищем значение. Аргумент может быть выражен как положительное, так и отрицательное число, соответствующее правильному знаку находится в таблице. Вероятность обычно указывается до сотых или тысячных долей, поэтому внимательно следите за точностью своих вычислений.
Например, чтобы найти значение функции Лапласа для аргумента x = 1,2 и вероятности p = 0,8, найдите значение 1,2 в столбце аргументов и значение 0,8 в строке вероятностей. В пересечении найденной ячейки будет указано искомое значение функции Лапласа.
Использование таблицы значений функции Лапласа является удобным способом быстро получить значения функции без необходимости проведения сложных математических вычислений. Зная основные принципы работы с таблицей, вы сможете успешно решать задачи из области вероятностей и статистики.
Примеры решения задач с использованием функции Лапласа

Пример 1:
Пусть случайная величина X имеет нормальное распределение с средним значением µ = 0 и стандартным отклонением σ = 1. Найти вероятность P(X ≤ 2).
Решение:
Для решения этой задачи можно использовать таблицу значений функции Лапласа. В таблице нужно найти значение для z-статистики, которая равна (2 - µ) / σ.
В данном случае z-статистика равна (2 - 0) / 1 = 2. По таблице значений функции Лапласа для z = 2 можно найти вероятность P(Z ≤ 2), которая составляет примерно 0.9772. Таким образом, вероятность P(X ≤ 2) также составляет примерно 0.9772.
Пример 2:
Пусть случайная величина Y имеет экспоненциальное распределение с параметром λ = 2. Найти вероятность P(Y ≤ 4).
Решение:
Для решения этой задачи можно использовать функцию Лапласа следующим образом:
P(Y ≤ 4) = 1 - exp(-λt), где t - значение, для которого нужно найти вероятность.
Подставим значения в формулу: P(Y ≤ 4) = 1 - exp(-2 * 4) ≈ 1 - exp(-8) ≈ 1 - 0.0003 ≈ 0.9997.
Таким образом, вероятность P(Y ≤ 4) составляет примерно 0.9997.
Пример 3:
Пусть случайная величина Z имеет стандартное нормальное распределение. Найти вероятность P(-1 ≤ Z ≤ 1).
Решение:
Для решения этой задачи нужно вычислить разность вероятностей P(Z ≤ 1) - P(Z ≤ -1).
Используя таблицу значений функции Лапласа, находим, что P(Z ≤ 1) ≈ 0.8413 и P(Z ≤ -1) ≈ 0.1587. Следовательно, P(-1 ≤ Z ≤ 1) ≈ 0.8413 - 0.1587 ≈ 0.6826.
Таким образом, вероятность P(-1 ≤ Z ≤ 1) составляет примерно 0.6826.
Все эти примеры показывают, как использовать функцию Лапласа для нахождения вероятностей в различных моделях случайных процессов. Знание этой функции поможет в проведении анализа данных и принятии решений на основе статистических данных.