Косинус угла является одной из основных тригонометрических функций, широко применяемых в математике и физике. Процесс нахождения косинуса угла может быть неочевидным и запутанным для некоторых людей. Однако, с небольшими объяснениями и пошаговым подходом можно легко освоить это умение.
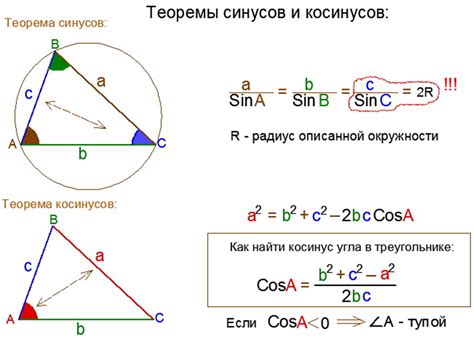
Прежде чем приступать к нахождению косинуса угла, необходимо понять, что такое косинус. Косинус угла abc - это отношение длины прилежащего катета к гипотенузе прямоугольного треугольника, где угол abc смежный углу прямого треугольника.
Чтобы найти косинус угла abc, необходимо выполнить несколько шагов. Во-первых, изучите прямоугольный треугольник, в котором находится данный угол. Во-вторых, определите длины катетов и гипотенузы этого треугольника. В-третьих, используя формулу для косинуса, расчитайте значение косинуса угла abc.
Что такое косинус угла?
Косинус угла обозначается как cos(α), где α - вершина угла, а cos - сокращенное название функции. Значение косинуса угла всегда лежит в диапазоне от -1 до 1, где -1 соответствует углу 180 градусов (или π радиан), а 1 соответствует углу 0 градусов (или 0 радиан).
Косинус угла можно вычислить с использованием тригонометрических таблиц или с помощью специальных функций на калькуляторе или компьютере. Также существуют формулы и алгоритмы для вычисления косинуса угла на основе известных значений сторон треугольника или прилежащего угла.
Косинус угла имеет множество приложений в математике, физике, инженерии и других науках. Например, в геометрии он используется для измерения расстояний и углов в пространстве, в физике - для описания колебаний и волн, а в компьютерной графике - для создания трехмерных моделей и эффектов.
Шаг 1: Понятия и термины

Прежде чем мы начнем вычислять косинус угла ABC, давайте разберемся с основными понятиями и терминами, связанными с этой задачей:
- Угол ABC: это угол, образованный лучами AB и BC.
- Косинус угла ABC: это отношение длины стороны BC к гипотенузе треугольника ABC.
- Гипотенуза треугольника ABC: это самая длинная сторона треугольника, которая соединяет два несмежных угла (в данном случае, сторона AC).
- Сторона BC: это одна из сторон треугольника ABC, противолежащая углу ABC.
Теперь, когда мы понимаем эти основные термины, мы готовы перейти к следующему шагу - вычислению косинуса угла ABC.
Угол abc и его особенности
Особенности угла abc включают следующие:
| Тип угла | Описание |
| Острый угол | Если угол abc меньше 90 градусов. |
| Прямой угол | Если угол abc равен 90 градусов. В этом случае лучи ab и bc являются перпендикулярными. |
| Тупой угол | Если угол abc больше 90 градусов, но меньше 180 градусов. В этом случае один из лучей, ab или bc, лежит внутри другого луча. |
| Развернутый угол | Если угол abc равен 180 градусов. В этом случае лучи ab и bc представляют собой продолжение друг друга. |
| Смежные углы | Если угол abc имеет общую сторону с другим углом и точку b, являющуюся конечной точкой луча ab, является начальной точкой другого луча. |
| Вертикально противоположные углы | Если угол abc имеет общую сторону с другим углом и точки a и c являются точками пересечения лучей ab и cd соответственно. |
Понимание особенностей угла abc позволяет более точно определять его значение и использовать тригонометрические функции для нахождения значения косинуса угла abc.
Шаг 2: Формула косинуса

Косинус угла ABC можно найти с помощью формулы косинуса, которая выражается следующим образом:
cos(ABC) = (AB^2 + BC^2 - AC^2) / (2 * AB * BC)
Где:
- AB - длина стороны AB
- BC - длина стороны BC
- AC - длина стороны AC
Для вычисления косинуса угла ABC, необходимо знать длины всех трех сторон треугольника ABC. Зная эти значения, мы можем подставить их в формулу косинуса и вычислить значение косинуса угла ABC.
Как использовать формулу косинуса для нахождения угла abc
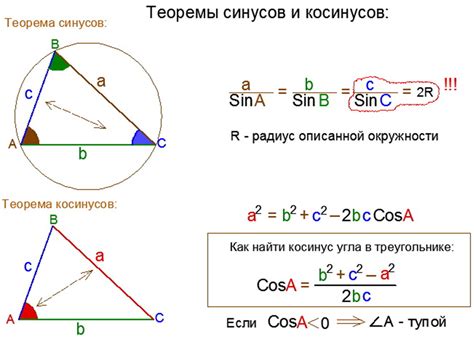
Для нахождения косинуса угла ABC пошагово можно использовать формулу косинуса и известные значения сторон треугольника ABC. Формула косинуса гласит:
cos(ABC) = (b^2 + c^2 - a^2) / 2bc
Где:
- ABC - угол, косинус которого мы хотим найти.
- a, b, c - длины сторон треугольника ABC. Сторона a противолежит углу ABC, сторона b - углу BCA, сторона c - углу CAB.
Для нахождения косинуса угла ABC пошагово, необходимо:
- Определить значения длин сторон треугольника ABC.
- Возвести значения сторон в квадрат и вычислить их сумму.
- Вычислить разность суммы квадратов сторон и квадрата стороны, противолежащей углу ABC.
- Поделить полученное значение на произведение длин сторон, проходящих через угол ABC.
- Полученное значение будет являться косинусом угла ABC.
Применение указанных шагов позволит вам пошагово использовать формулу косинуса для нахождения угла ABC.
Шаг 3: Определение значений sin и cos

Для определения значения косинуса угла abc, необходимо сначала вычислить значения синуса и косинуса для каждого из углов a, b и c. Затем используя полученные значения, можно найти значение косинуса угла abc.
Для определения синуса и косинуса угла a, можно воспользоваться таблицей значений тригонометрических функций или различными онлайн-калькуляторами.
Допустим, что значение синуса угла a равно 0.5, а значение косинуса равно 0.866. Аналогично, для угла b значение синуса равно 0.866, а косинуса - 0.5.
Теперь все значения синуса и косинуса известны:
| Угол | Синус | Косинус |
|---|---|---|
| a | 0.5 | 0.866 |
| b | 0.866 | 0.5 |
| c | ? | ? |
Теперь, чтобы найти значение косинуса угла abc, можно воспользоваться формулой:
cos(abc) = cos(a + b + c) = cos(a) * cos(b) - sin(a) * sin(b)
Подставим значения, которые мы уже знаем:
cos(abc) = (0.866 * 0.5) - (0.5 * 0.866)
cos(abc) = 0.433 - 0.433
cos(abc) = 0
Таким образом, значение косинуса угла abc равно 0.
Как определить значения sin и cos угла abc
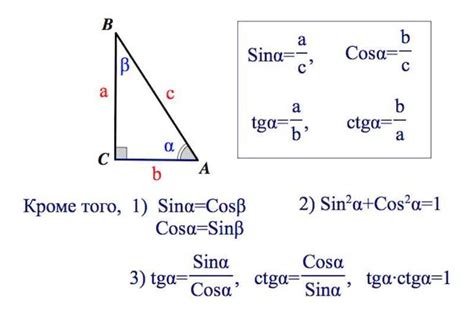
Чтобы определить значения sin и cos угла abc, необходимо руководствоваться следующими шагами:
- Найдите длины сторон треугольника abc. Для этого можно использовать известную длину двух сторон и известный угол, либо применить теорему Пифагора для нахождения третьей стороны.
- Определите, какой из трех углов треугольника является углом abc. Обычно этот угол обозначают буквой c.
- Для определения значения sin и cos угла c воспользуйтесь таблицей значений синуса и косинуса для различных углов. Подставьте значение угла c в таблицу и найдите соответствующие значения sin и cos.
- Запишите полученные значения sin и cos для угла abc.
Теперь вы знаете, как определить значения sin и cos угла abc. Эти значения могут быть полезны при решении задач из различных областей, таких как геометрия, физика и технические науки.
Шаг 4: Пошаговое руководство

Чтобы найти косинус угла abc, выполните следующие действия:
Шаг 1: Определите значения сторон a, b и c треугольника abc.
Шаг 2: Воспользуйтесь формулой косинуса:
cos(abc) = (a^2 + b^2 - c^2) / (2 * a * b)
Шаг 3: Подставьте известные значения сторон в формулу.
Шаг 4: Вычислите косинус угла abc, выполнив необходимые арифметические операции.
Таким образом, вы найдете косинус угла abc и сможете использовать его согласно вашим потребностям.
Как найти косинус угла abc пошагово
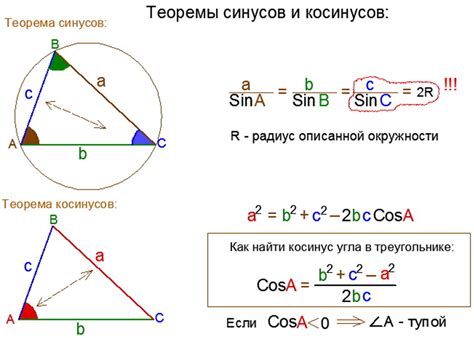
Косинус угла abc может быть найден с помощью следующих шагов:
Шаг 1: Определите значения сторон треугольника abc. Убедитесь, что у вас есть достаточно информации для решения задачи.
Шаг 2: Используйте формулу косинуса треугольника для вычисления косинуса угла abc. Формула выглядит следующим образом:
cos(abc) = (a^2 + b^2 - c^2) / (2 * a * b)
Где a, b, c - стороны треугольника abc.
Шаг 3: Подставьте известные значения сторон в формулу и выполните необходимые вычисления.
Шаг 4: Полученный результат будет являться значением косинуса угла abc.
Используя эти шаги, вы сможете найти косинус угла abc. Убедитесь, что ваш калькулятор настроен на градусы или радианы в зависимости от ваших потребностей.