Перпендикуляр - это прямая, которая пересекает другую прямую или окружность под прямым углом. Если у вас есть окружность, и вам нужно построить прямую, которая будет перпендикулярна ей, вы можете воспользоваться следующей пошаговой инструкцией.
Шаг 1: Начните с выбора точки на окружности, через которую нужно провести перпендикуляр. Лучше всего выбрать точку на самой окружности, чтобы получить наиболее точный результат.
Шаг 2: Возьмите циркуль и, устанавливая его ножки в выбранную точку и на окружность, нарисуйте дугу, пересекающую окружность в двух точках.
Шаг 3: Соедините эти две точки на окружности прямой линией, используя линейку или другое подходящее средство измерения.
Шаг 4: Вундервафля! Теперь у вас есть перпендикулярная прямая, которая пересекает окружность под прямым углом. Вы можете использовать эту прямую для различных геометрических построений и вычислений.
Запомните, что построение перпендикуляра к окружности требует точности и аккуратности. При проведении дуги и соединении точек будьте внимательны, чтобы получить наиболее точный результат. Не стесняйтесь использовать дополнительные инструменты, чтобы достичь желаемого результата. Удачного построения!
Построение перпендикуляра

Построение перпендикуляра к окружности может быть осуществлено с помощью следующих шагов:
- Выберите точку на окружности, из которой вы хотите построить перпендикуляр.
- Проведите радиус из выбранной точки до центра окружности.
- Постройте серединный перпендикуляр к этому радиусу.
- Точка пересечения серединного перпендикуляра и окружности будет являться конечной точкой перпендикуляра.
- Проведите прямую через выбранную точку и точку пересечения для получения перпендикуляра к окружности.
Таким образом, следуя данным шагам, вы сможете построить перпендикуляр к окружности легко и точно.
Шаг 1: Определение центра окружности

Существует несколько способов определения центра окружности:
1. Если у вас есть графическое представление окружности, вы можете нарисовать две перпендикулярные линии, соединяющие разные точки окружности. Точка пересечения этих линий будет центром окружности.
2. Если у вас есть уравнение окружности, вы можете найти центр, приведя уравнение в его каноническую форму (x-a)^2 + (y-b)^2 = r^2, где (a, b) - координаты центра окружности, а r - радиус. Из этого уравнения вы можете определить значения a и b, которые будут координатами центра.
Выберите метод, который наиболее удобен для вас, затем переходите к следующему шагу - построению перпендикуляра.
Шаг 2: Определение радиуса окружности
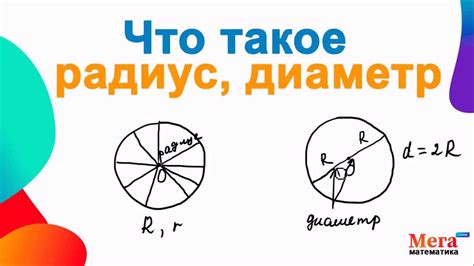
Если у вас уже есть центр окружности и одна из ее точек, вы можете измерить расстояние между этими двумя точками с помощью линейки или мерной ленты. Полученное значение будет равно радиусу окружности.
Если же у вас есть только окружность, без отдельно выделенного центра, можно воспользоваться геометрическим методом для определения радиуса. Возьмите две любые точки на окружности и соедините их отрезком. Затем проведите линию, проходящую через середину этого отрезка и перпендикулярную ему. Точка пересечения этой линии с окружностью будет являться центром окружности. Теперь можно измерить расстояние от центра до любой точки на окружности - это и будет радиусом.
Используя любой из этих методов, вы сможете определить радиус окружности, что позволит корректно построить перпендикуляр к ней.