Окружности и углы являются основными понятиями геометрии. Одним из интересных свойств окружностей является то, что вписанный угол (угол, вершина которого лежит на окружности, а стороны - на дугах окружности) и центральный угол (угол, вершина которого является центром окружности, а стороны - линии, соединяющие центр с точками на окружности) имеют особое взаимосвязанное положение.
Нахождение центрального угла из вписанного угла может быть важным для решения различных задач в геометрии и физике. Для этого требуется знание некоторых основных свойств окружностей и углов.
В данной статье рассмотрим алгоритм поиска центрального угла окружности из вписанного угла. Для начала необходимо понять, что вписанный угол всегда равен половине соответствующего центрального угла.
Формула для нахождения центрального угла:
Центральный угол = 2 * Вписанный угол.
Определение центрального угла окружности

Чтобы найти значение центрального угла, можно использовать следующую формулу:
- Разделить длину дуги, соответствующей центральному углу, на радиус окружности.
- Умножить полученное значение на 180°/π (пи).
Также можно найти значение центрального угла, используя связь между центральным углом и вписанным углом. Если вписанный угол и центральный угол имеют одну и ту же градусную меру, значит они равны.
Центральные углы являются важным понятием в геометрии и широко применяются в различных вычислениях и задачах.
Что такое центральный угол?

Вычисление центрального угла позволяет определить угол между двумя лучами, исходящими из центра окружности и проходящими через любую точку на окружности. Величина центрального угла измеряется в градусах или радианах и может быть разной, в зависимости от положения точек на окружности.
Центральные углы играют важную роль в различных областях математики и физики. Они используются для нахождения дуг окружности, расстояния между точками на окружности, а также для вычисления площадей и объемов тел.
Также центральные углы имеют важное значение в жизни: они помогают строить инженерные сооружения, определять географические координаты объектов и создавать красивые и гармоничные формы в архитектуре и дизайне.
Вписанный угол и связь с центральным углом
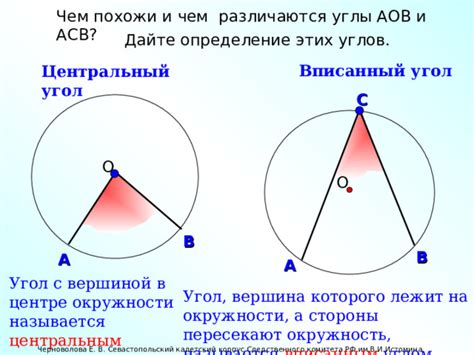
Для вписанного угла существует особая связь с центральным углом. Часто, чтобы найти центральный угол, соответствующий данному вписанному углу, можно воспользоваться простым правилом: центральный угол, дуга которого равна вписанному углу, будет вдвое больше данного вписанного угла.
Например, если вписанный угол равен 45 градусам, то соответствующий ему центральный угол будет равен 90 градусам.
Это свойство помогает упростить задачи по нахождению центрального угла, когда известен вписанный угол. Также, используя данную связь, можно решать задачи нахождения вписанных углов по данным о центральных углах.
Как найти центральный угол по вписанному углу

Если известно значение вписанного угла, то центральный угол можно найти, используя следующую формулу:
Центральный угол = 2 * вписанный угол
Например, если вписанный угол равен 30 градусов, то центральный угол будет равен:
Центральный угол = 2 * 30° = 60°
Таким образом, при знании величины вписанного угла можно легко и быстро найти значение центрального угла окружности.
Примеры решения задач на нахождение центрального угла

Для решения задач на нахождение центрального угла окружности из вписанного угла можно использовать следующий алгоритм:
1. Записать известные данные: вписанный угол и радиус окружности.
2. Установить соотношение между центральным и вписанным углом окружности:
центральный угол = 2 * вписанный угол
3. Подставить известные значения в формулу и рассчитать центральный угол.
Давайте рассмотрим несколько примеров решения задач на нахождение центрального угла:
Пример 1:
Дан вписанный угол окружности, равный 60 градусов. Радиус окружности равен 5 см. Найдем центральный угол.
Решение:
Центральный угол = 2 * 60 градусов = 120 градусов
Пример 2:
Дан вписанный угол окружности, равный 45 градусов. Радиус окружности равен 8 см. Найдем центральный угол.
Решение:
Центральный угол = 2 * 45 градусов = 90 градусов
Пример 3:
Дан вписанный угол окружности, равный 30 градусов. Радиус окружности равен 10 см. Найдем центральный угол.
Решение:
Центральный угол = 2 * 30 градусов = 60 градусов
Таким образом, зная значение вписанного угла и радиуса окружности, можно легко найти значение центрального угла. Эта информация может быть полезна для решения различных задач на геометрию и конструирование диаграмм.