Вопрос: Как построить квадрат, который полностью умещается внутри окружности, при этом обеспечивая высокую точность и эффективность выполнения? Ответ на этот вопрос может быть полезен тем, кто занимается геометрией, графикой, а также любителям математических головоломок.
Описание: Квадрат, вписанный в окружность, имеет ряд уникальных свойств и применений. Например, такой квадрат может быть использован для построения или расположения элементов дизайна, создания идеальных рамок для изображений или упаковки товаров. Но каким образом можно построить квадрат, который точно помещается внутри окружности без потери точности?
Решение: Существует несколько способов для построения точного и эффективного квадрата, который умещается внутри окружности. Один из них – использование известных формул и свойств геометрии. Для начала необходимо вычислить длину диагонали окружности, которая равна удвоенному радиусу. Затем, используя эту длину, можно получить длину стороны квадрата, применив соотношение, что длина диагонали квадрата равна квадратному корню из двух, умноженному на длину его стороны. Используя полученные значения радиуса и стороны квадрата, можно легко построить их на плоскости с высокой точностью и эффективностью.
Внимание: Необходимо учесть, что при построении квадрата вписанного в окружность, его углы будут совпадать с точками касания сторон квадрата и окружности. Это свойство может быть использовано для более точного и удобного построения данной геометрической фигуры.
Определение параметров окружности и квадрата
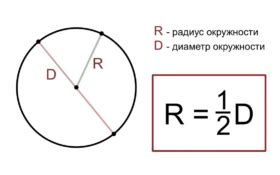
Окружность:
Окружность может быть определена при помощи радиуса или диаметра. Радиус окружности (R) – расстояние от центра окружности до любой точки на ее границе. Диаметр окружности (D) – двойной радиус, то есть расстояние между двумя точками на границе окружности, проходящими через ее центр.
Чтобы найти периметр окружности (P), используется формула: P = 2πR, где π (пи) – математическая константа, которая примерно равна 3,14159.
Площадь окружности (S) вычисляется по формуле: S = πR².
Квадрат:
Квадрат – это четырехугольник, все стороны которого равны между собой, а все углы прямые (равны 90 градусам).
Периметр квадрата (P) вычисляется по формуле: P = 4a, где а – длина стороны квадрата.
Площадь квадрата (S) вычисляется по формуле: S = a², где a – длина стороны квадрата.
Зная параметры окружности (радиус или диаметр), можно рассчитать параметры квадрата, вписанного в эту окружность, или наоборот, зная параметры квадрата, можно определить параметры окружности, его описывающей.
Нахождение радиуса окружности

Для построения квадрата вписанного в окружность необходимо знать радиус этой окружности. Радиус можно найти, используя различные методы.
Один из самых простых методов - это измерение диагонали квадрата и деление ее на два. Диагональ квадрата является диаметром окружности.
Другой метод - через измерение длины стороны квадрата и использование формулы, которая связывает радиус окружности и длину стороны квадрата:
Радиус = длина стороны квадрата / 2.
Также существует метод, основанный на измерении площади квадрата и использовании формулы, связывающей радиус окружности и площадь квадрата:
Радиус = sqrt(площадь квадрата) / 2.
Если известны координаты вершин квадрата или угол наклона его сторон, то радиус окружности можно найти с помощью геометрических формул.
| Метод | Применение |
|---|---|
| Измерение диагонали | Простой и быстрый метод для нахождения радиуса окружности. |
| Измерение стороны | Позволяет точно определить радиус окружности с помощью измерения длины стороны квадрата. |
| Измерение площади | Метод для определения радиуса окружности на основе площади квадрата. |
| Геометрические формулы | Позволяют найти радиус окружности на основе координат вершин квадрата или угла наклона его сторон. |
Выбор метода определяется доступностью измерительных инструментов и предпочтениями исследователя. Важно получить точные данные, чтобы построить эффективный и точный квадрат вписанный в окружность.
Вычисление длины стороны квадрата
Для построения эффективного и точного квадрата, который вписан в окружность, необходимо вычислить длину его стороны. Правильный вписанный в окружность квадрат имеет следующие свойства:
- Все стороны квадрата равны между собой.
- Диагональ квадрата является диаметром окружности.
Для вычисления длины стороны квадрата, можно использовать следующую формулу:
Сторона квадрата = Диаметр окружности / √2
Зная радиус или диаметр окружности, вы можете вычислить длину стороны квадрата с помощью этой формулы. Например, если радиус окружности равен 5 сантиметров, то длина стороны квадрата будет:
Сторона квадрата = 2 * Радиус * √2 = 2 * 5 * √2 = 10√2 сантиметров
Таким образом, длина стороны квадрата в данном случае будет равна примерно 14,1 сантиметра (округлено до одной десятой).
Вычисление длины стороны квадрата является важным шагом для построения и расчета параметров вписанного квадрата, и эта формула поможет вам достичь точных результатов.
Построение квадрата вписанного в окружность
Для начала, необходимо определить диаметр окружности. Пусть d будет диаметром окружности.
Затем, используя диаметр d, можно определить сторону квадрата. Сторона квадрата будет равна d.
Для построения квадрата вписанного в окружность, следует выполнить следующие шаги:
- Нарисовать окружность с центром O и радиусом R.
- Найти середину стороны окружности и отметить точку A.
- Соединить точки O и A прямой линией.
- Провести прямую линию, перпендикулярную прямой OA, через середину стороны окружности.
- Найти точки B и C, где эта прямая пересекает окружность. Точки B и C являются вершинами квадрата.
- Нарисовать прямые линии AB, BC, CD и AD, чтобы получить квадрат.
Теперь у вас есть точный и эффективный метод построения квадрата вписанного в окружность. Пользуйтесь им по своему усмотрению и наслаждайтесь результатом.
Построение центра окружности
Для определения центра окружности, необходимо разделить диагонали квадрата пополам. Для этого мы можем воспользоваться следующими техниками:
| Техника | Описание |
|---|---|
| Метод деления | Проведите прямую линию от одного угла квадрата до противоположного угла. Перпендикуляр к этой линии, проходящий через середину диагонали, будет пересекать ее пополам и определит центр окружности. |
| Метод равных отрезков | Разделите каждую из диагоналей пополам при помощи двух перпендикулярных линий. Точка пересечения этих линий будет являться центром окружности. |
| Метод проекций | На каждую диагональ проведите некоторое количество параллельных линий. Проведите перпендикуляр к этим линиям в точке пересечения диагоналей. Точка пересечения всех перпендикуляров будет центром окружности. |
Когда центр окружности определен, мы можем начать строить сам квадрат и окружность вокруг него. Помните, что для получения наиболее точного и эффективного результата, рекомендуется использовать все доступные методы определения центра окружности и выбрать наиболее точный результат.
Построение сторон квадрата
После построения центра окружности и её радиуса, можно приступить к построению сторон квадрата. Для этого нам понадобится линейка и компас.
1. Установите концентрическую окружность в центре построения.
2. Возьмите линейку и начертите линию, проходящую через центр окружности и противоположные точки на её окружности. Эта линия будет первой стороной квадрата.
3. Чтобы найти остальные стороны квадрата, найдите точку на окружности между первой и третьей четвертями (считая по часовой стрелке) и снова начертите линию, проходящую через центр окружности и эту точку. Эта линия будет второй стороной квадрата.
4. Повторите шаг 3 для точек между третьей и пятой четвертями, пятой и седьмой четвертями, а также седьмой и девятой четвертями. Каждая из этих линий станет соответствующей стороной квадрата.
Таким образом, каждая из четырех сторон квадрата будет проходить через центр окружности и противоположные точки на её окружности, образуя идеальный квадрат, точно вписанный в окружность.
Обратите внимание, что для получения более точного квадрата следует использовать большее количество точек на окружности для построения сторон квадрата.
Построение окружности
Для построения окружности необходимо знать ее центр и радиус. Центр окружности это точка, от которой все точки на окружности равноудалены. Радиус - это расстояние от центра окружности до любой точки на окружности.
В геометрии существует несколько методов построения окружности. Один из наиболее простых способов - использовать циркуль и линейку.
Для построения окружности с известным центром используйте циркуль. Установите точку циркуля в центре окружности и нарисуйте окружность, проводя линии от центра до различных точек на окружности.
При построении окружности с известным радиусом используйте линейку. Установите линейку на начальной точке окружности, а затем проведите линию равной длины радиуса, поворачивая линейку вокруг начальной точки. Нарисуйте окружность, соединяя конечную точку линии с начальной точкой окружности.
Построение окружности может быть использовано для решения различных задач в геометрии и инженерии, а также в проектировании и архитектуре.