График функции – это графическое представление зависимости одной величины от другой. Он является основным инструментом анализа и визуализации математических функций. На графике функции можно увидеть ее поведение, определить особенности, такие как экстремумы, асимптоты, пересечения с осями и другие важные характеристики.
Однако, в некоторых случаях можно представить график функции без точек. Это может быть полезно, если функция не определена на некоторых точках или если ее значения не имеют особой значимости для анализа. График функции без точек – это абстрактное представление ее формы и свойств, которое позволяет сосредоточиться на общих закономерностях и понять ее поведение в целом.
В данном руководстве мы рассмотрим основные принципы построения графика функции без точек. Мы научимся интерпретировать этот абстрактный график и использовать его для анализа и понимания функции. Помимо того, мы рассмотрим различные типы функций и их графиков без точек, чтобы показать, что такой подход может быть эффективным инструментом исследования разных математических моделей и задач.
Чем быстрее решить график функции без точек, тем лучше

Однако, чтобы решить график функции без точек, вам может понадобиться некоторая работа и практика. Вам придется изучить основные принципы построения графиков функций, а также научиться работать с различными типами функций. Например, функции линейного роста, квадратичные функции, показательные функции и т.д.
Ключевым навыком, который нужно развить, является умение анализировать функции и определять их особенности. Например, нули функции, точки перегиба, асимптоты и экстремумы. Все эти понятия играют важную роль в построении графиков функций и помогают нам понять их поведение.
Быстрое решение графика функции без точек имеет свои преимущества. Во-первых, это сэкономит ваше время и позволит сосредоточиться на других важных задачах. Во-вторых, быстрое решение графика функции без точек поможет вам лучше понять суть задачи и основные принципы ее решения.
Однако, не стоит забывать, что скорость не всегда является главным фактором. Важно учесть все детали и правильно проанализировать функцию, чтобы получить точный и полный график. Запомните, что качество всегда важнее скорости.
Обзор графика функции без точек и преимущества его решения
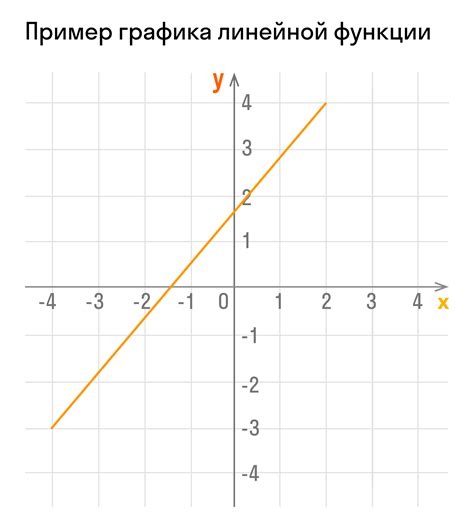
График функции без точек представляет собой графическое представление функции, где точки на графике проектируются прямой линией, вместо отдельных точек. Такой подход к построению графика функции имеет свои преимущества и может быть особенно полезен для начинающих.
Одним из основных преимуществ графика функции без точек является его удобный и наглядный способ представления информации. Построение графика функции в таком формате позволяет наглядно увидеть основные свойства функции, такие как её рост, убывание, точки перегиба, асимптоты и другие важные характеристики.
Кроме того, использование графика функции без точек позволяет легко сравнивать и анализировать несколько функций одновременно. Например, при сравнении двух функций на одном графике можно быстро определить их пересечение и точки экстремума, что помогает в решении различных математических задач и проведении компаративного анализа.
Ещё одним преимуществом графика функции без точек является его компактность. Благодаря отсутствию отдельных точек, график функции с линейной проекцией занимает меньше пространства на странице и позволяет легко вписывать дополнительные элементы, такие как подписи к осям координат, скользящие средние и другие дополнительные данные.
И наконец, график функции без точек является удобным инструментом для визуализации математических функций различной сложности. Такой тип графика может быть использован как в учебных целях, так и в профессиональной деятельности, включая научные и инженерные исследования, а также для отображения экономических и статистических данных.
В целом, график функции без точек представляет собой удобный, наглядный и компактный инструмент для визуализации функций, который обладает рядом преимуществ и может быть особенно полезен для начинающих в изучении математических функций.
Как решить график функции без точек: пошаговое руководство

Чтобы составить график функции без точек, следуйте этому пошаговому руководству:
| Шаг 1: | Определите диапазон аргументов, для которых вы хотите построить график функции. Найдите минимальное и максимальное значение аргумента. |
| Шаг 2: | Выберите интервал для шага изменения аргумента. Например, вы можете выбрать шаг 1, в котором аргумент будет изменяться на 1 единицу, или меньший шаг для более детального графика. |
| Шаг 3: | Для каждого значения аргумента в заданном диапазоне вычислите соответствующее значение функции. Это может потребовать использования алгоритмов или формул для сложных математических функций. |
| Шаг 4: | Постройте таблицу значений, в которой каждая строка представляет собой пару значений (аргумент и значение функции). Упорядочите строки в порядке возрастания аргумента. |
| Шаг 5: | Используя полученные значения, нарисуйте график функции. Постройте оси координат, отметьте значения аргументов на оси абсцисс и значения функции на оси ординат. Соедините точки линиями для создания графика функции. |
| Шаг 6: | Добавьте подписи осей и заголовок для графика функции. Убедитесь, что все значения и метки четко видны и понятны. |
Следуя этому пошаговому руководству, вы сможете легко и точно построить график функции без точек и проанализировать ее поведение в заданном диапазоне аргументов.