Построение графика функции - важный навык, который поможет понять и визуализировать зависимость между значениями переменных. В 7 классе алгебры линейной ученики начинают изучать эту тему, поэтому она является одной из основных в программе этого класса.
Для построения графика функции необходимо знать алгебраическое выражение функции, которое описывает ее зависимость. Функция может задаваться различными способами: например, через формулу, таблицу значений или графически.
Наиболее распространенный способ построения графика функции - это использование координатной плоскости. Оси OX и OY разделяют плоскость на четыре части, называемые четвертями. Каждая четверть имеет свою характеристику: в первой четверти положительные значения обоих координат, во второй - отрицательное значение координаты Y и положительное значение координаты Х, и так далее.
Построение графика функции - это последовательное отображение значений функции на координатной плоскости при помощи точек, которые соединяются линиями. Каждая точка на графике соответствует определенному значению переменных. Для удобства можно использовать таблицу значений: записать значения переменных X и соответствующие им значения Y.
Определение графика функции
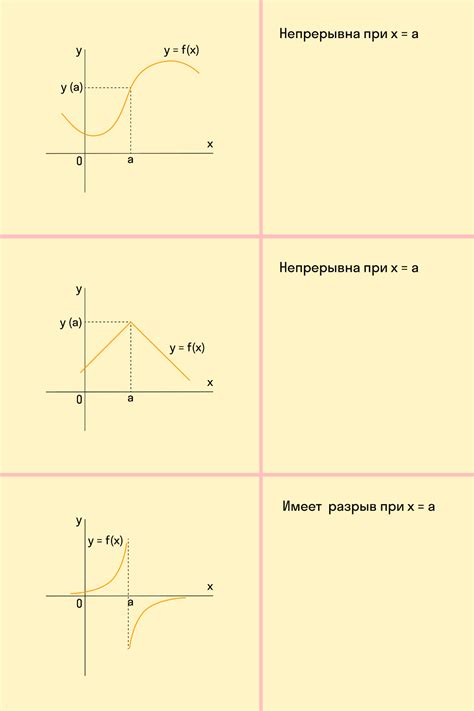
График функции строится на прямоугольной координатной плоскости, где оси X и Y представляют значения переменных функции. Ось X называется горизонтальной, а ось Y - вертикальной. На оси X откладываются значения независимой переменной, а на оси Y - значения зависимой переменной.
Для построения графика функции необходимо знать значения функции при различных значениях переменных. Пары значений обеих переменных отображаются на плоскости точками. Затем эти точки соединяются прямыми или кривыми линиями, образуя график функции.
| X | Y |
|---|---|
| -3 | 4 |
| -2 | 1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 4 |
Например, для функции Y = X^2 + 1, с использованными значениями X и соответствующими значениями Y, график будет представлен точками и линиями, образующими кривую параболу.
Значение графика функции в алгебре линейной
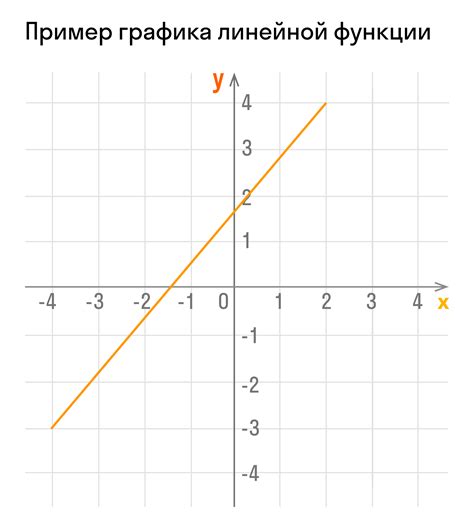
Для построения графика функции необходимо знать ее уравнение и область определения. Уравнение функции задает правило, по которому каждому значению аргумента соответствует значение функции. Область определения определяет значения аргументов, для которых функция определена.
Построение графика функции начинается с выбора некоторых значений аргумента из области определения. Затем для каждого выбранного значения аргумента вычисляют значение функции. Пары значений аргумента и значения функции образуют точки на графике функции.
Для построения графика функции можно использовать таблицу значений. В этой таблице столбцы представляют значения аргумента и значения функции, а строки соответствуют различным значениям аргумента. На основе таблицы значений можно построить график функции, отображая точки на координатной плоскости.
График функции отражает ее основные свойства, такие как возрастание и убывание, экстремумы, асимптоты и пересечение с осями координат. Анализируя график функции, можно определить ее поведение в различных интервалах значений аргумента и принять решение о ее использовании в решении задачи.
Как выбрать функцию для построения графика в 7 классе?

Для того чтобы выбрать функцию для построения графика, необходимо понять, как она будет выглядеть на координатной плоскости. Один из способов это сделать - присвоить различные значения переменной x и вычислить соответствующие значения y. Затем можно построить таблицу со значениями x и y и посмотреть на закономерности в этих данных. Например, если значения y возрастают с увеличением значения x, то график будет возрастающей прямой.
Другим способом выбора функции является установление связи между задачей и графиком. Например, если задача имеет геометрическую интерпретацию, то функция может описывать зависимость координат точек на плоскости. Если задача связана с движением объекта, то функция может описывать зависимость времени и пути.
Необходимо также учитывать, что выбранная функция должна быть доступной для построения графика. Для учащихся 7 класса рекомендуется выбирать простые функции, у которых значения k и b малы и легко поддаются вычислению без использования калькулятора.
Наконец, при выборе функции для построения графика необходимо учитывать цель задания и то, какая информация должна быть наглядно представлена на графике. Например, для отображения зависимости между двумя величинами наиболее удобными функциями являются линейные функции, так как они просты и понятны для восприятия.
В итоге, выбор функции для построения графика в 7 классе зависит от контекста и цели задачи. Необходимо анализировать задачу, установить связь между задачей и графиком, и выбрать функцию, которая является наиболее подходящей для этой задачи.
Важные понятия для построения графика функции
Для построения графика функции необходимо знать и правильно применять несколько важных понятий. Они помогут нам ориентироваться на координатной плоскости и строить точки, соответствующие значениям функции.
Первое понятие - это система координат. Координатная плоскость состоит из двух осей - горизонтальной оси OX и вертикальной оси OY. Они пересекаются в точке O, которая называется началом координат. По горизонтальной оси откладываются значения аргумента функции (обычно это числа), а по вертикальной оси - значения самой функции.
Далее, нужно понять, что такое функция. Функция - это правило, которое ставит в соответствие каждому значению аргумента определенное значение функции. Обозначается функция обычно символом f, например f(x). То есть, мы подставляем значение аргумента x в функцию f и получаем значение функции.
Для построения графика функции мы должны знать ее соотношение с аргументами и значениями функции. Если функция задана в виде алгебраической формулы, то можем оценить ее поведение на графике. Например, если функция имеет вид f(x) = ax + b, то график будет представлять собой прямую линию.
Еще одним важным понятием является точка на графике функции. Точка на графике представляет собой пару значений (x, f(x)), где x - значение аргумента, а f(x) - значение функции. Эти точки соединяются линиями, которые образуют график функции.
Итак, для построения графика функции необходимо знать систему координат и понимать, как задана функция и как связаны значения аргумента и функции. Зная эти основные понятия, мы сможем построить график функции и проанализировать ее поведение.
Построение осей координат и их значения
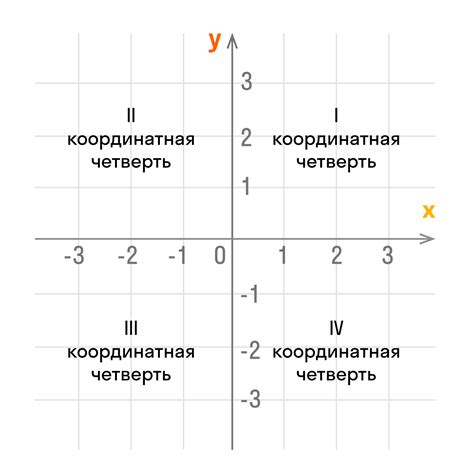
Чтобы построить график функции, нам необходимо сначала построить оси координат.
Для этого нужно:
- Нарисовать две взаимно перпендикулярные прямые, которые будут являться осями абсцисс и ординат.
- Отметить на оси значения. Для этого выберем шаг, с которым будем отмечать значения. Например, если мы выбрали шаг равным 1, то на оси абсцисс будут отмечены значения 1, 2, 3 и так далее, а на оси ординат – значения 1, 2, 3 и так далее.
- Подписать оси абсцисс и ординат. Обычно используются буквы OX и OY соответственно.
После построения осей координат, мы можем приступить к построению графика функции.
Построение точек на графике функции
Поэтапное построение графика функции включает в себя определение значений функции для различных значений аргумента и отображение этих точек на плоскости.
Для начала, необходимо выбрать оси координат и задать масштаб, чтобы удобно было отображать значения функции. Ось абсцисс (OX) графика соответствует значениям аргумента функции, а ось ординат (OY) – значениям функции.
Далее, по заданным значениям аргумента из выбранного диапазона, необходимо построить соответствующие значения функции. Для этого выполняется подстановка аргументов в функцию и вычисление значений. Полученные значения представляются точками на графике.
Точки на графике можно обозначить разными способами, например, с помощью точек, кружков или квадратиков. Каждая точка должна быть помечена с указанием координат – значение аргумента и соответствующего значения функции.
Когда все точки функции построены, их можно соединить линией, чтобы получить гладкую кривую графика функции.
Построение точек на графике функции позволяет лучше представить себе взаимосвязь между аргументом и значением функции. Это помогает анализировать поведение функции, находить ее особенности и решать задачи на основе графического представления функции.
Соединение точек линиями

Когда мы строим график функции в алгебре, нам необходимо соединить точки на координатной плоскости. Для этого мы используем линии, которые соединяют точки и помогают нам визуализировать функцию.
Соединение точек линиями позволяет нам видеть плавное изменение функции между точками и анализировать ее поведение. Например, если функция возрастает, то линия будет идти вверх, а если функция убывает, то линия будет идти вниз.
Очень важно правильно соединять точки линиями, чтобы избежать путаницы при анализе функции. Как правило, мы используем прямые линии между точками, если функция непрерывна. Если же функция разрывна, то мы используем перерывные линии или точечные маркеры.
При соединении точек линиями, мы также учитываем направление осей координат. Обычно горизонтальная ось соединяет точки слева направо, а вертикальная ось соединяет точки сверху вниз.
Итак, соединение точек линиями помогает нам построить график функции и анализировать ее поведение. Это важный навык в алгебре, который открывает перед нами множество возможностей для изучения и понимания математических функций.
Как определить вид и характеристики графика функции?

Вид графика функции: Для определения вида графика функции необходимо проанализировать ее алгебраическое выражение. Следующие категории графиков часто встречаются при изучении алгебры:
| Вид графика | Пример функции |
| Прямая | y = kx + b, где k и b - константы |
| Парабола | y = ax^2 + bx + c, где a, b и c - константы, a ≠ 0 |
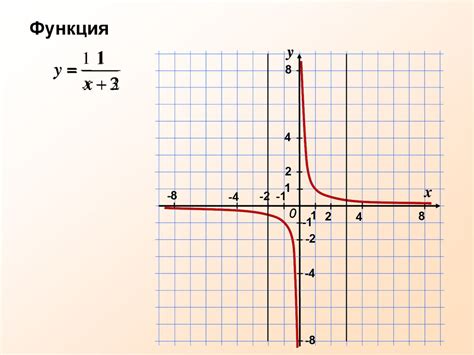
| Гипербола | y = a/x, где a - константа, a ≠ 0 |
| Экспоненциальная функция | y = a^x, где a - константа, a > 0, a ≠ 1 |
Характеристики графика функции: Визуальный анализ графика функции позволяет определить некоторые важные характеристики:
- Наклон: Угол наклона прямой может быть положительным (восходящая линия), отрицательным (нисходящая линия) или равным нулю (горизонтальная линия).
- Точка пересечения с осями: График функции пересекает ось x в точке, где y = 0, и ось y в точке, где x = 0.
- Точка экстремума: Экстремум (максимум или минимум) функции находится в точке, где график функции меняет свое направление.
- Асимптоты: Асимптоты графика функции - прямые, которые график функции стремится приблизиться, но никогда не пересекает.
С помощью анализа функции и ее графика можно получить много информации о ее поведении и свойствах. Построение графика функции и определение его характеристик позволяет не только лучше понять функцию, но и применять полученные знания в решении математических задач.