Построение графиков функций является одной из важных тем в алгебре. Графики помогают наглядно представить функции и изучать их свойства. Все это становится особенно интересным, когда мы изучаем функции первой степени, такие как функция y = 2x + 1.
Функция y = 2x + 1 представляет собой линейную функцию, которую можно представить графически с помощью прямой линии на плоскости. Чтобы построить график этой функции, необходимо найти несколько точек, через которые проходит линия.
Для этого можно выбрать любые значения для переменной x и подставить их в уравнение функции. Например, можно взять x = 0 и x = 1. Подставив эти значения, мы получим соответствующие значения для y. Таким образом, мы получим две точки: (0, 1) и (1, 3).
Алгоритм для построения графика функции y = 2x + 1
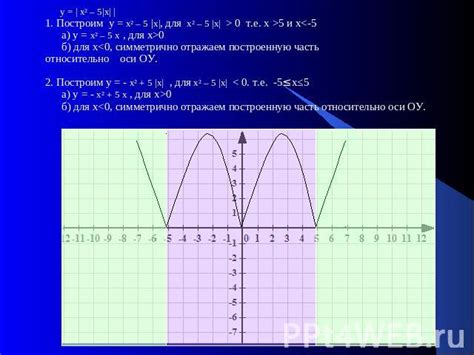
Для построения графика функции y = 2x + 1 в алгебре 7 класс, можно следовать следующему алгоритму:
| № | x | y = 2x + 1 |
|---|---|---|
| 1 | -2 | -3 |
| 2 | -1 | -1 |
| 3 | 0 | 1 |
| 4 | 1 | 3 |
| 5 | 2 | 5 |
Сначала выберите несколько значений для переменной x и вычислите соответствующие значения для переменной y. Например, мы взяли значения -2, -1, 0, 1 и 2 для x и, затем, вычислили значения для y, используя функцию y = 2x + 1.
Затем постройте график, используя полученные значения. Для этого, на горизонтальной оси отложите значения переменной x, а на вертикальной оси отложите значения переменной y. Найдите точки с соответствующими координатами на графике и соедините их линией.
В нашем примере, полученные значения (x, y) для функции y = 2x + 1: (-2, -3), (-1, -1), (0, 1), (1, 3) и (2, 5). Построим график, соединив эти точки линией. Получится наклонная прямая, идущая вверх и направленная вправо.
Таким образом, можно построить график функции y = 2x + 1, следуя данному алгоритму.
Определение значений для x

Чтобы построить график функции y = 2x + 1, необходимо определить значения для переменной x. Для этого можно выбрать произвольные числа и подставить их вместо x, чтобы получить соответствующие значения для y.
Например, можно выбрать x = 0 и подставить его в уравнение функции: y = 2 * 0 + 1 = 1. Это означает, что при x = 0, значение y будет равно 1. Далее можно выбрать другие значения для x и вычислить соответствующие значения для y, например, x = 1: y = 2 * 1 + 1 = 3. Таким образом, при x = 1, значение y будет равно 3.
Чтобы построить график функции, можно продолжить этот процесс выбора различных значений для x и вычисления соответствующих значений для y. Результаты можно представить в виде таблицы или списке, где для каждого значения x указывается соответствующее значение y.
Например:
- x = 0, y = 1
- x = 1, y = 3
- x = 2, y = 5
- x = 3, y = 7
- и т.д.
Затем, используя полученные значения для x и y, можно построить график, где по оси x откладываются значения для x, а по оси y - значения для y. Постепенно соединяя полученные точки, можно получить график функции y = 2x + 1.
Вычисление соответствующих значений для y
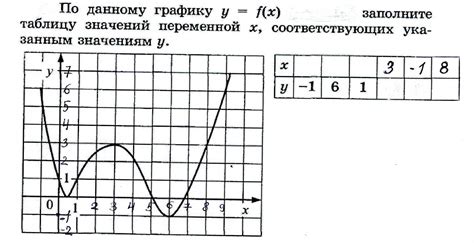
Для построения графика функции y = 2x + 1 необходимо вычислить соответствующие значения для переменной y при различных значениях переменной x.
Сначала выбираем произвольное значение для x, например, x = 0. Подставляем это значение в уравнение функции и выполняем вычисления:
y = 2 * 0 + 1 = 1
Таким образом, при x = 0 значение функции равно y = 1.
Далее выбираем другое значение для x, например, x = 1, и проводим вычисления:
y = 2 * 1 + 1 = 3
Получаем, что при x = 1 значение функции равно y = 3.
Аналогично вычисляются и остальные значения функции для различных значений переменной x. Полученные значения образуют точки на графике функции.
Построение графика на координатной плоскости
Чтобы построить график функции на координатной плоскости, нужно выполнить следующие шаги:
- Определить интервал значений для переменной x, на котором будет строиться график. Для этого часто используются значения переменной x в диапазоне -10 до 10.
- Подставить каждое значение переменной x в функцию и вычислить соответствующее значение переменной y. Например, при x = 0: y = 2(0) + 1 = 1. При x = 1: y = 2(1) + 1 = 3 и т.д.
- Полученные значения точек (x, y) записать в таблицу.
- На координатной плоскости построить оси x и y, выбрав удобный масштаб. Например, можно выбрать шаг 1 по оси x и шаг 1 по оси y.
- Отметить на оси x и y значения согласно выбранному масштабу.
- По полученным значениям из таблицы построить точки на графике, где x-координатой будет значение переменной x, а y-координатой - значение переменной y.
- Соединить полученные точки прямой.
Таким образом, построение графика функции y = 2x + 1 на координатной плоскости позволяет наглядно представить зависимость переменной y от переменной x и увидеть соотношение между ними.