Графики функций имеют важное значение в математике и применяются в различных областях, включая физику, экономику и инженерные науки. Квадратичная функция является одной из наиболее распространенных и изучаемых функций в алгебре и аналитической геометрии.

Квадратичная функция имеет вид f(x) = ax^2 + bx + c, где a, b и c - коэффициенты. Зная значения этих коэффициентов, мы можем построить график функции на плоскости.

Процесс конструирования графика квадратичной функции включает в себя ряд шагов. Во-первых, мы определяем вершину графика, которая находится в точке (-b/2a, f(-b/2a)). Затем мы находим значения функции для нескольких точек слева и справа от вершины, используя значения x, близкие к (-b/2a). Подставляя эти значения x в уравнение квадратичной функции, мы находим соответствующие значения y. Используя полученные координаты точек, мы можем построить график на координатной плоскости.

Примерами квадратичных функций могут служить функции вида f(x) = x^2, f(x) = 2x^2 - x + 3, f(x) = -3x^2 + 4x - 1 и другие. Для каждой функции соответствующий график будет иметь свои особенности и форму. Например, график функции f(x) = x^2 будет представлять собой параболу, являющуюся осью симметрии ветвей графика.

Конструирование графика квадратичной функции

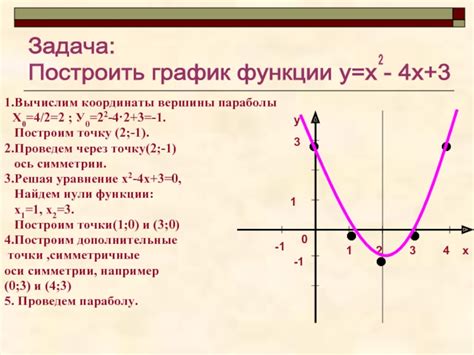
График квадратичной функции представляет собой параболу, которая может быть выпуклой вверх или вниз. Для построения графика необходимо знать основные характеристики функции, такие как вершина параболы, направление выпуклости, а также поведение функции на бесконечности.

Алгоритм построения графика квадратичной функции может быть следующим:

1. Найти вершину параболы, которая является точкой максимума или минимума функции.
2. Определить направление параболы. Если коэффициент при переменной x в квадратичном члене функции положителен, парабола будет выпуклой вверх, если отрицателен - выпуклой вниз.
3. Построить ось симметрии параболы, которая проходит через вершину и является перпендикулярной оси x.
4. Определить поведение функции на бесконечности. Если старший коэффициент функции положителен, то при x → ±∞ функция также стремится к +∞. Если старший коэффициент отрицателен, то при x → ±∞ функция стремится к -∞.
5. Построить график, используя полученные характеристики pараболы и свойства функции.

Определение вершины параболы и ее направление выпуклости основано на формуле квадратичной функции:

f(x) = ax² + bx + c

Вершина параболы имеет координаты (h, k), где:

h = -b/(2a), k = f(h)

Если коэффициент a положителен, то парабола будет выпуклой вверх, если a отрицателен - выпуклой вниз.

Построение графика квадратичной функции является ключевым шагом при анализе данного типа функций. Следуя описанному алгоритму, можно легко определить основные характеристики функции и построить график, что помогает в понимании ее поведения и в решении задач, связанных с квадратичными функциями.

Принципы и примеры

Для построения графика квадратичной функции необходимо выполнить следующие шаги:

1. Определить основные характеристики функции, такие как дискриминант, вершина параболы и направление ее ветвей.
2. Найти несколько значений x и вычислить соответствующие значения y с использованием уравнения функции.
3. Составить таблицу с найденными значениями и построить график, отображая точки на координатной плоскости.
4. Продолжить процесс, находя дополнительные точки для большей точности и понимания формы графика.

Пример:

Дана функция y = 2x^2 - 3x + 1. Найдем значение дискриминанта:

D = b^2 - 4ac

D = (-3)^2 - 4 * 2 * 1 = 9 - 8 = 1

Так как дискриминант положительный, у нас будет одна реальная вершина параболы.

Найдем координаты вершины:

x = -b / (2a) = -(-3) / (2 * 2) = 3 / 4

y = ax^2 + bx + c = 2 * (3/4)^2 - 3 * (3/4) + 1 = 9/8 - 9/4 + 1 = 9/8 - 18/8 + 8/8 = 1/8

Таким образом, вершина параболы находится в точке (3/4, 1/8).

Построим график, используя полученные данные и дополнительные значения:

• Если x = 0, то y = 1 (координаты точки (0, 1)).
• Если x = 1, то y = 0 (координаты точки (1, 0)).
• Если x = 2, то y = 1 (координаты точки (2, 1)).
• ...

Подключив все полученные точки, мы можем нарисовать параболу, отобразив ее ветви и ее ось симметрии на графике.

Алгоритм построения графика

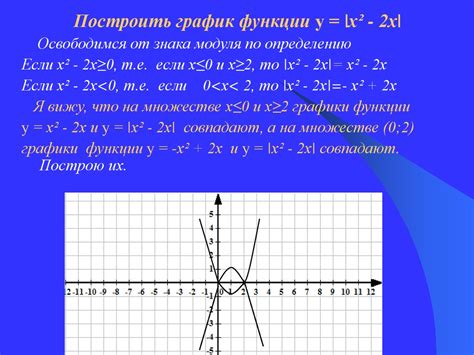
Построение графика квадратичной функции требует выполнения ряда шагов, чтобы точно определить форму и положение графика на координатной плоскости.

Шаг 1: Определите форму функции, проверьте коэффициенты.

Для начала убедитесь, что у вас есть квадратичная функция вида y = ax^2 + bx + c, где a, b и c - коэффициенты, которым присвоены числовые значения.

Коэффициент a определяет, насколько быстро функция меняется в конкретном направлении.

Коэффициент b определяет, насколько быстро функция сдвигается вперед или назад (горизонтальное смещение по оси y).

Коэффициент c представляет собой вершину (минимум или максимум) функции и определяет вертикальное смещение.

Шаг 2: Найдите вершину функции.

Чтобы найти вершину функции, используйте формулу x = -b / (2a). Затем подставьте значение x обратно в уравнение, чтобы найти y.

Шаг 3: Найдите ось симметрии.

Ось симметрии функции проходит через вершину. Ось параллельна оси y и имеет координаты (x, y), где x - координата вершины, а y - значение, соответствующее x.

Шаг 4: Постройте график функции.

С использованием найденных координат вершины и оси симметрии, нарисуйте параболу, которая будет иметь форму, определенную коэффициентами a, b и c.

При построении графика учтите, что если коэффициент a положительный, парабола будет направлена вверх, в противном случае, если a отрицательный, парабола будет направлена вниз.

Используйте найденные координаты вершины и оси симметрии, чтобы отметить точки на графике и примерно нарисовать форму функции.

Основные характеристики квадратичной функции

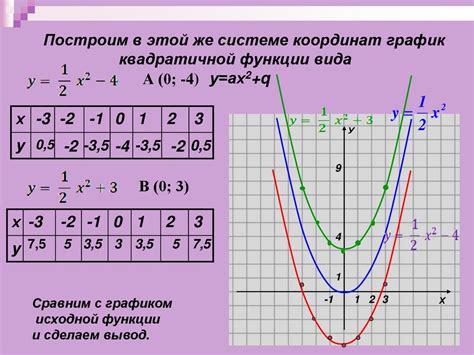
Основные характеристики квадратичной функции включают:

1. Вершина. Вершина графика квадратичной функции имеет координаты (-b/2a, f(-b/2a)). Вершина может быть наименьшей или наибольшей точкой графика, в зависимости от знака коэффициента a.
2. Ось симметрии. Ось симметрии графика квадратичной функции является вертикальной прямой, проходящей через вершину. Функция симметрична относительно этой оси, что значит, что значения функции с обоих сторон равны при одинаковом удалении от оси симметрии.
3. Направление ветвей. Направление ветвей графика квадратичной функции зависит от знака коэффициента a. Если a > 0, ветви направлены вверх, а если a
4. Пересечение с осями. График квадратичной функции может пересекать ось OX в двух точках, одной точке или не пересекать ее вовсе. Пересечение с осью OY происходит в точке с координатами (0, c), где c - свободный член функции.

Знание этих основных характеристик квадратичной функции позволяет легче конструировать ее график и анализировать ее свойства. Кроме того, они также могут использоваться для нахождения дополнительной информации о функции, такой как экстремумы, интервалы возрастания и убывания и другие важные моменты.

Применение графика квадратичной функции в реальной жизни

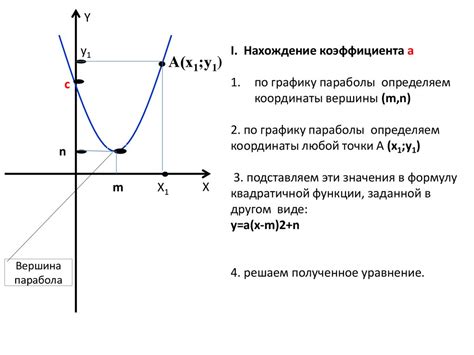
В физике график квадратичной функции может быть использован для моделирования траектории движения объекта под действием гравитации или других сил. Например, график квадратичной функции может описывать полет снаряда или движение автомобиля под действием силы трения и сопротивления воздуха.

В инженерии график квадратичной функции может быть использован для оптимизации процессов и расчета траекторий. Например, при проектировании моста или ракеты, график квадратичной функции может помочь определить наиболее эффективные параметры конструкции.

В экономике график квадратичной функции может быть использован для анализа зависимости между двумя переменными, такими как цена и количество продукции. График позволяет определить точки экстремума, что может быть полезно при принятии управленческих решений.

В биологии график квадратичной функции может быть использован для моделирования эволюционных процессов или распределения популяции в зависимости от времени или окружающих условий.

В целом, график квадратичной функции играет важную роль в научных и практических приложениях, помогая нам лучше понимать и описывать сложные явления и процессы в реальном мире.