Построение графиков тригонометрических функций является важной задачей в математике и физике. Одним из ключевых аспектов при построении графиков является учет смещения функции. Смещение позволяет изменить положение функции на графике, что может быть полезно, например, при анализе периодических явлений.
Для того чтобы построить график тригонометрической функции со смещением, следует использовать следующие шаги:
- Определить базовую функцию и ее параметры. Базовая функция - это функция без каких-либо изменений. Например, базовой функцией для синусоиды может быть функция y = sin(x).
- Определить значение смещения по оси x и оси y. Смещение по оси x может быть задано как положительное или отрицательное число, а смещение по оси y - как число, определяющее вертикальное смещение функции.
- Применить смещение к базовой функции. Для смещения по оси x следует добавить или вычесть значение смещения из аргумента функции. Для смещения по оси y следует добавить или вычесть значение смещения из значения функции.
- Построить график измененной функции. Для этого следует выбрать значения аргумента функции в заданном интервале, вычислить соответствующие значения функции и отобразить их на графике.
Например, если нам необходимо построить график функции y = sin(x) со смещением по оси x на 2 и по оси y на -1, то мы должны применить смещение и построить график измененной функции y = sin(x - 2) - 1.
В результате выполнения этих шагов мы получим график тригонометрической функции со смещением, который поможет нам лучше понять и анализировать данное явление или процесс.
Разбор основных понятий

Перед тем, как перейти к построению графика тригонометрической функции со смещением, необходимо разобраться в некоторых основных понятиях.
Тригонометрическая функция - это функция, которая отображает отношение сторон прямоугольного треугольника в соответствии с углами этого треугольника. Наиболее распространенные тригонометрические функции - синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg).
Смещение (перенос, сдвиг) графика тригонометрической функции - это изменение его положения на координатной плоскости. С помощью смещения можно сдвинуть график вправо или влево, а также вверх или вниз.
Для построения графика тригонометрической функции со смещением необходимо знать значения основных точек графика (амплитуда, период и фазовый сдвиг) и применить соответствующие преобразования координат.
Амплитуда - это максимальное значение функции. Она определяет вертикальный масштаб графика.
Период - это расстояние между двумя соседними повторяющимися точками графика. Он определяет горизонтальный масштаб графика.
Фазовый сдвиг - это горизонтальное смещение графика влево или вправо относительно исходной функции. Он определяет, насколько график сдвинут по горизонтальной оси.
Используя эти основные понятия, можно построить график тригонометрической функции со смещением и более точно представить изменения, происходящие с функцией в зависимости от изменения ее параметров.
Функция

Тригонометрическая функция представляет собой математическую функцию, которая зависит от угла. График этой функции имеет периодическую форму и может быть представлен в виде волн или колебаний.
Наиболее известными тригонометрическими функциями являются синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec) и косеканс (cosec). Каждая из этих функций имеет свои уникальные свойства и характеристики.
Тригонометрические функции широко используются в различных областях науки, инженерии и физике, так как они являются основой для описания колебательных процессов и циклических явлений.
Для построения графика тригонометрической функции со смещением необходимо применить соответствующие формулы и методы. Смещение может быть выполнено по горизонтали (сдвиг влево или вправо) или вертикали (сдвиг вверх или вниз). Эти смещения могут изменять период и амплитуду функции.
Учитывая свойства и характеристики тригонометрических функций, а также используя правильные формулы и методы, можно построить график функции с высоким уровнем точности, что поможет в изучении и анализе различных явлений и процессов, описываемых этими функциями.
Тригонометрическая функция
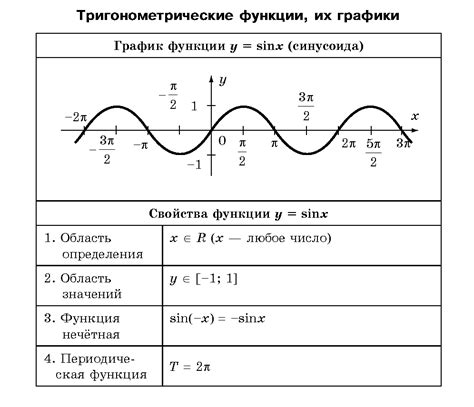
Синус угла равен отношению противоположной стороны к гипотенузе, косинус угла равен отношению прилегающей стороны к гипотенузе, а тангенс угла равен отношению противоположной стороны к прилегающей стороне. Математически они определены через соотношение сторон прямоугольного треугольника.
График тригонометрической функции представляет собой зависимость между углом и значением функции. График синусоиды (график синусной функции) имеет форму волны, которая повторяется через определенный период. График косинусоиды (график косинусной функции) также имеет форму волны, но начинает смещаться по фазе относительно графика синуса.
Чтобы построить график тригонометрической функции со смещением, необходимо знать амплитуду, период и фазу функции. Амплитуда отвечает за величину колебаний функции, период - за расстояние между двумя соседними повторениями графика волны, а фаза определяет сдвиг графика по горизонтальной оси.
Для построения графика можно использовать графический редактор, программы для создания графиков, или математические пакеты, такие как MATLAB или Python с библиотеками для графиков. Построение графиков тригонометрических функций с использованием этих инструментов обеспечивает точность и визуальное представление функции со смещением.
Определение графика тригонометрической функции
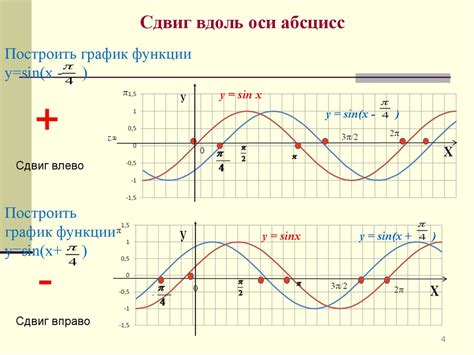
График тригонометрической функции представляет собой графическое представление зависимости между углом и значением функции. Тригонометрические функции, такие как синус, косинус, тангенс и их обратные функции, широко используются в математике, физике и других науках.
График тригонометрической функции обычно строится в прямоугольной системе координат, где значение функции откладывается по вертикальной оси, а угол - по горизонтальной оси. В случае синуса и косинуса, значения функции находятся в диапазоне от -1 до 1.
На графике можно наблюдать периодичность, амплитуду, фазовый сдвиг и другие характеристики функции. Периодичность означает, что функция повторяется через определенный интервал углов, например, 2π (в радианах) или 360° (в градусах). Амплитуда определяет максимальное значение функции. Фазовый сдвиг отражает горизонтальное смещение графика функции.
Построение графика тригонометрической функции со смещением требует изменения амплитуды и фазового сдвига. Для этого используются соответствующие формулы преобразования. Например, для графика синуса, амплитуда задается множителем перед функцией, а фазовый сдвиг - добавлением или вычитанием значения в аргументе функции.
Необходимые инструменты

Для построения графика тригонометрической функции со смещением вам потребуются следующие инструменты:
- Калькулятор с тригонометрическими функциями: синус, косинус, тангенс;
- Графический редактор или программное обеспечение для построения графиков;
- Бумага и карандаш для ручного построения графика (опционально);
- Компьютер или ноутбук с доступом к интернету для использования онлайн-ресурсов;
Калькулятор с тригонометрическими функциями поможет вам вычислить значения функций для разных углов. Графический редактор или программное обеспечение для построения графиков позволит вам визуализировать график функции на компьютере. Бумага и карандаш могут пригодиться, если вы предпочитаете ручное построение графиков. Использование компьютера с доступом к интернету также полезно для изучения дополнительных материалов и поиска онлайн-ресурсов для построения графиков.
Графический калькулятор
Для построения графика тригонометрической функции со смещением существует несколько способов использования графического калькулятора. Во-первых, можно использовать предустановленные функции, которые часто включают встроенные функции для тригонометрических функций, такие как синус, косинус и тангенс.
Второй способ заключается в использовании возможностей графического калькулятора для манипулирования смещением и масштабированием графика функции. Для этого можно воспользоваться функцией "смещение", чтобы изменить положение графика функции на плоскости. Также можно использовать функцию "масштабирование", чтобы изменить масштаб графика и увеличить или уменьшить его размер.
Кроме того, графический калькулятор может предлагать возможность настройки осей координат и добавления различных элементов на график, таких как точки перегиба, асимптоты или экстремумы функции.
В итоге, с помощью графического калькулятора можно визуализировать график тригонометрической функции со смещением и наглядно представить ее поведение на плоскости. Это позволяет лучше понять, как функция меняется в зависимости от значений переменных и использовать эту информацию для решения задач или анализа математических моделей.
Координатная плоскость
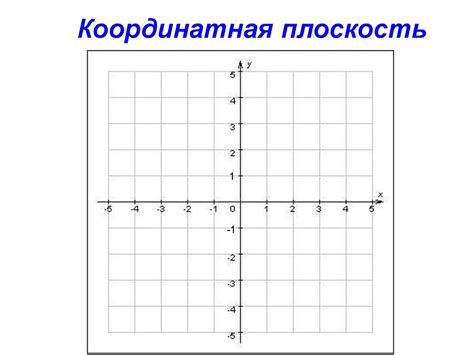
Для построения графика тригонометрической функции со смещением нам понадобится координатная плоскость. Координатная плоскость представляет собой двумерное пространство, где каждая точка имеет свои координаты.
В основе координатной плоскости лежат две перпендикулярные оси: горизонтальная ось, называемая осью абсцисс (или осью x), и вертикальная ось, называемая осью ординат (или осью y). Ось абсцисс делит плоскость на две половины: положительную (справа от оси) и отрицательную (слева от оси). Ось ординат также делит плоскость на две половины: положительную (вверх от оси) и отрицательную (вниз от оси).
Все точки на плоскости можно задать парой чисел в формате (x, y), где x - это значение на оси абсцисс, а y - это значение на оси ординат.
Для построения графика тригонометрической функции со смещением, мы будем использовать основную функцию (например, синус или косинус) и применять к ней смещения по горизонтали и вертикали. Горизонтальное смещение задается изменением значения на оси абсцисс, а вертикальное смещение - изменением значения на оси ординат. После применения смещений, мы соединяем получившиеся точки и получаем график функции.
Используя координатную плоскость, мы сможем наглядно представить смещения и визуализировать график тригонометрической функции.
Построение графика
Для построения графика тригонометрической функции со смещением требуется некоторая подготовка и использование математических формул. Следующие шаги помогут вам построить график:
- Определите амплитуду, период, фазовый сдвиг и вертикальное смещение функции. Они определяют, как будет выглядеть график.
- Найдите значения x, для которых будет строиться график. Можно выбрать диапазон значений x, чтобы получить полный обзор функции.
- Определите значения y для выбранных значений x, используя соответствующую тригонометрическую функцию.
- Постройте таблицу, в которой будут указаны значения x и соответствующие значения y.
- На основе таблицы постройте график, где по оси x отложены значения x, а по оси y отложены значения y.
- Подпишите оси графика и добавьте дополнительные элементы, если необходимо, чтобы сделать график более понятным и информативным.
Таким образом, следуя этим шагам, вы сможете построить график тригонометрической функции со смещением и получить визуальное представление о ее поведении и особенностях.
Приведенная ниже таблица может помочь вам понять, какие значения y соответствуют определенным значениям x:
| x | y |
|---|---|
| x1 | y1 |
| x2 | y2 |
| x3 | y3 |
| ... | ... |
Шаг 1: Определение амплитуды
Для определения амплитуды необходимо знать коэффициент а в уравнении функции вида y = a*sin(bx - c) + d или y = a*cos(bx - c) + d. Значение коэффициента а указывает на размах колебаний функции.
Если значение а больше 1, то функция будет иметь более выраженные колебания и амплитуда будет равна значению коэффициента. Если значение а между 0 и 1, то функция будет иметь менее выраженные колебания и амплитуда будет меньше единицы.
Если значение а отрицательное, то функция будет отражена относительно оси X и амплитуда будет равна абсолютному значению коэффициента.
Например, если уравнение функции имеет вид y = 3*sin(x), то амплитуда равна 3. Если уравнение функции имеет вид y = 0.5*cos(x), то амплитуда равна 0.5.