Desmos - это мощный онлайн-инструмент для математической визуализации, который позволяет строить графики и решать уравнения. В этом руководстве мы рассмотрим, как построить кусочную функцию в Desmos и исследовать ее свойства. Кусочные функции часто встречаются в математике и физике, а также во многих других областях науки и техники.
Кусочная функция состоит из нескольких частей, каждая из которых определена на определенном интервале. Части могут быть различных типов: линейные, квадратичные, показательные и т.д. Кусочные функции обычно используются для моделирования реальных явлений, которые не могут быть описаны одной простой функцией.
Для построения кусочной функции в Desmos необходимо разделить интервалы, на которых функция определена, и определить саму функцию для каждого интервала. Для каждого интервала можно использовать разные типы функций и задать разные параметры. Desmos позволяет строить кусочные функции с любым числом частей и исследовать их свойства, такие как непрерывность, дифференцируемость и экстремумы.
Понятие кусочной функции
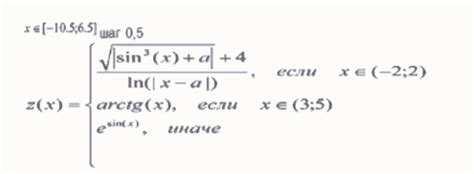
Кусочные функции широко используются в различных областях науки и техники, а также в математическом моделировании. Они позволяют описать сложные зависимости с помощью более простых формул, которые применяются на определенных участках.
Для построения кусочной функции в Desmos нужно определить формулу для каждого интервала и задать соответствующие области определения. В результате получается график, где каждый интервал имеет свою уникальную форму.
Пример:
Рассмотрим кусочную функцию:
f(x) = \left\{
\begin{array}{ll}
x, & x \leq 0 \\
x^2, & x > 0
\end{array}
ight.
В данном случае функция f(x) равна x для значений x, меньших или равных 0, и равна x^2 для значений x, больших 0. Построив эту функцию в Desmos, мы увидим график, состоящий из двух частей: прямой линии до точки (0,0) и параболы после этой точки.
Применение кусочных функций
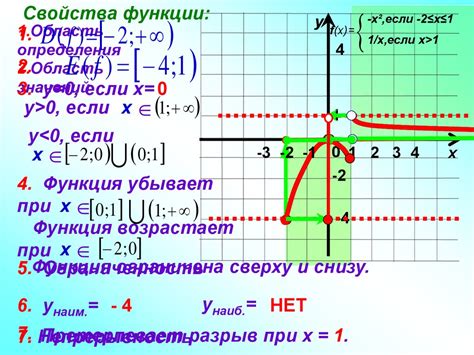
Одним из наиболее распространенных применений кусочных функций является моделирование реальных явлений и процессов. Например, кусочная функция может быть использована для представления траектории движения объекта, которая может меняться в зависимости от интервала времени или других факторов.
Кроме того, кусочные функции используются для аппроксимации сложных функций, которые трудно аналитически описать. Путем комбинирования нескольких простых функций на различных интервалах, можно достичь более точного приближения к искомой функции.
В Desmos кусочные функции могут быть построены с помощью команды "piecewise". Это позволяет задать различные функции на различных интервалах, что дает возможность создавать сложные и гибкие модели.
| Пример | Описание |
|---|---|
piecewise({x<0: x^2, x<=2: 3, x>2: 4}) | Данная кусочная функция определена следующим образом: на интервале x < 0 функция равна x^2, на интервале x <= 2 функция равна 3, а на интервале x > 2 функция равна 4. |
Применение кусочных функций позволяет создавать сложные и многофункциональные модели, которые могут быть использованы в различных областях, таких как физика, экономика, статистика и другие.
Построение кусочной функции в Desmos

Кусочная функция состоит из нескольких частей, каждая из которых определена на определенном промежутке. Обычно кусочные функции используются для моделирования реальных систем, которые могут изменяться в разных диапазонах.
Шаги для построения кусочной функции в Desmos:
- Откройте Desmos в веб-браузере и создайте новый график.
- На оси X выберите интервалы, на которых будет определена каждая часть кусочной функции. Для этого можно использовать ползунки или ввести значения вручную.
- На оси Y выберите интервалы, в которых будут находиться значения функции.
- Нажмите кнопку "Добавить экспрессию" и введите математическое выражение для каждой части кусочной функции. Например, вы можете использовать условные операторы, чтобы определить значения функции в разных диапазонах.
- При желании можно добавить описание кусочной функции, используя текстовый блок.
Desmos позволяет создавать сложные кусочные функции с различными переменными и операторами. Вы можете добавить несколько условий для определения значений функции в разных промежутках и визуализировать их на графике.
Построение кусочной функции в Desmos - это отличный способ исследовать и моделировать реальные системы, которые изменяются в разных условиях. Благодаря мощным возможностям Desmos вы сможете точно представить, как поведет себя функция в различных сценариях и изучить ее свойства.
Создание графика

Для построения кусочной функции в Desmos необходимо создать график на пустом поле координат. Чтобы начать работу, следуйте инструкциям:
- Откройте приложение Desmos на вашем устройстве или компьютере.
- Создайте новый график, щелкнув по значку «+» или выбрав соответствующую опцию в меню.
- На открывшемся поле координат введите уравнения функций. Для создания кусочной функции необходимо ввести уравнение каждого отрезка отдельно.
- Нажмите кнопку «График» или соответствующую команду, чтобы построить график функции.
- Использование дополнительных функций и параметров для настройки графика. Desmos предлагает множество возможностей для настройки графиков, таких как изменение цветов, добавление точек, настройка шкал и многое другое. Подробнее о возможностях Desmos можно узнать из документации или видеоуроков.
- Сохранение и публикация созданного графика. После того, как вы создали и настроили график, можно сохранить его или поделиться им со своими друзьями, используя соответствующие функции Desmos.
Теперь вы знаете, как создать график кусочной функции в Desmos! Это мощный инструмент, который поможет вам визуализировать и изучить различные математические концепции. Приятного использования!
Добавление условий

В Desmos вы можете добавлять условия к графикам и менять их параметры в зависимости от заданных условий.
Для добавления условия вы можете использовать операторы сравнения, такие как равно (=), больше (>), меньше (<), больше или равно (>=), меньше или равно (<=), а также логические операторы "и" (&&) и "или" (