Построение графика квадратичной функции может быть интересным и занимательным опытом. Это важный математический инструмент, который позволяет анализировать различные ситуации и прогнозировать результаты. Квадратичные функции могут быть использованы во многих областях, включая физику, экономику, компьютерную графику и многое другое.

Для построения графика квадратичной функции нам понадобится некоторая информация о самой функции. Квадратичная функция имеет вид: f(x) = ax^2 + bx + c. Здесь a, b и c - это коэффициенты, которые определяют форму и положение графика функции.

Для начала, нам нужно определить значения коэффициентов a, b и c. После этого мы можем построить таблицу значений функции, выбрав несколько значений аргумента x и вычислив соответствующие значения функции f(x). Затем мы можем построить график, отображая значения x на горизонтальной оси и значения f(x) на вертикальной оси.

Когда график готов, мы можем записать видео, чтобы показать процесс построения графика. Мы можем продемонстрировать каждый шаг, а также объяснить, какой вклад вносит каждый коэффициент в форму и положение графика. Такое видео может быть полезно и познавательно для тех, кто хочет научиться строить графики квадратичных функций самостоятельно.

Как определить квадратичную функцию

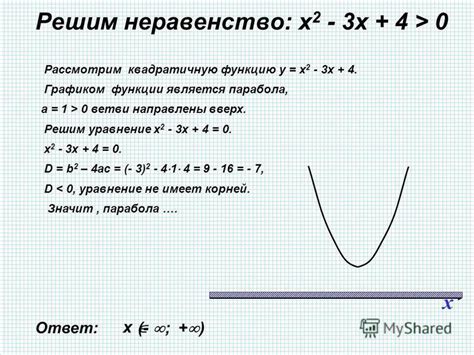
Квадратичные функции имеют некоторые характерные свойства, которые позволяют легко их определить:

1. Парабола: График квадратичной функции представляет собой параболу – кривую, имеющую форму параболической чаши с ветвями, направленными вверх или вниз. Форма параболы и направление ее ветвей определяются знаком коэффициента a. Если a > 0, парабола направлена вверх, а если a
2. Вершина: У параболы, задаваемой квадратичной функцией, всегда есть вершина – точка, где парабола достигает своего минимума или максимума. Координаты вершины можно вычислить по формулам:

x₀ = -b / (2a),

y₀ = f(x₀) = f(-b / (2a)).

3. Ось симметрии: Ось симметрии параболы задается уравнением x = -b / (2a). Она пересекает параболу в вершине и является осью симметрии, разделяющей параболу на две одинаковые половины.
4. Нули: Нулями квадратичной функции называются значения x, при которых f(x) = 0. Нули можно найти, решив уравнение ax^2 + bx + c = 0.

Зная характеристики квадратичной функции, можно легко построить ее график, определить форму параболы и ее вершину, а также найти ее ось симметрии и нули.

Как построить график квадратичной функции

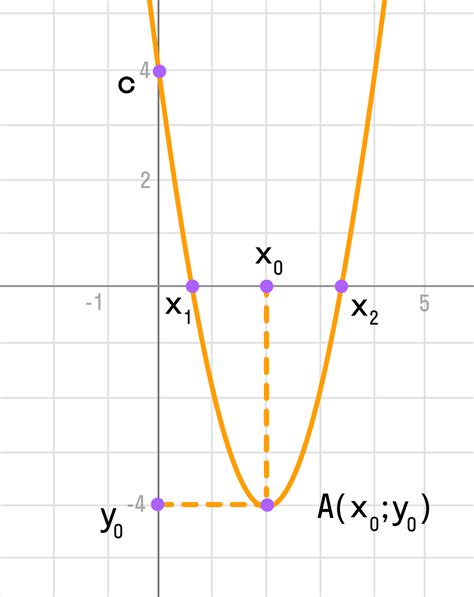
Чтобы построить график квадратичной функции, следуйте следующим шагам:

1. Определите форму функции. Для этого проверьте коэффициент при квадрате переменной. Если коэффициент положительный, парабола направлена вверх, если отрицательный - вниз.
2. Найдите вершину параболы. Для этого используйте формулу x = -b / (2a), где a и b - коэффициенты при x^2 и x соответственно. Вершина параболы имеет координаты (x, y), где x - координата вершины, а y - значение функции в вершине.
3. Найдите дополнительные точки на графике. Для этого выберите несколько значений переменной x, подставьте их в функцию и найдите соответствующие значения y.
4. Проведите график через полученные точки. Помимо вершины, выберите несколько других точек и отметьте их на графике. Затем соедините полученные точки плавной кривой, чтобы получить параболу.

Важно помнить, что более подробное и точное построение графика возможно с использованием компьютерных программ или калькуляторов, которые могут автоматически рассчитывать значения функции и строить график.

Построение графика квадратичной функции позволяет визуализировать ее особенности и анализировать различные аспекты ее поведения. Это инструмент, который помогает лучше понять и изучить квадратичные функции и их свойства.

Как снять счет на видео при построении квадратичной функции и ее графика

Построение квадратичной функции и ее графика может быть сложной задачей, но если вы хотите сделать видеоурок или презентацию о данной теме, можно использовать специальные инструменты и методы, чтобы снять счет в процессе.

Первым шагом является выбор программы для построения графиков, которая позволяет записывать видео экрана. Существует множество таких программ, включая Camtasia, OBS Studio, Apowersoft и другие. Выберите наиболее удобную и понятную для вас.

Затем следует подготовить данные для построения графика квадратичной функции. Рекомендуется использовать таблицу со значениями x и соответствующими им значениями f(x). Можно вычислить эти значения самостоятельно или использовать специальные калькуляторы для квадратичных функций.

После этого можно построить сам график, используя выбранную программу. Обычно это делается путем указания точек на координатной плоскости, через которые будет проходить график. Не забудьте подписать оси координат и указать масштаб.

Теперь самое интересное - снятие счета на видео. В программе для записи экрана выберите соответствующую функцию и начните съемку. В процессе построения графика квадратичной функции рассказывайте о каждом шаге, объясняйте, какие точки вы выбираете и почему.

Кроме того, можно использовать курсор для выделения точек и линий на графике, чтобы сделать процесс более понятным и наглядным для зрителей. Рассказывайте о важных особенностях графика, таких как вершина параболы, направление ветвей и симметрия.

Важно помнить о правилах композиции видеоурока или презентации: говорить четко и громко, привлекать внимание зрителя, использовать хорошее освещение и качественное звуковое оборудование.

По окончании съемки видео, просмотрите его для выявления ошибок или неточностей. Если все хорошо, вы можете сохранить видео и поделиться им с другими людьми.

Построение квадратичной функции и ее графика в видеоформате с счетом поможет вашим зрителям лучше понять и запомнить данный материал. Не забудьте дать возможность задавать вопросы и оставлять комментарии под видео, чтобы выяснить все дополнительные нюансы темы.

Как использовать видео для обучения построению квадратичных функций и графиков

Изучение построения квадратичных функций и графиков может быть сложной и абстрактной задачей для многих студентов. Однако использование видео материала в обучении может помочь учащимся лучше понять эту тему и научиться строить квадратичные функции и графики.

Видео обучение позволяет студентам наглядно видеть каждый этап построения квадратичной функции и графика. Использование видео может помочь студентам лучше понять концепцию квадратичных функций, таких как вершина, ось симметрии и направление открытия.

Видео материалы также могут предоставить студентам возможность учиться на конкретных примерах. Учащиеся могут видеть, как коэффициенты влияют на форму графика квадратичной функции. Это может помочь им лучше понять, как изменение значений коэффициентов изменяет форму графика.

Видео также может быть полезным для визуализации процесса решения задач, связанных с графиками квадратичных функций. Ученики могут видеть, как строить графики по заданным уравнениям или как находить значения вершины и оси симметрии. Видео материалы могут быть удобными для повторения и закрепления изучаемого материала.

Использование видео для обучения построению квадратичных функций и графиков может быть удобным и эффективным инструментом. С его помощью, учащиеся могут улучшить понимание концепций квадратичных функций и научиться лучше визуализировать их на графиках.