Меридиана - это прямая линия, которая проходит через вершину третьего угла треугольника и делит противоположную сторону пополам. Меридиана является важным инструментом в геометрии и может быть построена с помощью циркуля.
Для построения меридианы необходимо использовать следующие шаги:
- Возьмите циркуль и отметьте на сторонах треугольника равные расстояния от вершины третьего угла.
- Проведите дугу с одной стороны треугольника и пересеките другую сторону.
- Повторите этот шаг с другой стороной треугольника.
- Точка пересечения обоих дуг является вершиной меридианы.
- Проведите прямую через эту точку и вершину третьего угла, чтобы создать меридиану.
Построение меридианы в треугольнике с помощью циркуля - это основной метод, который используется для решения различных задач в геометрии. Изучение и применение этого метода поможет вам лучше понять структуру треугольника и его свойства.
Построение меридианы треугольником циркулем
Для построения меридианы треугольником с помощью циркуля необходимо выполнить следующие шаги:
- Возьмите циркуль и поставьте его одну ножку в вершине треугольника, а другую ножку на противоположной стороне треугольника.
- Сделайте маленький развод циркулем и проведите окружность.
- Сделайте то же самое, поставив циркуль одну ножку в другой вершине треугольника, а другую ножку на противоположной стороне треугольника.
- Сделайте развод циркулем и проведите окружность.
- Найдите точку пересечения этих двух окружностей. Эта точка будет серединой противоположной стороны треугольника.
- Соедините вершину треугольника со свеже найденной серединой прямой. Это и будет меридиана треугольника.
Построив меридиану треугольника, вы сможете использовать ее для решения задач на поиск центра окружности, описанной вокруг треугольника, а также для доказательства различных свойств и теорем в геометрии.
Необходимо помнить, что для построения точной меридианы треугольником циркулем, необходимо быть аккуратным и точным при работе с инструментами.
Определение треугольника и меридианы
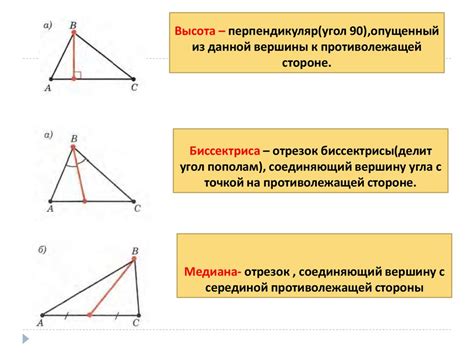
Меридиана - это прямая, которая соединяет середину одной стороны треугольника с противоположным углом. Меридиана, также известная как медиана, делит сторону треугольника пополам и пересекает точку пересечения меридиан другой стороны треугольника. Треугольник имеет три меридианы, которые пересекаются в одной общей точке, называемой центром меридиан.
Например, для треугольника ABC:
- Меридиана AC - это прямая, которая соединяет точку D, середину стороны BC, с противоположным углом A.
- Меридиана AB - это прямая, которая соединяет точку E, середину стороны AC, с противоположным углом B.
- Меридиана BC - это прямая, которая соединяет точку F, середину стороны AB, с противоположным углом C.
Построение меридианы в треугольнике с помощью циркуля позволяет определить его центр меридиан и является важным шагом при решении геометрических задач, связанных с треугольниками.
Что такое меридиана в треугольнике

Меридианы могут быть построены внутри треугольника, если соединить каждую из вершин с серединой противоположной стороны. Полученные линии называются внутренними меридианами. Также возможно построить внешние меридианы - отрезки, которые соединяют вершины треугольника с серединами продолжений противоположных сторон.
Меридианы имеют некоторые интересные свойства. Внутренние меридианы пересекаются в одной точке, которая называется центром медиан. Данная точка делит каждый из внутренних меридиан на отрезки, пропорциональные длинам смежных сторон треугольника. Внешние меридианы также пересекаются в одной точке, которая называется центром внешней меридианной.
Меридианы широко используются в геометрии треугольника при решении различных задач. Они помогают найти и изучить различные свойства треугольника, а также строить новые линии и точки, связанные с треугольником.
| Вид меридиана | Описание |
|---|---|
| Внутренняя меридиана | Отрезок, соединяющий вершину треугольника с серединой противоположной стороны внутри треугольника. |
| Внешняя меридиана | Отрезок, соединяющий вершину треугольника с серединой продолжения противоположной стороны вне треугольника. |
| Центр меридиан | Точка, в которой пересекаются все внутренние меридианы или все внешние меридианы. |
Доказательство существования меридианы

Предположим, у нас есть треугольник ABC. Пусть D – середина стороны AC треугольника. Требуется построить меридиану из вершины B.
Возьмем циркуль и установим его в точке D радиусом, большим половины стороны BC. Опишем окружность, которая проходит через точки B и C.
Найдем точку пересечения луча, исходящего из вершины B, и полученной окружности. Обозначим эту точку как E.
Докажем, что точка E также является серединой стороны AB. Рассмотрим стороны треугольника ABC: AB, BC и AC. Так как D – середина стороны AC, то отрезок BD делит сторону AC на две равные части.
Также, так как точка E находится на окружности, описанной вокруг треугольника ABC, то отрезки BE и CE равны между собой.
Аналогично, так как точка D находится на окружности с радиусом, равным половине стороны BC, отрезок BD также делит сторону BC на две равные части.
Таким образом, мы видим, что отрезок BE делит сторону AC на две равные части, и отрезок BD делит сторону BC на две равные части. Следовательно, точка E является серединой стороны AB.
Таким образом, мы доказали, что меридиана всегда существует в треугольнике. Этот факт можно использовать при построении и исследовании треугольников с использованием циркуля.
Как построить меридиану с помощью циркуля
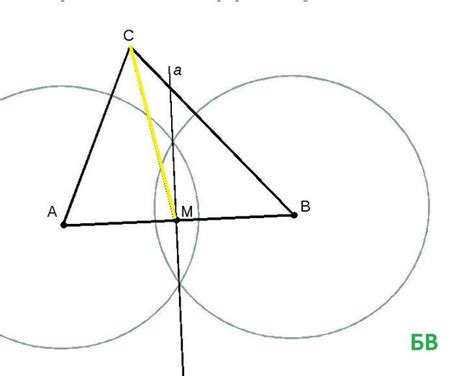
- Возьмите циркуль и установите его одной ножкой на вершину треугольника.
- Расставьте другую ножку циркуля на противоположной стороне треугольника так, чтобы она проходила через точку на стороне, находящейся на равном расстоянии от основания треугольника.
- Сделайте резкий поворот циркуля вокруг первой ножки, чтобы нарисовать дугу на стороне треугольника.
- Повторите шаги 2-3 для другой стороны треугольника, чтобы нарисовать вторую дугу.
- Точка пересечения дуг представляет собой вершину меридианы.
- Соедините вершину меридианы с точками на противоположных сторонах треугольника, чтобы нарисовать меридиану.
Теперь у вас есть готовая меридиана, которая делит треугольник пополам! Этот метод позволяет с легкостью построить меридиану с помощью циркуля и является одним из способов решения геометрических задач.
Шаги построения меридианы треугольника
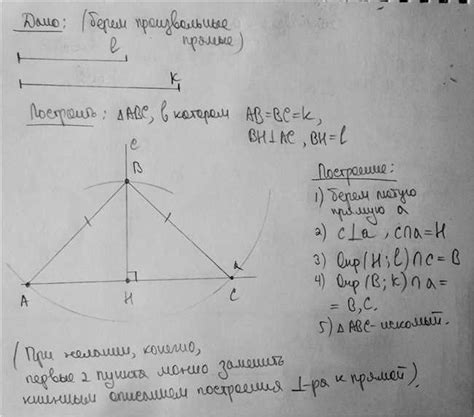
Построение меридианы треугольника с помощью циркуля включает в себя несколько шагов:
- Возьмите циркуль и откройте его на расстояние, большее любой из сторон треугольника.
- Установите одно из ног циркуля на одном из вершин треугольника и проведите дугу, которая пересечет другие две стороны треугольника.
- Оставив расстояние на циркуле неизменным, установите другую ногу на одной из оставшихся вершин треугольника и снова проведите дугу, которая пересечет третью сторону.
- Точка пересечения двух построенных дуг является вершиной меридианы треугольника.
- Соедините вершину меридианы с вершинами треугольника.
Таким образом, используя циркуль, можно построить меридиану треугольника, которая является линией, соединяющей вершины треугольника и проходящей через точку пересечения медиан треугольника.
Первый шаг построения меридианы
Для построения меридианы в треугольнике с помощью циркуля, необходимо выполнить следующие действия:
- Возьмите циркуль и расставьте его концы на двух сторонах треугольника.
- Установите размер циркуля таким образом, чтобы его один конец соприкасался с вершиной треугольника.
- Сделайте отметку на стороне треугольника в месте соприкосновения циркуля с этой стороной.
- Повторите эти действия для двух других сторон треугольника.
Таким образом, вы получите три точки на сторонах треугольника, через которые проходит будущая меридиана. Они служат отправной точкой для дальнейшего построения меридианы с помощью циркуля. Переходите ко второму шагу построения!
Второй шаг построения меридианы

После того, как мы провели первую часть меридианы, необходимо перейти ко второму шагу. Для этого мы возьмем циркуль и установим его одну из ног на одну из вершин треугольника, а другую ногу расширим до пересечения с противоположной стороной треугольника. Затем мы проведем дугу окружности.
Чтобы выполнить этот шаг правильно, необходимо убедиться, что центр окружности находится на середине выбранной противоположной стороны треугольника. Для этого мы достаточно расчертить две дуги окружностей с радиусами, равными половине длины выбранной стороны треугольника, и провести пересечение этих дуг. Точка пересечения будет являться центром окружности.
После того, как мы определили центр окружности, мы проведем саму окружность, используя циркуль. Чтобы получить меридиану, необходимо провести линию от вершины треугольника, где мы начали построение, до пересечения окружности с противоположной стороной треугольника. Таким образом, мы получим меридиану, разделяющую треугольник на две равные части.
Третий шаг построения меридианы

После выполнения первых двух шагов построения меридианы в треугольнике, переходим к третьему шагу. На данном этапе мы будем проводить отметку на одной из боковых сторон треугольника.
Для того чтобы провести отметку, необходимо взять циркуль с заданной длиной радиуса и установить одну его ножку в точку пересечения биссектрисы угла, а другую ножку разместить на противоположной стороне треугольника, на продолжении стороны изначальной к точке пересечения биссектрис. Затем провести дугу внутри треугольника, пересекающую третью сторону треугольника.
Новая точка пересечения дуги и третьей стороны будет служить отметкой для проведения меридианы. Проводим линию, проходящую через точку пересечения биссектрисы и новую точку пересечения дуги с третьей стороной. Получившаяся линия и будет меридианой в треугольнике.
Таким образом, выполнив третий шаг построения меридианы, мы получим еще одну важную линию в треугольнике, которая определит взаимное расположение вершин и углов этой геометрической фигуры.
Четвертый шаг построения меридианы

После выполнения предыдущих трех шагов построения меридианы в треугольнике, перейдем к реализации четвертого шага.
Четвертый шаг заключается в построении точки пересечения основ треугольника с линиями, проведенными из вершин до середин противолежащих сторон.
Для этого, возьмите циркуль и откройте его на расстояние, равное половине одной из сторон треугольника. Поставьте концы циркуля на середины двух противолежащих сторон, а потом проведите дуги, пересекающиеся в точке, находящейся внутри треугольника.
Получившаяся точка будет точкой пересечения всех трех линий, если вы правильно выполнили предыдущие шаги. Эта точка является серединой меридианы треугольника.
Определение меридианы треугольника – это проведение линии, проходящей через вершину треугольника и середину противолежащей стороны. Меридиана разделяет треугольник на две равные части.
На этом завершается четвертый шаг построения меридианы треугольника с помощью циркуля.
Не забудьте проделать все четыре шага для каждого треугольника, если вам необходимо построить меридиану в нескольких треугольниках.