Геометрия и алгебра - две науки, которые тесно взаимосвязаны друг с другом. В геометрии мы изучаем пространственные фигуры и их свойства, в то время как в алгебре мы работаем с числами и алгебраическими выражениями. Но что происходит, когда эти две науки соединяются? Возникают интересные задачи, одной из которых является построение отрезка с Корнем из 3 разделенный на 2. В этом гиде я расскажу, как решить эту задачу как с помощью геометрических методов, так и с использованием алгебры.
Для начала разберемся, что такое отрезок с Корнем из 3 разделенный на 2. Это отрезок, который имеет определенное соотношение длин его частей. Обозначим длину всего отрезка за x. Тогда одна его часть будет иметь длину x/2, а вторая x - x/2 = x/2. Мы знаем, что отношение длин частей должно быть равно корню из 3, то есть (x/2) / (x/2) = √3. Из этого уравнения можно найти значение x и построить такой отрезок.
Теперь рассмотрим, как построить такой отрезок с помощью геометрических методов. Нарисуем прямую и отметим на ней две точки A и B. Расстояние между ними должно быть равно длине отрезка x. Затем, из точки A проведем перпендикуляр к прямой и обозначим точку пересечения с прямой за C. Тогда отрезок AC будет иметь длину x/2, а отрезок BC - x/2. Таким образом, получаем отрезок с Корнем из 3 разделенный на 2. Этот метод можно использовать для решения задачи на практике.
В итоге, построение отрезка с Корнем из 3 разделенный на 2 - это интересная задача, которая требует использования знаний и геометрии, и алгебры. Но с помощью правильных методов и формул, ее можно успешно решить. Используйте этот гид, чтобы справиться с этой задачей и узнать больше о геометрии и алгебре.
Построение отрезка с корнем из 3 в геометрии
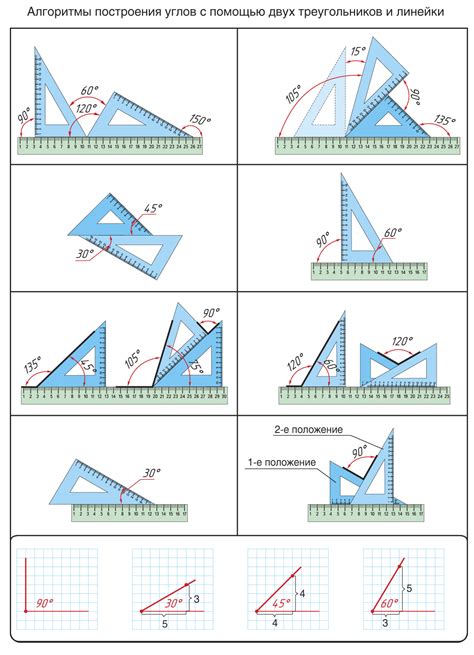
Построение отрезка с корнем из 3 в геометрии может показаться сложной задачей, однако существует простой способ решения данной задачи. Для начала, необходимо определиться с масштабом построения и решить, какую длину отрезка с корнем из 3 мы хотим построить.
Для построения отрезка с корнем из 3, мы будем использовать соотношение сторон треугольника, известное как "теорема Пифагора". Согласно этой теореме, квадрат гипотенузы (самой длинной стороны треугольника) равен сумме квадратов катетов (двух других сторон).
Итак, пусть длина гипотенузы (отрезка, который мы хотим построить) будет равна х. Тогда, длина одного из катетов будет равна корню из 3, а второго катета - 1.
Далее, мы можем записать уравнение по теореме Пифагора:
| Строительный шаг | Выражение | Результат |
|---|---|---|
| 1 | x^2 = (√3)^2 + 1^2 | x^2 = 3 + 1 |
| 2 | x^2 = 4 | x = √4 |
Таким образом, получаем, что длина отрезка с корнем из 3 равна 2. Мы успешно построили отрезок с корнем из 3, используя геометрический подход и теорему Пифагора.
Геометрическое построение отрезка с корнем из 3
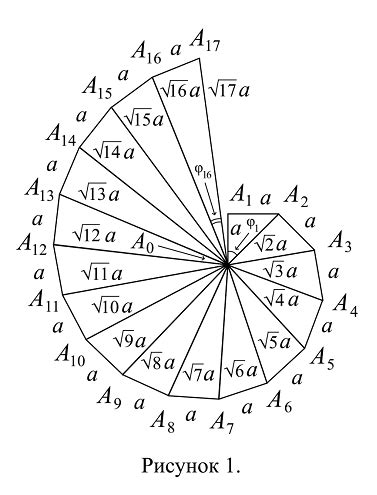
Для построения отрезка с корнем из 3 необходимо выполнить следующие шаги:
- Возьмите любую точку на плоскости и назовите ее начальной точкой.
- С помощью линейки нанесите прямую, проходящую через начальную точку, образующую угол в 60 градусов с осью абсцисс.
- На этой прямой отложите отрезок длиной, равной 2 единицам.
- Продолжив прямую, отложите от точки начала отрезка длиной 1 единицу.
- Соедините последнюю точку данной прямой с начальной точкой, получив отрезок с корнем из 3.
Данный метод позволяет геометрически построить отрезок с корнем из 3 с использованием простых инструментов и без использования технических вычислений.