Перпендикуляр – это прямая, которая пересекает другую прямую и создает прямой угол. Построение перпендикуляра является важной задачей в геометрии, так как оно позволяет определить точку или отрезок, находящийся под прямым углом к другому объекту. В данной статье мы рассмотрим один из способов построения перпендикуляра с использованием серединного циркуля и линейки.

Первым шагом в построении перпендикуляра является рисование прямой, на которой нам нужно построить перпендикуляр. Затем мы отмечаем на этой прямой две точки, которые отстоят от начала и конца прямой на одинаковое расстояние. Эти точки будут служить нам в качестве центра для построения окружностей серединного циркуля.

Далее мы берем линейку и прокладываем ее через эти две точки. Посредством линейки мы отмечаем две точки на прямой. По оси симметрии этих двух точек мы рисуем перпендикуляр с помощью серединного циркуля. Получившийся перпендикуляр будет пересекать исходную прямую под прямым углом и является искомым результатом.

Перпендикуляр

Для построения перпендикуляра сначала необходимо провести прямую линию, которую мы будем перпендикулярно пересекать. Затем мы берем серединный циркуль и ставим его в произвольной точке на этой линии.

Затем мы делаем два равных отрезка на линии с помощью циркуля и линейки. Затем, не меняя расстояние циркуля и линейки, мы переносим эти отрезки на другую сторону линии. Получившиеся точки будут точками пересечения прямой с перпендикулярной линией.

Подводя итог, построение перпендикуляра с использованием серединного циркуля и линейки несложно. Зная основные шаги и правила, вы сможете выполнять такие построения самостоятельно.

Серединный циркуль

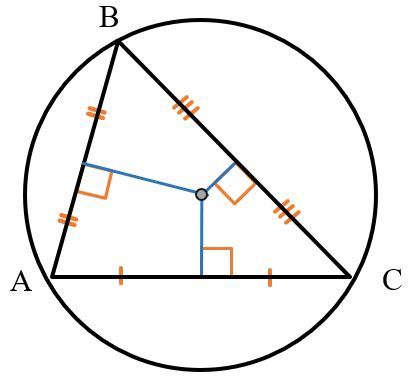
Для построения перпендикуляра с помощью серединного циркуля нужно следовать следующим шагам:

1. На отрезке AB, проведенном линейкой, найдите его середину точку M.
2. Установите серединный циркуль на точку M и сделайте отметку на линейке в одном из направлений.
3. Сделайте две окружности с центром в точке M, используя разные радиусы циркуля. Одна окружность должна пересекать линейку в точке A, а вторая - в точке B.
4. Соедините точки пересечения окружностей с линейкой. Полученный отрезок будет перпендикулярным к отрезку AB.

Используя серединный циркуль, можно легко строить перпендикуляры и выполнять другие геометрические построения, связанные с серединами отрезков.

Серединный циркуль является удобным и надежным инструментом, который позволяет точно строить перпендикулярные отрезки. Он широко применяется в геометрических построениях и может использоваться как начинающими, так и опытными учениками.

Линейка

Основное назначение линейки – измерение и прямолинейное построение отрезков. Для этого необходимо расположить линейку на плоскости так, чтобы ее начало совпадало с началом отрезка, а основание линейки пересекало конечную точку отрезка. Затем нужно прочитать значение измерения на градуировке линейки.

Линейка также может использоваться для проведения параллельных отрезков. Для этого необходимо установить линейку так, чтобы она была параллельна нужной прямой линии. Затем можно повернуть линейку вокруг своей оси и провести параллельный отрезок.

Для более точных измерений и построений необходимо использовать линейку с мелкими делениями и делениями большей точности. Также существуют специальные линейки с дополнительными функциями, например, с отверстиями для проведения круговых или дуговых отрезков.

Линейка является одним из основных инструментов для строительства перпендикуляров серединных. С ее помощью можно провести равные отрезки и построить перпендикулярную линию, которая будет проходить через середину отрезка.

Построение перпендикуляра

1. Задайте точку А на плоскости. Это будет одна из точек перпендикуляра.
2. Возьмите линейку и проведите от точки А отрезок AB любой длины.
3. Откройте серединный циркуль на расстояние, превышающее половину длины отрезка AB.
4. Установите острие циркуля в точку B и проведите две дуги, пересекающие отрезок AB по разные стороны, обозначив точки C и D.
5. Соедините точки C и D линейкой. Полученная прямая перпендикулярна отрезку AB и проходит через его середину.

Теперь вы знаете, как построить перпендикуляр серединный циркулем и линейкой! Этот метод является простым и эффективным способом решения данной задачи в геометрии.

Построение серединного циркуля

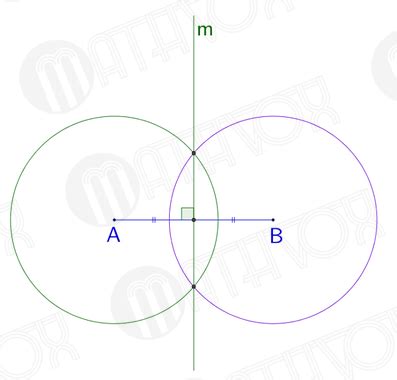
Для построения серединного циркуля нам понадобится циркуль и линейка.

1. Выберите на плоскости две точки, через которые должна проходить требуемая прямая.
2. С помощью линейки соедините выбранные точки прямой.
3. Установите концы линейки на плоскость таким образом, чтобы они находились по разные стороны от прямой.
4. Зажмите циркуль так, чтобы его стержень совпал с одной из точек прямой, а его ножка касалась ее второй точки.
5. Если середина прямой должна быть по отношению к первой точке, то отведите с помощью циркуля от первой точки любую отрезки на половину длины прямой.
6. Соедините концы отрезков прямой с помощью линейки.
7. Точка пересечения получившейся линии и прямой является серединой прямой.
8. Вы можете проверить правильность построенной серединной точки, измерив расстояние от нее до обоих концов прямой, оно должно быть равным.

Теперь вы знаете, как построить серединный циркуль с использованием циркуля и линейки. Этот метод основывается на применении геометрических конструкций и может быть использован в различных задачах, связанных с визуальным представлением прямой. Практикуйтесь и у вас получится!

Построение перпендикуляра с использованием линейки

Для начала выберем точку на прямой, через которую хотим провести перпендикуляр. Поставим линейку наши выбранные точку и перпендикулярно ей прямо и сместим линейку так, чтобы один конец линейки оказался на выбранной точке, а другой конец - за пределами прямой.

Теперь, не снимая палец с линейки, поворачиваем ее на 90 градусов и проводим линию с помощью карандаша. Эта линия будет перпендикулярной к исходной прямой и проходить через выбранную точку.

Таким образом, используя только линейку, можно легко построить перпендикуляр к выбранной прямой через выбранную точку. Этот способ прост и эффективен, и может использоваться в различных геометрических задачах.

Примеры построения перпендикуляра и серединного циркуля

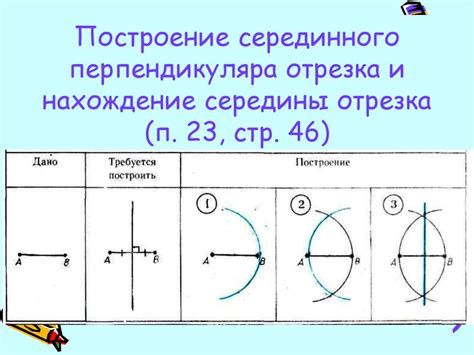
Ниже приведены примеры построения перпендикуляра и серединного циркуля с помощью циркуля и линейки:

1. Построение перпендикуляра:

• Пусть дана прямая AB.
• Выберем точку O вне прямой AB.
• С помощью циркуля построим окружность с центром в точке O и проходящую через точки A и B.
• Обозначим точки пересечения окружности с прямой AB как C и D.
• Соединим точки C и D.
• Линия, проходящая через точку O и перпендикулярная прямой AB, будет линией, проходящей через точки C и D.

• Пусть дан сегмент прямой AB.
• С помощью линейки найдем середину отрезка AB и обозначим ее как точку M.
• С помощью циркуля поставим радиус, равный половине длины отрезка AB, из точки M.
• Нарисуем окружность с центром в точке M и радиусом, который мы только что поставили.

Вот и все! Теперь вы знаете, как построить перпендикуляр и серединный циркуль с помощью циркуля и линейки.