Как построить прямую через заданные точки в MATLAB — подробная инструкция с шагами и примерами кода

На чтение 9 мин Опубликовано 14.11.2024 Обновлено 14.11.2024

Построение прямой через заданные точки - одна из базовых задач в математическом моделировании и анализе данных. В среде MATLAB это можно сделать с помощью нескольких простых команд. В этой статье мы рассмотрим примеры и покажем, как построить прямую через заданные точки с использованием различных методов в MATLAB.

Один из самых простых способов построить прямую через заданные точки - это использовать функцию plot. Для начала, нам нужно задать координаты точек, через которые должна проходить прямая. Например, пусть у нас есть две точки A(1, 2) и B(3, 4). Тогда код для построения прямой через эти точки будет выглядеть следующим образом:

x = [1, 3];

y = [2, 4];

plot(x, y);

После выполнения этих команд на графике появится прямая, проходящая через точки A и B. Это самый простой способ решения задачи, но в MATLAB есть и другие, более сложные методы для более точного построения прямой.

Описание задачи

В задаче требуется построить прямую через две заданные точки на плоскости с использованием языка программирования MATLAB. Для этого необходимо найти уравнение прямой, которая проходит через заданные точки.

Входные данные: координаты двух точек на плоскости (x1, y1) и (x2, y2).

Выходные данные: уравнение прямой в виде y = mx + c, где m - наклон прямой, c - свободный коэффициент.

Для решения задачи можно воспользоваться формулой для нахождения уравнения прямой через две точки:

Рассчитать значение наклона m с использованием формулы: m = (y2 - y1) / (x2 - x1).
Рассчитать значение свободного коэффициента c с использованием формулы: c = y1 - m * x1.

После нахождения значений m и c, можно записать уравнение прямой в виде y = mx + c и построить ее с помощью графической функции в MATLAB.

MATLAB как инструмент для решения задачи

Использование MATLAB для построения прямой через заданные точки облегчает процесс анализа данных и позволяет визуально представить результаты. Для этого можно использовать функцию plot, которая позволяет строить графики различных типов.

Для построения прямой через заданные точки в MATLAB необходимо задать координаты этих точек с помощью векторов. Затем можно использовать функцию plot, указав векторы с координатами X и Y точек.

Пример кода для построения прямой через две точки (-1, 2) и (3, 4) в MATLAB:


x = [-1, 3];
y = [2, 4];
plot(x, y, '-o');

В результате выполнения этого кода будет построена прямая, проходящая через указанные точки и представленная графически. Знак "-o" указывает на стиль линии и маркеры точек.

Более сложные задачи, например, построение прямой через несколько точек или решение систем уравнений, также могут быть реализованы с помощью MATLAB. Библиотека MathWorks предоставляет множество функций и инструментов, которые могут быть использованы для выполнения различных операций и анализа данных.

Пример кода	Описание
`polyfit`	Функция для нахождения коэффициентов полинома, который наилучшим образом приближает заданные точки.
`lsqcurvefit`	Функция для нахождения наилучшего соответствия модели заданным данным с использованием метода наименьших квадратов.
`fmincon`	Функция для решения задачи условной оптимизации с ограничениями.

Таким образом, использование MATLAB для решения задачи построения прямой через заданные точки обеспечивает простоту и эффективность в анализе данных.

Описание математической модели прямой

Коэффициент наклона m показывает, насколько быстро растет или уменьшается значение координаты y в зависимости от изменения значения координаты x. Положительное значение m означает, что прямая стремится к увеличению значения координаты y при увеличении значения координаты x, а отрицательное значение m означает уменьшение значения координаты y.

Значение c обозначает точку пересечения прямой с осью ординат (y-осью). Если c положительное, то прямая пересекает ось ординат выше начала координат, а если c отрицательное, то ниже начала координат.

Таким образом, математическая модель прямой позволяет нам определить положение прямой в пространстве и предсказывать значения координат y для различных значений координаты x на этой прямой.

Уравнение прямой в декартовой системе координат

Для построения прямой через заданные точки в MATLAB можно воспользоваться различными методами, включая использование функций polyfit, polyval и plot. Пример решения задачи построения прямой через две заданные точки:

Определить координаты заданных точек: (x1, y1) и (x2, y2).
Вычислить угловой коэффициент прямой m по формуле: m = (y2 - y1) / (x2 - x1).
Вычислить свободный член прямой b по формуле: b = y1 - m * x1.
Создать массив x, содержащий значения x-координат, включая начальную и конечную точки прямой.
Вычислить значения y-координат прямой по формуле: y = mx + b, используя функцию polyval.
Построить график прямой, используя функцию plot.

Пример кода в MATLAB:

x1 = 0;
y1 = 1;
x2 = 5;
y2 = 2;
m = (y2 - y1) / (x2 - x1);
b = y1 - m * x1;
x = linspace(x1, x2);
y = polyval([m, b], x);
plot(x, y);
hold on;
plot(x1, y1, 'ro');
plot(x2, y2, 'ro');
title('Прямая через заданные точки');
xlabel('x');
ylabel('y');
legend('Прямая', 'Точки');
hold off;

В этом примере заданы две точки с координатами (0, 1) и (5, 2). Программа вычисляет угловой коэффициент прямой и свободный член, а затем строит график прямой, проходящей через эти точки. График также содержит отмеченные точки для наглядности.

Использование функций polyfit, polyval и plot позволяет удобно и эффективно строить прямую через заданные точки в декартовой системе координат в MATLAB.

Расчет коэффициентов уравнения прямой

Для построения прямой через заданные точки необходимо расчитать коэффициенты уравнения прямой. Уравнение прямой в общем виде имеет следующий вид:

y = mx + b

где m - коэффициент наклона прямой (slope), а b - свободный член (intercept).

Для расчета коэффициентов можно воспользоваться формулами:

m = (y2 - y1) / (x2 - x1)

b = y1 - m * x1

где (x1, y1) и (x2, y2) - координаты заданных точек на плоскости.

Таким образом, зная координаты точек, мы можем вычислить значения коэффициентов m и b и использовать их для построения прямой через эти точки.

Варианты построения прямой в MATLAB

В MATLAB существует несколько способов построения прямой через заданные точки. Рассмотрим некоторые из них:

Использование функции plot. Этот способ наиболее простой и используется, когда нас интересует только визуализация прямой. Мы можем передать в функцию plot координаты двух точек и получить прямую, проходящую через них. Например:

x = [1, 2];
y = [3, 4];
plot(x, y);

Этот код построит отрезок, соединяющий точки (1, 3) и (2, 4).

Использование метода наименьших квадратов для вычисления коэффициентов прямой. Этот способ подходит, когда нам необходимо получить уравнение прямой или использовать коэффициенты в дальнейших вычислениях. Для этого мы можем использовать функцию polyfit. Пример использования:

x = [1, 2];
y = [3, 4];
coefficients = polyfit(x, y, 1);
a = coefficients(1);
b = coefficients(2);

В результате выполнения этого кода мы получим уравнение прямой вида y = ax + b, где a и b - коэффициенты, которые мы можем использовать для нахождения значений y для любых заданных значений x.

Использование функции lsline. Этот способ удобен, когда нам необходимо визуализировать прямую, построенную методом наименьших квадратов. Мы можем использовать функцию lsline сразу после построения графика точек. Например:

x = [1, 2];
y = [3, 4];
plot(x, y);
lsline;

Этот код построит график точек и прямую, построенную методом наименьших квадратов.

Таким образом, в MATLAB есть несколько вариантов построения прямой через заданные точки. Выбор конкретного способа зависит от задачи, которую необходимо решить.

Использование функции plot

Функция plot в MATLAB позволяет строить графики простыми способами. Она принимает в качестве аргументов массивы координат точек и параметры для настройки внешнего вида графика.

Для построения прямой через заданные точки с помощью функции plot необходимо задать массивы с координатами точек по оси x и y. После этого можно вызвать функцию plot с этими массивами в качестве параметров:

x = [1, 2, 3, 4];
y = [1, 3, 2, 4];
plot(x, y);

Этот код построит прямую, проходящую через точки (1, 1), (2, 3), (3, 2) и (4, 4).

Чтобы настроить внешний вид графика, можно передать дополнительные параметры в функцию plot. Например, можно изменить цвет и стиль линии, добавить маркеры на точках, добавить заголовок и подписи к осям:

x = [1, 2, 3, 4];
y = [1, 3, 2, 4];
plot(x, y, 'r--o');
title('График прямой');
xlabel('Ось x');
ylabel('Ось y');

В этом примере линия будет красного цвета, иметь пунктирный стиль и маркеры в виде точек. Также будет добавлен заголовок и подписи к осям.

Функция plot позволяет строить не только прямые, но и различные другие графики, включая кривые, столбчатые диаграммы и диаграммы рассеяния.

Использование функции line

В MATLAB существует специальная функция называемая line, которая позволяет построить прямую через заданные точки. Эта функция может быть полезна, если необходимо визуально представить прямую на графике или визуально подтвердить правильность вычислений.

Для использования функции line необходимо передать ей координаты двух точек, через которые должна проходить прямая. Например:

x = [1, 3];
y = [4, 8];
line(x, y);

В этом примере будет построена прямая, проходящая через точки (1, 4) и (3, 8).

Функция line также может принимать необязательные параметры, такие как цвет и стиль линии.

Например, можно изменить цвет линии на красный и задать ей пунктирный стиль:

line(x, y, 'color', 'r', 'linestyle', '--');

Это создаст пунктирную красную линию, проходящую через точки (1, 4) и (3, 8).

Использование функции line может быть полезным при визуализации данных и анализе результатов численных расчетов.

Построение прямой через две заданные точки

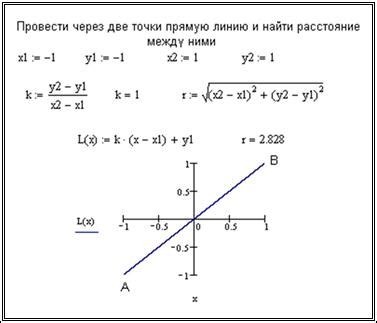
Для начала, задайте координаты двух точек, через которые должна проходить прямая. Например, пусть первая точка имеет координаты (x1, y1), а вторая точка - (x2, y2).

Далее, используйте функцию plot с аргументами в виде массивов координат x и y для заданных точек:

x = [x1, x2];
y = [y1, y2];
plot(x, y);

Выполнение этих команд приведет к построению прямой, проходящей через две заданные точки.

Например, если мы хотим построить прямую, проходящую через точки (1, 2) и (3, 4), код будет выглядеть следующим образом:

x = [1, 3];
y = [2, 4];
plot(x, y);

После выполнения этих команд на графике будет построена прямая, проходящая через указанные точки.

Описание алгоритма

Построение прямой через заданные точки в MATLAB может быть выполнено с помощью алгоритма на основе метода наименьших квадратов. Ключевая идея алгоритма заключается в том, чтобы найти уравнение прямой, близкое к оптимальному решению, минимизируя сумму квадратов расстояний между каждой точкой и прямой.

Шаги алгоритма:

Получить координаты заданных точек.
Вычислить средние значения координат по оси X и по оси Y.
Вычислить отклонения координат каждой точки от средних значений.
Вычислить суммы произведений отклонений по осям X и Y.
Вычислить суммы квадратов отклонений по осям X и Y.
Вычислить наклон прямой, используя формулу: slope = (сумма произведений отклонений по осям X и Y) / (сумма квадратов отклонений по оси X).
Вычислить точку пересечения прямой с осью Y, используя формулу: y_intercept = среднее значение координаты Y - slope * среднее значение координаты X.
Построить уравнение прямой вида: y = slope * x + y_intercept, где x - координата точки, y - значение прямой для соответствующей координаты x.

Полученное уравнение прямой использовать для построения графика в MATLAB.