Прямые и параллельные линии - основные геометрические фигуры, которые широко применяются в различных отраслях науки и техники. Знание и умение строить эти линии является одним из основных навыков геометрии.

Прямая линия - это линия, у которой все точки лежат на одной и той же прямой. Она имеет нулевую ширину и нулевую толщину.

Свойства прямой линии включаются в двух основных конструкциях: задание через две точки и задание через точку и наклон. В первом случае, чтобы построить прямую линию, необходимо выбрать две точки на плоскости и провести через них прямую. Во втором случае, для построения нужно выбрать начальную точку и задать наклон прямой, носящийся в качестве соотношения между вертикальным и горизонтальным направлениями.

Параллельные линии - это линии, которые не пересекаются, но лежат в одной плоскости и сохраняют постоянное расстояние друг от друга. Построение параллельных линий возможно при помощи специальных методов, таких как угловой способ или метод с использованием параллельных нитей.

В данной статье рассмотрены основные конструкции и алгоритмы построения прямых и параллельных линий с применением различных методов. Правильное использование этих навыков поможет вам в решении геометрических задач и приложении их в практике.

Способы построения прямых линий и их алгоритмы

1. Построение прямой линии по двум точкам:

1. Выберите две точки на плоскости, через которые должна проходить прямая.
2. Соедините эти точки прямой линией, используя линейку или другое подходящее инструментальное средство.

2. Построение прямой линии по углу наклона и точке:

1. Выберите точку на плоскости, через которую должна проходить прямая.
2. Определите угол наклона, под которым должна быть построена прямая линия.
3. Используя линейку и угольник, постройте прямую линию с заданным углом наклона и проходящую через выбранную точку.

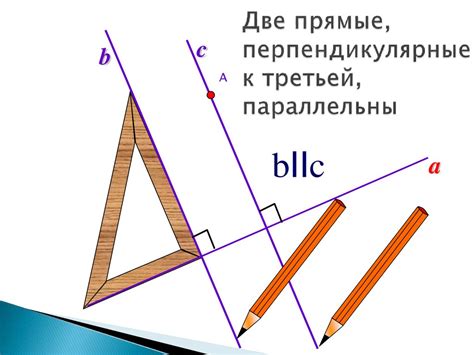
3. Построение параллельной линии:

1. Выберите точку на плоскости, через которую должна проходить исходная линия.
2. Используя линейку, постройте перпендикуляр к исходной линии через выбранную точку.
3. Используя угольник, определите угол наклона, под которым должна быть построена параллельная линия.
4. Постройте прямую линию с заданным углом наклона, проходящую через выбранную точку. Эта линия будет параллельна исходной линии.

Каждый из указанных способов имеет свои преимущества и может быть использован для решения различных геометрических задач. Знание этих способов позволяет строить прямые линии с высокой точностью и эффективностью.

Метод построения прямых линий с помощью линейки и циркуля

Процесс построения прямых линий с использованием линейки и циркуля состоит из следующих шагов:

1. Установите одну плоскую сторону линейки параллельно уже имеющейся линии или двум заданным точкам.
2. Закрепите линейку таким образом, чтобы она не двигалась.
3. Установите циркуль в одной из заданных точек или на начале уже имеющейся линии.
4. Регулируйте ширину циркуля, чтобы его концы находились на нужном расстоянии от центра.
5. Совершите поворот циркуля вокруг центра, прокрутите его на 360 градусов.
6. Проведите прямую линию через концы циркуля.

Таким образом, путем повторения указанных шагов можно построить необходимое количество прямых линий параллельно уже имеющейся линии или между заданными точками.

Метод построения прямых линий с помощью линейки и циркуля является универсальным и обладает высокой точностью. Он широко используется в геометрии, архитектуре и инженерных расчетах для построения различных фигур и конструкций.

Алгоритм построения параллельных линий с использованием угломера

1. Выбрать точку P, через которую будет проходить параллельная линия.
2. Установить угломер в точку P и провести линию через точку Q1, которая является начальной точкой параллельной линии и расположена на исходной линии.
3. Установить угломер в точку P и провести линию через точку Q2, которая является конечной точкой параллельной линии и также расположена на исходной линии.
4. Точки Q1 и Q2 на исходной линии будут являться начальными точками параллельной линии, а линия, проходящая через них, будет параллельна исходной линии.

Таким образом, алгоритм построения параллельных линий с использованием угломера позволяет легко и эффективно конструировать параллельные линии, сохраняя их геометрические свойства.