Рациональная функция – это функция, представляющая собой отношение двух многочленов. Как построить такую функцию правильно? Для этого нам понадобится знание основных шагов и правил.
Первый шаг – определить область определения функции. Область определения – это множество значений аргумента, при которых функция определена. Помни, что в знаменателе рациональной функции не должно быть нулей. Также обрати внимание на вертикальные асимптоты – значения, которые функция стремится к бесконечности.
Следующий шаг – разложить функцию на простейшие дроби. Для этого расскажем о методе неопределенных коэффициентов. Представь функцию в виде суммы неопределенных слагаемых. Подбери значения неизвестных коэффициентов так, чтобы слева и справа от равенства стояли одинаковые выражения. Решив систему уравнений, найди эти значения.
Не забудь проверить полученные слагаемые. Приведи их к общему знаменателю и сделай упрощение. Помни также о вертикальных и наклонных асимптотах. После этих шагов ты можешь быть уверен, что построение рациональной функции прошло без ошибок.
План:
Шаг 1: Определить асимптоты рациональной функции.
Шаг 2: Найти корни числителя и знаменателя функции.
Шаг 3: Определить знак функции на каждом интервале между корнями.
Шаг 4: Найти точки разрыва функции и определить их типы.
Шаг 5: Найти значения функции в выбранных точках.
Шаг 6: Построить график функции, учитывая полученные данные.
Подготовка к построению рациональной функции:

Для успешного построения рациональной функции необходимо выполнить ряд предварительных действий:
- Определить область определения функции. Для рациональной функции вида f(x) = P(x)/Q(x), где P(x) и Q(x) - многочлены, область определения - это множество значений переменной x, при которых знаменатель Q(x) не равен нулю.
- Упростить функцию. Для удобства построения и анализа графика рациональной функции рекомендуется сократить все дроби наибольшим общим делителем числителя и знаменателя. Также можно попытаться сократить функцию до простейшего вида.
- Найти асимптоты функции. Рациональная функция может иметь горизонтальные, вертикальные и наклонные асимптоты. Горизонтальная асимптота существует, если степень числителя P(x) меньше или равна степени знаменателя Q(x). Вертикальные асимптоты возникают, когда знаменатель Q(x) обращается в нуль. Наклонные асимптоты могут существовать при определенных условиях и вычисляются с помощью деления многочленов.
- Определить точки пересечения с осями координат. Для этого решаем уравнение функции f(x) = 0 и находим значения x, для которых функция пересекает ось OX (горизонтальная ось) или ось OY (вертикальная ось).
- Применить методы анализа функций для определения интервалов монотонности, экстремумов и точек перегиба.
- Построить график функции на координатной плоскости, используя полученные выше данные. Важно правильно отметить все найденные особые точки (асимптоты, точки пересечения и т.д.), а также учесть особенности поведения функции в разных интервалах.
После выполнения всех указанных шагов вы будете готовы успешно построить рациональную функцию и анализировать ее свойства.
Шаги построения рациональной функции
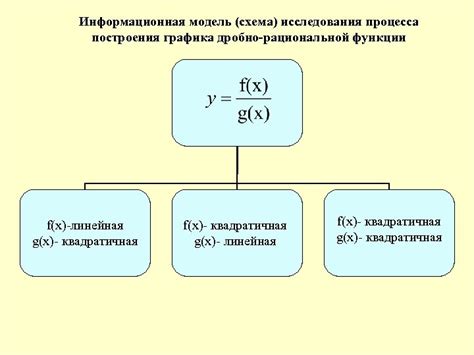
Чтобы построить рациональную функцию правильно, следуйте следующим шагам:
- Определите область определения функции. Это значения переменной, для которых функция определена. Например, функция может быть не определена при определенных значениях в знаменателе.
- Примените правила сокращения. Если в числителе и знаменателе есть общие множители, их можно сократить и записать в виде произведения из множителей.
- Разложите знаменатель на множители. Если функция не имеет кратных корней в знаменателе, разложите знаменатель на простые множители. Если функция имеет кратные корни, разложите знаменатель на степенные множители.
- Запишите разложение в виде суммы или разности дробей с действительными или комплексными коэффициентами.
- Определите вертикальные асимптоты. Это вертикальные линии, которые функция приближается к непрерывной линии при стремлении аргумента к бесконечности или минус бесконечности. Определите их, используя значения переменной, при которых знаменатель равен нулю, но числитель не равен нулю.
- Определите горизонтальные или наклонные асимптоты. Это непрерывные линии, к которым функция приближается при стремлении аргумента к бесконечности или минус бесконечности. Определите их, используя степени числителя и знаменателя.
- Определите точки пересечения с осями координат. Это значения переменной, при которых функция пересекает оси координат, то есть когда числитель равен нулю и знаменатель не равен нулю.
- Постройте график функции, используя полученную информацию о вертикальных и горизонтальных асимптотах, а также точках пересечения с осями координат.
Следуя этим шагам, вы сможете построить рациональную функцию правильно и без ошибок. Не забывайте проверить полученный график с использованием математического программного обеспечения или графического калькулятора.
Проверка наличия ошибок и корректировка рациональной функции
Проверка наличия ошибок
Перед тем, как приступить к корректировке рациональной функции, необходимо провести проверку на наличие ошибок. Важно убедиться, что функция правильно записана и не содержит неправильных символов или отсутствующих элементов.
Первым шагом проверки является анализ знаменателя функции. Необходимо проверить, содержит ли он переменные, и если да, то убедиться в их корректной записи. Также важно проверить, нет ли знаменателе нулевых значений или других значений, при которых функция может стать неопределенной.
Затем следует проверить числитель функции. Анализируя его, нужно удостовериться, что все переменные правильно записаны и соответствуют знаменателю функции. Также важно провести проверку на возможность сокращения дроби или упрощения выражения.
Также стоит обратить внимание на наличие других ошибок, таких как неправильное расположение скобок, ошибки в знаках операций или упущенные элементы. Обнаружив ошибки, необходимо приступить к их исправлению.
Корректировка рациональной функции
После тщательной проверки функции и обнаружении ошибок, можно приступить к их исправлению. Для этого необходимо следовать указанным ниже шагам:
- Выделить основные элементы функции, такие как числитель и знаменатель.
- Проверить наличие сокращений или упрощений, которые можно применить к каждому из элементов. Например, рациональные функции могут иметь общие множители в числителе и знаменателе, которые могут быть сокращены.
- Проверить правильность записи каждого элемента функции. Убедиться, что все переменные написаны корректно и соответствуют друг другу.
- Избавиться от ошибок в виде неправильного расположения скобок, ошибок в знаках операций или упущенных элементов. Внимательно просмотреть каждый элемент функции и исправить обнаруженные ошибки.
- Провести финальную проверку функции, чтобы убедиться, что все ошибки исправлены и запись функции является правильной.
После завершения процесса проверки и корректировки, можно с уверенностью использовать рациональную функцию в нужных математических операциях и вычислениях.