Ромб – это уникальная геометрическая фигура со специфическими свойствами. Для его построения можно использовать различные методы, включая конструирование по стороне и диагонали. В данной статье мы подробно рассмотрим процесс построения ромба с использованием этих двух параметров. Если вы интересуетесь геометрией и желаете научиться строить ромб, то предлагаем вам следовать нашим подробным инструкциям.

Конструирование ромба по стороне и диагонали: для начала нам необходимо знать значения стороны и диагонали ромба. По этим данным мы сможем строить их взаимосвязь и получать точные результаты. Стоит отметить, что ромб – это четырехугольник, у которого все стороны равны между собой. Каждая диагональ ромба является осью симметрии для него и делит его на два равных треугольника.

Шаг 1: проведите линию, которая будет соответствовать стороне ромба. Укажите на этой линии точку, которую назовем вершиной ромба.

Алгоритм построения ромба по стороне и диагонали: подробная инструкция

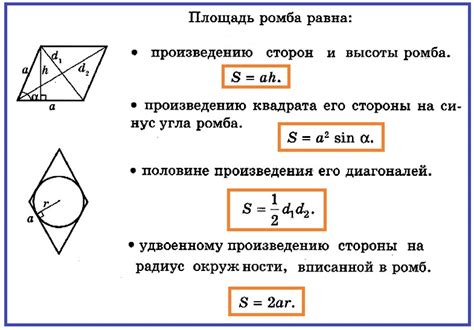
1. Назовем данную сторону и диагональ а и d соответственно.
2. С использованием линейки и карандаша нарисуйте отрезок длиной а.
3. Отметьте на этом отрезке середину и обозначьте ее буквой M.
4. Из точки M проведите перпендикуляр к этому отрезку.
5. Установите циркуль на длине половины диагонали (d/2) и воспользуйтесь им для построения окружности с центром в точке M. Эта окружность будет проходить через точки, где искомая диагональ пересекается со стороной.
6. С той же точки M проведите отрезок до одной из точек пересечения окружности с основанием.
7. Теперь используя отрезок, соединяющий точку M и отмеченную выше точку пересечения, и циркуль с радиусом, равным диагонали, постройте окружность с центром в точке пересечения.
8. Точки пересечения второй окружности с основанием ромба являются оставшимися вершинами искомого ромба.
9. Теперь с помощью линейки и карандаша соедините вершины ромба и получите завершенную фигуру.

Следуя этому алгоритму, можно успешно построить ромб по известным стороне и диагонали. Важно быть аккуратным и точным в измерениях, чтобы получить правильный результат.

Шаг 1: Определение длины стороны и диагонали

Прежде чем мы сможем начать конструирование ромба, нам необходимо определить длину его стороны и диагонали.

Длина стороны ромба обозначается обычно символом "a". Можно явно знать значение "a", или его можно найти, зная другие параметры ромба, такие как длина диагонали или угол.

Также, нам потребуется знать длину одной из диагоналей ромба. Диагональ ромба обозначается символами "d1" и "d2". Обычно длины диагоналей ромба равны. Если одна диагональ известна, то другая диагональ может быть найдена по формуле: d2 = √(4a^2 - d1^2), где "a" - длина стороны ромба.

Таким образом, определение длины стороны и диагонали ромба - важный первый шаг в его конструировании.

Шаг 2: Расчет угла и диагоналей

Для конструирования ромба по заданной стороне и диагонали необходимо рассчитать угол между стороной и диагональю, а также значения диагоналей ромба.

Для расчета угла между стороной и диагональю можно использовать теорему косинусов. Обозначим сторону ромба как "a" и диагональ как "d". Угол "α" будет являться углом между стороной и диагональю. Тогда теорема косинусов имеет вид:

cos(α) = (d^2 - 2a^2) / (2a^2)

Решая эту формулу относительно угла "α", получим:

α = arccos((d^2 - 2a^2) / (2a^2))

Рассчитав значение угла "α", можно найти значения диагоналей ромба, используя теорему синусов. Обозначим значение одной из диагоналей как "D". Теорема синусов имеет вид:

sin(α) = D / d

Решая эту формулу относительно диагонали "D", получим:

D = d * sin(α)

Зная значение угла "α" и одну из диагоналей "D", можно найти вторую диагональ, используя свойства ромба, согласно которым диагонали ромба равны и перпендикулярны друг другу.

Используя полученные значения угла и диагоналей, можно приступить к следующему шагу - построению ромба.

Шаг 3: Конструирование ромба

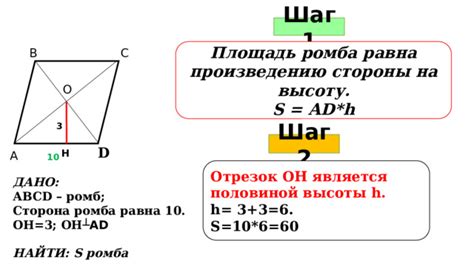
Теперь, когда у нас есть отрезок AB и его диагональ BD, мы можем перейти к фактической конструкции ромба.

1. Найдите середину диагонали BD. Это можно сделать, разделив диагональ пополам. Обозначим ее точкой M.

2. С помощью циркуля и линейки проведите прямую, проходящую через точку M и перпендикулярно диагонали BD. Обозначим точки пересечения этой прямой с отрезком AB и AC как точки N и O соответственно.

3. Используя линейку, проведите отрезок NO.

4. Отметьте середины отрезков AB, BC, CD и DA и обозначьте их, соответственно, точками P, Q, R и S.

5. Проведите прямые через точки N, O и M, пересекающиеся соответственно с точками P, Q, R и S. Пересечение этих прямых даст нам вершины ромба.

6. С помощью линейки и циркуля постройте остальные стороны ромба, соединяя вершины между собой и с центром M.

7. Убедитесь, что все стороны ромба равны друг другу, и что прямые, соединяющие противоположные вершины, перпендикулярны друг другу.

Теперь у вас есть полностью построенный ромб с известной стороной и диагональю. Пользуйтесь этой конструкцией для решения задач и определения других характеристик ромба.

Шаг 4: Проверка правильности построения

После завершения построения ромба нужно убедиться в его правильности. Существует несколько способов проверить, что ромб построен корректно.

1. Проверка сторон. Проверьте длины всех сторон ромба с помощью линейки или другого измерительного инструмента. Все стороны ромба должны иметь одинаковую длину. Если длины сторон различаются, возможно, что вы совершили ошибку при измерении или построении.
2. Проверка диагоналей. Измерьте длины обеих диагоналей ромба. Диагонали должны быть равны и пересекаться в центре ромба. Если длины диагоналей различаются или они не пересекаются в точке, скорее всего, вы допустили ошибку при построении ромба.
3. Проверка углов. Проверьте все углы ромба с помощью угломера или другого инструмента для измерения углов. Все углы ромба должны быть одинаковыми и равняться 90 градусам. Если углы отличаются или не равны 90 градусам, возможно, что вы неправильно построили ромб.

Если при проверке вы обнаружили несоответствия, повторите построение ромба, следуя шагам инструкции. Тщательно проверьте каждый шаг и измерение, чтобы исключить возможные ошибки. Правильно построенный ромб будет иметь равные длины всех сторон, равные длины диагоналей и углы в 90 градусов.