Сечение куба – это плоская фигура, которая образуется, когда плоскость пересекает куб. Построение сечения может показаться сложной задачей, особенно если имеется только три точки на плоскости и необходимо найти соответствующую плоскость. В данном руководстве мы рассмотрим простой и эффективный способ построения сечения куба через три заданные точки.
Прежде чем начать, важно понять основные принципы построения сечений. Сечение должно проходить через каждую из трех точек, и плоскость, которую мы построим, должна пересекать все грани куба. Для начала, выберите одну из точек и обозначьте ее как вершину куба. Затем подберите две другие точки и проведите через них прямую. Далее, подберите точку на прямой и проведите через нее плоскость, перпендикулярную прямой.
Теперь, когда у вас есть плоскость, проходящая через заданные три точки, следует проверить, пересекает ли она все грани куба. Если плоскость пересекает все грани, то сечение куба построено верно. В противном случае, вам необходимо изменить положение плоскости и провести ее повторно через заданные точки, пока не будет достигнут желаемый результат.
Определение куба и его особенности
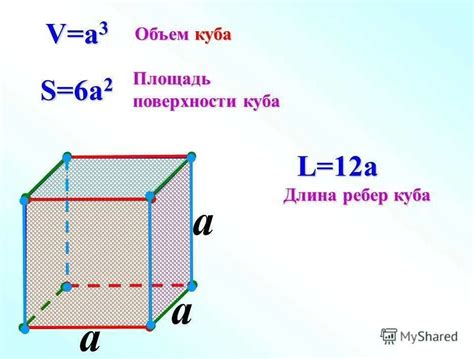
- Куб является правильным полиэдром, то есть все его грани являются равными правильными многоугольниками.
- У куба шесть граней, каждая из которых является квадратом.
- Все его ребра и углы являются равными друг другу.
- Куб обладает симметрией, поскольку имеет 12 осей симметрии и 24 центра симметрии.
- Куб является пространственной фигурой, то есть обладает трехмерной формой.
- Объем куба вычисляется по формуле V = a^3, где а - длина ребра куба.
- Площадь поверхности куба вычисляется по формуле S = 6a^2, где а - длина ребра куба.
Куб является одним из наиболее известных и часто используемых геометрических тел, применяемых в архитектуре, инженерии, математике и других областях науки и техники.
Система координат и выбор точек
Для построения сечения куба через 3 точки необходимо использовать систему координат, чтобы определить положение и взаимное расположение точек. Система координат в трехмерном пространстве состоит из осей: x, y и z.
Первым шагом необходимо выбрать три точки, через которые будет проходить сечение куба. Эти точки должны быть расположены в трехмерном пространстве и быть линейно независимыми. Рекомендуется выбирать точки таким образом, чтобы они лежали на разных сторонах куба и были представительными для его формы.
Для удобства выбора точек можно использовать следующие методы:
- Графический метод: нарисовать куб на листе бумаги и отметить на нем нужные точки. Затем можно измерить координаты этих точек на рисунке.
- Использование программного обеспечения: с помощью специализированных программ можно создать трехмерную модель куба и произвести выбор точек с помощью инструментов для работы с моделью.
- Математический метод: использовать формулы для определения координат нужных точек, исходя из их расстояния от центра куба и углов, по которым они расположены.
Независимо от выбранного метода, важно удостовериться, что выбранные точки корректно определяют сечение куба и что они не совпадают или не лежат на одной прямой. Это гарантирует уникальность и корректность сечения.
Нахождение плоскости сечения

Для построения сечения куба через три точки необходимо найти плоскость, проходящую через эти точки. Для этого можно воспользоваться методом нахождения уравнения плоскости по трем точкам.
Уравнение плоскости в трехмерном пространстве имеет вид:
| Ax + By + Cz + D = 0 |
Где (x, y, z) - произвольная точка на плоскости, A, B, C - коэффициенты плоскости, D - свободный член.
Для нахождения коэффициентов плоскости по трем точкам необходимо воспользоваться следующей системой уравнений:
| Ax1 + By1 + Cz1 + D = 0 |
| Ax2 + By2 + Cz2 + D = 0 |
| Ax3 + By3 + Cz3 + D = 0 |
Где (x1, y1, z1), (x2, y2, z2), (x3, y3, z3) - координаты заданных точек.
Решая эту систему уравнений методом Крамера или другими методами, можно найти значения коэффициентов A, B, C и D уравнения плоскости. Получившиеся значения можно подставить в уравнение плоскости и использовать для построения сечения куба через заданные точки.
Построение сечения куба через 3 точки
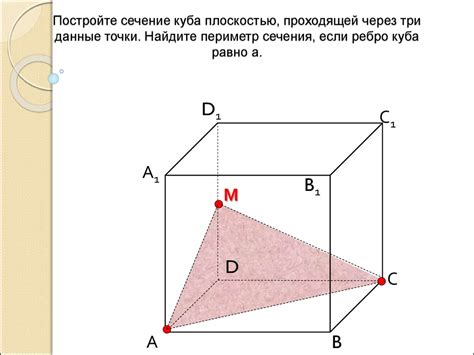
Для построения сечения куба через 3 точки необходимо выполнить следующие шаги:
1. Определить координаты трех точек, через которые будет проходить сечение.
2. Проверить, что заданные точки лежат на ребрах куба. Если точки не лежат на ребрах куба, то построение сечения невозможно.
3. Найти плоскость, проходящую через заданные точки. Для этого можно воспользоваться методом определения плоскости по трём точкам.
4. Построить сечение куба путем пересечения найденной плоскости с ребрами и гранями куба. Для этого необходимо найти точки пересечения плоскости с ребрами и гранями куба.
5. Отобразить полученное сечение на рисунке или в трехмерном пространстве. Можно использовать программные инструменты для трехмерного моделирования, чтобы наглядно представить результат.
Построение сечения куба через 3 точки представляет собой задачу из области геометрии и требует аккуратности при определении координат точек и вычислении пересечений. Внимательное выполнение каждого шага позволит получить точное сечение, которое можно использовать в дальнейшей работе.
Примеры применения сечения куба
- Строительство: Сечение куба используется в архитектуре для создания планов зданий и их детализации. Оно позволяет точно определить расположение стен, окон, дверей и других элементов конструкции.
- Дизайн интерьера: Сечение куба используется дизайнерами интерьера для визуализации планировок помещений. Это помогает клиентам лучше представить, как будет выглядеть их будущий интерьер и принять более обоснованные решения.
- Образование: Применение сечения куба расширяет понимание геометрии учащихся. Они могут увидеть, как плоскость пересекает трехмерный объект и визуализировать его на плоском изображении.
- 3D-моделирование: Сечение куба является важной техникой в 3D-моделировании. Позволяет вырезать и удалять ненужные части модели и улучшает ее визуализацию.
- Научные исследования: Сечение куба применяется в различных научных исследованиях, таких как физика и математика. Это позволяет лучше понять структуру и свойства объектов и использовать полученные результаты в различных областях науки.