Серединный перпендикуляр - это линия, которая перпендикулярна одной из сторон треугольника и проходит через середину этой стороны. В равнобедренном треугольнике серединный перпендикуляр проходит через эту сторону и через вершину, противоположную ей. Нахождение такой линии может быть полезно при решении различных геометрических задач. В этой статье мы рассмотрим пошаговую инструкцию о том, как найти серединный перпендикуляр в равнобедренном треугольнике.
Шаг 1: Прежде чем начать, убедитесь, что у вас есть равнобедренный треугольник. Равнобедренный треугольник имеет две равные стороны и два равных угла, образованных этими сторонами.
Шаг 2: Выберите одну из сторон треугольника, через которую будет проходить серединный перпендикуляр. Обозначим эту сторону как AB.
Шаг 3: Найдите середину стороны AB и обозначьте ее как точку M.
Шаг 4: Постройте отрезок MC, где C - вершина треугольника, противоположная стороне AB.
Шаг 5: Используя циркуль или компас, установите радиус, равный длине отрезка MC.
Шаг 6: С центром в точке M и радиусом MC проведите дугу, пересекающую сторону AB в точках N и O.
Шаг 7: Проведите прямую, проходящую через точки N и O. Эта прямая будет серединным перпендикуляром стороны AB.
Теперь вы знаете, как найти серединный перпендикуляр в равнобедренном треугольнике. Этот метод можно использовать для решения различных геометрических задач, связанных с равнобедренными треугольниками.
Определение серединного перпендикуляра
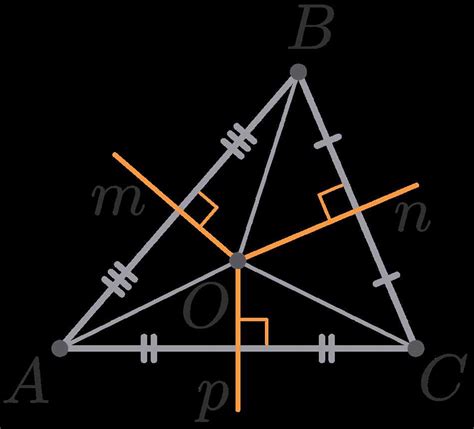
Чтобы найти серединный перпендикуляр, нужно выполнить следующие шаги:
- Найдите точку пересечения серединных перпендикуляров двух сторон треугольника. Эта точка является серединой базовой стороны треугольника и называется вершиной.
- Проведите прямую линию через вершину и точку пересечения серединных перпендикуляров.
- Эта прямая линия является серединным перпендикуляром и делит треугольник на две равные части.
Серединные перпендикуляры в равнобедренном треугольнике имеют важное геометрическое свойство: они пересекаются в одной точке, которая называется центром вписанной окружности. Центр вписанной окружности является центром симметрии треугольника и имеет радиус, равный половине длины базовой стороны треугольника.
Что такое серединный перпендикуляр в равнобедренном треугольнике и как он определяется
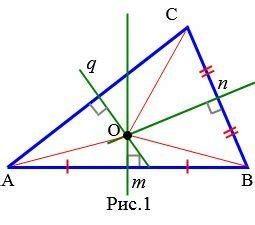
Чтобы определить серединный перпендикуляр в равнобедренном треугольнике, можно выполнить следующие шаги:
- На основе треугольника найдите середину основания. Это точка, которая делит основание пополам.
- Из середины основания проведите линию, которая будет перпендикулярна к основе. Для этого используйте рисовку перпендикуляра или угломер или проведите две равные линии под углами 90 градусов одна к другой.
- Продолжите эту линию до вершины треугольника. Серединный перпендикуляр должен проходить через вершину и делить основание пополам.
Серединный перпендикуляр в равнобедренном треугольнике является важным элементом, который помогает найти другие линейные или угловые свойства этого треугольника, такие как биссектрисы углов или высоты треугольника.
Нахождение точки пересечения
Чтобы найти точку пересечения серединного перпендикуляра в равнобедренном треугольнике, нужно:
- Найти середину основания треугольника. Для этого можно взять половину длины основания и отложить от вершины треугольника.
- Провести через найденную середину основания линию, перпендикулярную основанию треугольника. Для этого можно использовать угломер и циркуль.
- Провести серединный перпендикуляр к боковой стороне треугольника. Для этого нужно рассмотреть середину боковой стороны и провести перпендикуляр к ней.
- Найденные линии пересекаются в точке, которая является серединой основания треугольника и точкой пересечения серединного перпендикуляра и боковой стороны.
Таким образом, точка пересечения находится путем проведения перпендикулярных линий и определения их пересечения.
Для наглядного представления можно представить данную процедуру в виде таблицы:
| Шаг | Описание |
|---|---|
| Шаг 1 | Находим середину основания треугольника |
| Шаг 2 | Проводим перпендикуляр к основанию через найденную середину |
| Шаг 3 | Находим середину боковой стороны треугольника |
| Шаг 4 | Проводим перпендикуляр к боковой стороне через найденную середину |
| Шаг 5 | Найденные линии пересекаются в точке пересечения |
Нахождение середины основания

- Проведите линию, соединяющую две вершины основания треугольника - это будет основание перпендикуляра.
- Используя линейку или циркуль, найдите середину этой линии. Серединная точка будет серединой основания треугольника.
- Пометьте эту точку, чтобы использовать ее в дальнейшем для построения серединного перпендикуляра.
Найдя середину основания, вы можете продолжить ваше изучение и построение серединного перпендикуляра в равнобедренном треугольнике.
Построение перпендикуляра

Чтобы построить серединный перпендикуляр в равнобедренном треугольнике, следуйте этим шагам:
- Найдите середину одной из сторон треугольника. Для этого отметьте равные отрезки, проведя две половинки этой стороны.
- Возьмите циркуль и отметьте равные расстояния от середины этой стороны до каждого из вершин треугольника. Обозначьте эти точки как A и B.
- На самом расстоянии между точками A и B поставьте острый карандаш и проведите окружность.
- Опустите перпендикулярную линию, проходящую через центр окружности.
- Повторите те же шаги для другой стороны треугольника.
В результате вы получите перпендикуляр, проходящий через середину одной из сторон треугольника и пересекающийся с перпендикуляром, проходящим через середину другой стороны.
Измерение длины перпендикуляра
Для того чтобы найти серединный перпендикуляр в равнобедренном треугольнике, вам понадобится измерить длину перпендикуляра при помощи линейки или другого инструмента для измерения. Вот пошаговая инструкция:
- Выберите одну из сторон равнобедренного треугольника, отметьте середину этой стороны и обозначьте ее точкой O.
- Выберите любую точку на третьей стороне треугольника (не являющейся базовой стороной) и обозначьте ее точкой P.
- С помощью линейки измерьте расстояние от точки O до точки P, это будет длина перпендикуляра.
Помните, что в равнобедренном треугольнике серединный перпендикуляр будет равен половине длины третьей стороны треугольника, и измеренная вами длина должна быть равна этой величине.
После измерения длины перпендикуляра вы можете использовать эту информацию для нахождения серединного перпендикуляра и построения его на плоскости.
Нахождение середины гипотенузы

Для нахождения середины гипотенузы в равнобедренном треугольнике следуйте указанным ниже шагам:
Шаг 1: Найдите длину гипотенузы треугольника. Для этого можно использовать теорему Пифагора или другую известную формулу для вычисления длины гипотенузы.
Шаг 2: Разделите длину гипотенузы на 2, чтобы найти середину. Например, если длина гипотенузы составляет 10 единиц, то середина будет находиться на 5 единиц от начала.
Шаг 3: Используйте полученную длину середины гипотенузы для нанесения отметки на гипотенузу. Используйте линейку или другой инструмент для точного измерения.
Шаг 4: Проведите перпендикуляр к гипотенузе из места, где была сделана отметка середины. Перпендикуляр будет проходить через середину гипотенузы и быть параллельным основанию треугольника.
Теперь вы знаете, как найти середину гипотенузы в равнобедренном треугольнике. Этот метод позволяет определить точку, в которой пересекаются середины гипотенуз и основания треугольника, что может быть полезно при решении различных геометрических задач.
Проверка полученных результатов

После того, как мы построили серединный перпендикуляр в равнобедренном треугольнике, нужно убедиться, что полученное решение верное. Это можно сделать с помощью следующих шагов:
- Возьмите линейку и измерьте расстояние от вершины треугольника до середины основания.
- Затем измерьте расстояние от середины основания до середины стороны треугольника.
- Если эти два измерения равны, то полученный перпендикуляр является серединным.
- Если измерения отличаются, проверьте выполнение предыдущих шагов и повторите их, чтобы убедиться, что не допущено ошибок.
Проверка полученных результатов поможет убедиться в правильности построения серединного перпендикуляра. Если все шаги выполнены правильно, то можно быть уверенным в корректности результата.
Свойства серединного перпендикуляра
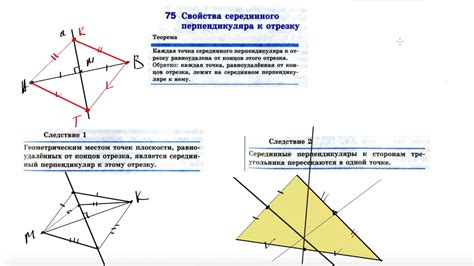
| Свойство | Описание |
| 1 | Серединный перпендикуляр является линией симметрии равнобедренного треугольника. |
| 2 | Серединный перпендикуляр делит основание треугольника на две равные части. |
| 3 | Серединный перпендикуляр перпендикулярен к основанию треугольника. |
| 4 | Точка пересечения серединного перпендикуляра и основания треугольника является серединой основания. |
Свойства серединного перпендикуляра позволяют использовать его для решения различных задач, связанных с равнобедренными треугольниками.