Как построить середину отрезка Пифагорий 1.12 — простая инструкция для всех

Середина отрезка Пифагорий 1.12 – одна из ключевых точек в геометрии, пересекающая гипотенузу заданного прямоугольного треугольника, разделяя ее на две равные части. Построение этой точки может показаться сложным делом, но на самом деле оно основано на простом алгоритме, состоящем из нескольких шагов.

Первым шагом в построении середины отрезка Пифагорий 1.12 является определение середины гипотенузы. Для этого необходимо измерить длину гипотенузы с помощью линейки или сантиметровой ленты, а затем поделить полученное значение пополам. Полученная точка будет серединой гипотенузы и одной из точек конструкции середины отрезка Пифагорий 1.12.

Далее, вторым шагом, необходимо провести прямую, соединяющую середину гипотенузы и вершину прямого угла треугольника. Для этого можно использовать циркуль или линейку, приложив ее к середине гипотенузы и вершине прямого угла. Полученная прямая будет перпендикулярна гипотенузе и проходить через середину гипотенузы.

Как найти середину отрезка Пифагорий 1.12: инструкция и шаги

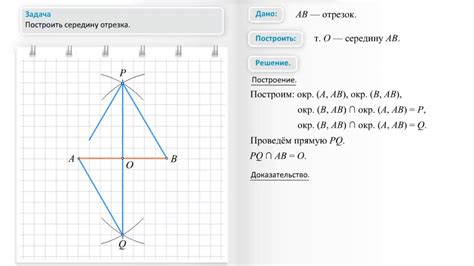
Шаг 1: Отметьте на прямой оси две точки: точку А с координатами 1 и точку Б с координатами 12.

Шаг 2: Посчитайте разницу между координатами точек А и Б по оси:

Разница = Координата Б - Координата А

Шаг 3: Разделите полученную разницу на два:

Середина = Разница / 2

Шаг 4: Добавьте полученное значение середины к координате точки А, чтобы найти координату середины отрезка Пифагорий 1.12:

Координата середины = Координата А + Середина

Теперь вы знаете, как найти середину отрезка Пифагорий 1.12 с помощью этих простых шагов!

Определение математического понятия "середина отрезка"

Для определения середины отрезка необходимо взять две конечные точки и найти точку, которая равноудалена от них. Эта точка делит отрезок пополам и является его серединой.

Математически, середина отрезка находится как среднее арифметическое координат двух конечных точек отрезка.

Середины отрезков широко используются в математике, физике, геометрии и других науках для решения различных задач и вычислений. Они являются важными концепциями в геометрии и помогают в различных вычислениях, конструированиях и моделировании объектов и явлений.

Понятие "отрезок Пифагорий 1.12" и его особенности

Основной особенностью отрезка Пифагорий 1.12 является его равенство двум отрезкам: начальному отрезку Пифагорий 1.1 и конечному отрезку Пифагорий 1.2. То есть, если отрезок Пифагорий 1.12 делится точкой своей середины, то получаются два равных отрезка. Обозначается данное равенство как AB = BC.

Другой важной особенностью отрезка Пифагорий 1.12 является его положение на прямой линии. Он всегда находится между начальной и конечной точками и делит прямую на две части: начальную и конечную. Это деление прямой называется также делением на равные отрезки.

Отрезок Пифагорий 1.12 активно используется в геометрии и алгебре. Он является основой для решения многих задач и упрощает расчеты при работе с отрезками. Изучение свойств и особенностей этого отрезка позволяет более эффективно решать задачи и строить точные геометрические фигуры.

Первый шаг: построение правильного треугольника

Чтобы построить правильный треугольник, нужно:

1. Нарисовать отрезок длиной 1.12 единицы.
2. Взять точку A на этом отрезке в качестве центра.
3. На отрезке AC, одном из концов которого является точка A, отложить отрезок AD длиной, равной 1 единице.
4. Соединить точку D с точкой C.
5. Точка D станет вершиной правильного треугольника.

Теперь у вас есть правильный треугольник со стороной 1 и углами, равными 60 градусам. Завершение следующих шагов поможет построить середину отрезка Пифагория 1.12.

Второй шаг: поиск середины отрезка в правильном треугольнике

Для этого проведем высоту CD, перпендикулярную стороне AB. Точка D будет серединой отрезка AB.

Для нахождения середины отрезка AB воспользуемся формулой:

Где x_A, x_B, y_A, y_B - координаты точек A и B соответственно.

Если изначально даны значения координат (x_A, y_A) и (x_B, y_B), то подставив их в формулу, мы получим координаты точки D, которая будет серединой отрезка AB в треугольнике ABC.