Шестиугольник – это многоугольник, который имеет шесть сторон и шесть углов. Его особенностью является, что все стороны и углы являются равными. Построение шестиугольника – увлекательная задача, требующая определенных математических навыков и знаний. Одним из самых интересных способов построения шестиугольника является его размещение вокруг окружности.
Для построения шестиугольника вокруг окружности, мы будем использовать некоторые свойства и теоремы геометрии. Во-первых, нам понадобится понимание круга и окружности. Круг – это множество точек, расположенных на одной плоскости и на равном расстоянии от одной точки, называемой центром круга. Окружность – это граница круга, то есть линия, на которой все точки равноудалены от центра. Окружность можно построить, используя центр и радиус – расстояние от центра до любой точки на окружности.
Теперь, когда мы понимаем понятия круга и окружности, можно приступить к построению шестиугольника вокруг окружности. Для начала, построим окружность с известным радиусом, который будет определять размеры будущего шестиугольника. Затем, найдем центр окружности – это будет точка, через которую пройдут все шестиугольники, вписанные в эту окружность.
Построение шестиугольника вокруг окружности
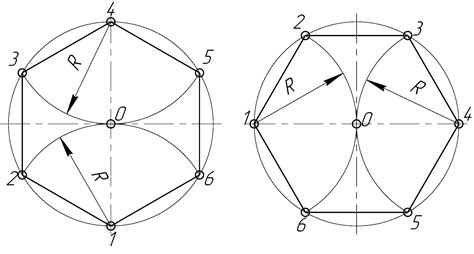
- Найдите центр окружности и отметьте его.
- Выберите одну из точек на окружности и отметьте ее.
- Соедините центр окружности с отмеченной точкой.
- Повторите предыдущие два шага для следующей точки на окружности.
- Повторите шаги 2-4 до тех пор, пока все точки на окружности не будут соединены с центром.
В результате выполнения алгоритма вы получите шестиугольник, каждая из сторон которого будет соединять центр окружности с одной из точек на окружности.
Построение шестиугольника вокруг окружности может быть полезно в различных сферах, включая геометрию, архитектуру и дизайн. Эта фигура имеет особую симметрию и эстетическую привлекательность.
Необходимость строить шестиугольник вокруг окружности может возникнуть, например, при решении задач связанных с размещением объектов вокруг центральной точки или при создании геометрических узоров.
Таким образом, построение шестиугольника вокруг окружности является важной задачей геометрии и может быть произведено с использованием простого алгоритма, описанного выше.
Инструменты для построения

Для построения шестиугольника вокруг окружности вам потребуются следующие инструменты:
- Компас: основной инструмент для создания окружности, вокруг которой будет построен шестиугольник. Он позволяет точно измерять и рисовать окружности нужного размера.
- Линейка: поможет вам провести отрезки, чтобы построить шестиугольник внутри окружности. Она поможет осуществить процесс максимально точно и аккуратно.
- Карандаш: для рисования и маркировки точек и линий.
- Ластик: пригодится для исправления ошибок или подчистки конечного результата.
При работе с инструментами помните о точности и аккуратности, чтобы построить шестиугольник, который идеально вписывается в окружность.
Установка радиуса окружности
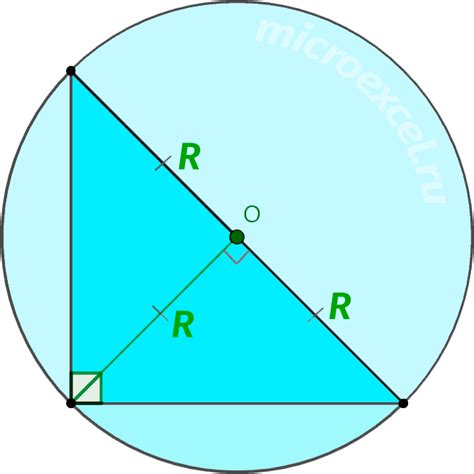
Установить радиус можно различными способами. Рассмотрим один из них:
1. Возьмите линейку или штангенциркуль и измерьте требуемое расстояние. Например, предположим, что необходимо установить радиус окружности равным 5 сантиметрам. Поместите ноль линейки или штангенциркуля в центр будущей окружности и отмерьте 5 сантиметров, затянув противоположную сторону линейки или штангенциркуля.
2. Определите центр окружности. Чтобы построить шестиугольник вокруг окружности, необходимо знать точное местоположение центра окружности. С помощью линейки или штангенциркуля отметьте точку на бумаге, которая будет являться центром окружности.
3. Нанесите окружность на бумаге вокруг этой точки, используя установленный радиус. Поставьте один конец линейки или штангенциркуля на центр окружности и создайте круг, перемещая другой конец инструмента вокруг центра с заданным радиусом.
4. Проверьте правильность установки радиуса, измерив его длину снова. Убедитесь, что радиус соответствует требуемым размерам и точности, чтобы гарантировать правильное построение шестиугольника вокруг данной окружности.
После того, как радиус окружности установлен, можно переходить к созданию шестиугольника вокруг этой окружности.
Определение центра окружности

Как определить центр окружности? Существует несколько методов:
- Метод хорд - выбирается хорда окружности и находится ее середина. В точке, которая является серединой хорды, проводятся перпендикуляры к этой хорде. Точка пересечения перпендикуляров будет являться центром окружности.
- Метод радиусов - выбирается две разные точки на окружности и соединяются отрезком. В точках пересечения радиусов (возможно, придется провести больше одной пары радиусов) рисуется прямая. Прямая будет пересекать окружность в точке, которая будет являться ее центром.
- Метод пересечения дуг - выбираются три точки на окружности и соединяются они по порядку от первой до третьей. Проводятся перпендикуляры через середины двух отрезков, образованных дугами. Точка пересечения перпендикуляров будет являться центром окружности.
После определения центра окружности, можно приступать к построению шестиугольника. Центр окружности будет одной из вершин шестиугольника, а его радиус будет одним из отрезков, соединяющих центр с вершиной шестиугольника. Остальные вершины шестиугольника можно найти, используя геометрическую конструкцию.
Расчет внешней длины стороны шестиугольника
Для расчета внешней длины стороны шестиугольника необходимо знать радиус описанной окружности. Радиус описанной окружности представляет собой расстояние от центра окружности до любой из вершин шестиугольника.
Формула для расчета внешней длины стороны шестиугольника, используя радиус описанной окружности R, следующая:
- Умножить радиус описанной окружности на 2, чтобы получить диаметр.
- Умножить диаметр на √3 (квадратный корень из 3), чтобы найти внешнюю длину стороны шестиугольника.
Формула внешней длины стороны шестиугольника: S = 2R√3, где S - внешняя длина стороны шестиугольника, R - радиус описанной окружности.
Например, если радиус описанной окружности равен 5 см, то:
- Диаметр окружности: 2 * 5 = 10 см.
- Внешняя длина стороны шестиугольника: 10 * √3 ≈ 17,32 см.
Таким образом, внешняя длина стороны шестиугольника с радиусом описанной окружности 5 см составляет примерно 17,32 см.
Построение вершин шестиугольника
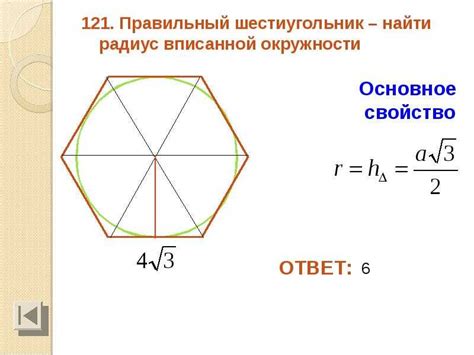
Построение вершин шестиугольника вокруг окружности требует тщательного расчета и точных измерений.
Для начала необходимо определить центр окружности и ее радиус. Затем следует провести оси симметрии окружности, которые пересекаются в центре и проходят через точки пересечения окружности с ее основанием.
Далее, чтобы найти вершины шестиугольника, нужно разделить окружность на шесть равных угловых секторов. Один из способов это сделать - взять ось симметрии и провести две линии, составляющие угол в 60 градусов с этой осью.
Полученные точки пересечения окружности и линий будут являться вершинами шестиугольника. Важно помнить, что шестиугольник можно построить внутрь или вокруг окружности, в зависимости от выбранного метода.
Для повышения точности построения рекомендуется использовать геометрические инструменты, такие как циркуль, линейку и угольник. Также следует учесть, что конечный результат может зависеть от точности измерений и выполнения построительных шагов.
Для аппроксимации шестиугольника можно использовать методы интерполяции, когда с помощью линий и измерений строятся точки-промежуточные, которые затем связываются и образуют фигуру, близкую к идеальному шестиугольнику.
Важно отметить, что построение вершин шестиугольника является лишь одним из этапов в создании данной фигуры. Все остальные стороны и углы также должны быть построены и проверены для получения правильного шестиугольника.
Соединение вершин шестиугольника
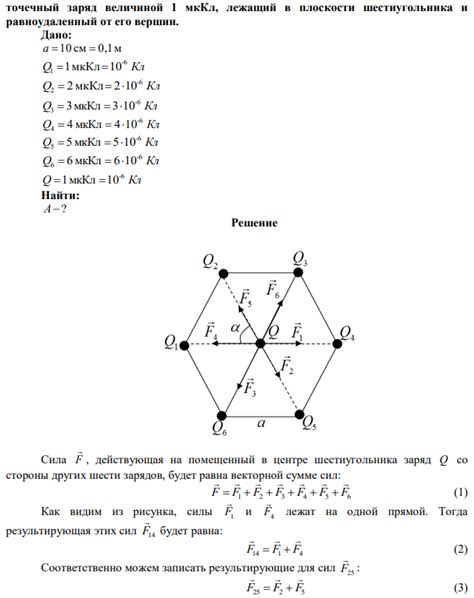
Построение шестиугольника вокруг окружности предполагает соединение вершин этого фигурой для образования полной геометрической фигуры. Для этого необходимо соединить шесть вершин шестиугольника под определенным углом друг к другу.
Для начала выберем одну из вершин шестиугольника. От нее проведем лучи, которые будут являться сторонами шестиугольника. Подходящим углом для проведения лучей будет 60 градусов, поскольку каждый внутренний угол шестиугольника равен 120 градусам.
Проведя лучи от выбранной вершины, пометим точки пересечения с окружностью. Соединим эти точки последовательно между собой, чтобы получить шестиугольник.
Таким образом, повторяя этот процесс для каждой вершины, мы соединим все вершины шестиугольника и получим готовую фигуру вокруг окружности.
Готовый шестиугольник вокруг окружности
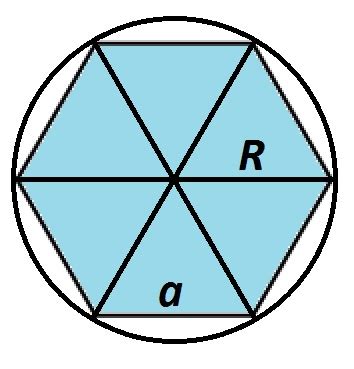
Чтобы построить шестиугольник вокруг окружности, вам понадобятся всего два инструмента: циркуль и линейка. Сначала проведите окружность с центром в заданной точке. Затем, используя линейку, соедините каждую вершину окружности с центром.
Вот как выглядит готовый шестиугольник вокруг окружности:
Геометрическое свойство:
У шестиугольника все стороны и углы равны между собой. Этот факт делает его особенно интересным для геометров и математиков. Внешний вид шестиугольника напоминает пчелиный улей или соты, что делает его еще более уникальным и привлекательным для наблюдения.
Примеры использования:
Готовый шестиугольник вокруг окружности может использоваться в архитектуре, дизайне и искусстве. Его симметричная форма придает проекту эстетическую гармонию и привлекательность.
Также шестиугольник вокруг окружности может служить основой для создания подробной геометрической конструкции или сложной модели.