Корреляция – это статистическая зависимость между двумя или более переменными. Анализ корреляции позволяет определить, насколько сильно связаны между собой различные характеристики или факторы. Для строительства таблицы корреляции необходимо знание основных принципов и последовательности шагов. В этой статье мы рассмотрим главные способы построения таблицы корреляции, которые помогут вам получить полные и надежные результаты.

Шаг 1: Сбор данных. Прежде чем построить таблицу корреляции, необходимо собрать достаточное количество данных, связанных с переменными, которые вы планируете исследовать. Например, если вы хотите изучить влияние факторов, таких как возраст, доход и образование, на уровень счастья, вам понадобится информация о каждом из этих факторов для каждого человека в вашей выборке.

Шаг 2: Вычисление корреляции. После того, как у вас есть данные, вы можете приступить к вычислению коэффициентов корреляции. Существует несколько различных методов вычисления, таких как корреляция Пирсона, Спирмена и Кендалла. Каждый из методов имеет свои преимущества и подходит для разных типов данных. Выбор метода зависит от конкретной задачи и типа данных, которые вы исследуете.

Шаг 3: Построение таблицы корреляции. Когда вы закончите вычисления, можно перейти к построению таблицы корреляции. Таблица корреляции представляет собой двумерную матрицу, в которой каждой паре переменных соответствует коэффициент корреляции. Обычно таблицу корреляции представляют с помощью чисел, расположенных в виде матрицы или с помощью графиков, таких как диаграмма рассеяния или тепловая карта.

Определение корреляции и ее значение

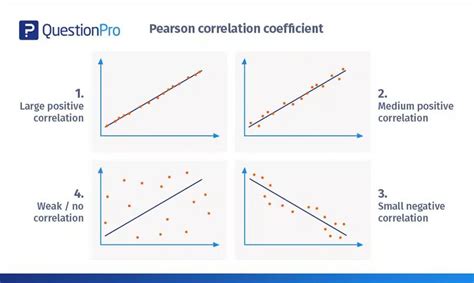
Значение корреляции указывает на наличие или отсутствие взаимосвязи между переменными. Если корреляция близка к 1, то это говорит о сильной положительной связи, то есть при увеличении значений одной переменной значения другой переменной также увеличиваются. Если корреляция близка к -1, то это указывает на сильную отрицательную связь, где при увеличении значений одной переменной значения другой переменной уменьшаются. Корреляция, близкая к 0, говорит о слабой или отсутствующей связи между переменными.

Значимость корреляции рассчитывается с помощью статистического тестирования и обычно выражается в виде p-значения. Малое p-значение указывает на то, что корреляция является статистически значимой, то есть вероятность случайной связи между переменными крайне низка.

Оценка корреляции и ее значения имеют важное значение в многих областях, включая науку, экономику, медицину, социологию и другие. Знание о связи между переменными позволяет прогнозировать и анализировать данные, что является важным инструментом в принятии решений и выявлении закономерностей.

Понятие корреляции и ее роль в анализе данных

Корреляция особенно полезна в анализе данных, так как позволяет определить, есть ли существенная связь между двумя переменными, что может помочь в прогнозировании их будущего поведения или взаимодействия. Например, корреляция может показать, насколько сильно уровень образования влияет на заработную плату, или насколько погодные условия влияют на продажи определенного товара.

Таблица корреляции является инструментом, который позволяет визуализировать корреляционные связи между переменными. Она представляет собой матрицу, в которой переменные представлены в строках и столбцах, а коэффициенты корреляции отражаются в ячейках. Коэффициент корреляции может принимать значения от -1 до 1. Если коэффициент близок к 1, это указывает на сильную положительную связь между переменными, а если близок к -1, это указывает на сильную отрицательную связь. Коэффициент близок к 0, если связи между переменными нет.

Для построения таблицы корреляции, необходимо выполнить следующие шаги:

1. Собрать данные, которые требуется проанализировать.
2. Определить переменные, которые будут анализироваться.
3. Вычислить коэффициенты корреляции между всеми парами переменных с использованием соответствующих статистических методов.
4. Построить матрицу, в которой значения коэффициентов корреляции отображаются в соответствующих ячейках.

Таблица корреляции и ее анализ помогают исследователям и аналитикам лучше понять данные и выявить тенденции, которые могут быть полезными для различных областей, включая маркетинг, экономику, социологию и многие другие. Умение строить и интерпретировать таблицы корреляции является важным инструментом в анализе данных и помогает принимать основанные на фактах решения.

Принципы построения таблицы корреляции

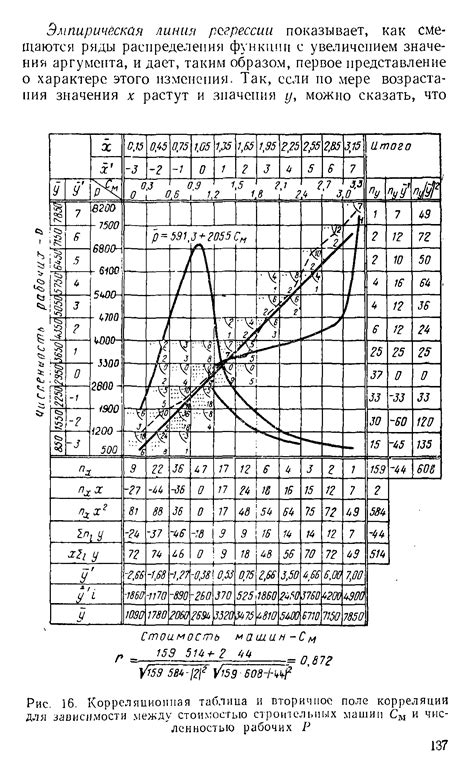
1. Определение переменных:

Первый шаг в построении таблицы корреляции – это определение переменных, которые будут включены в анализ. Важно выбрать переменные, которые должны иметь какую-то логическую связь между собой.

2. Очистка данных:

Прежде чем приступить к построению таблицы корреляции, необходимо провести очистку данных от ошибок, пропусков и выбросов. Это поможет получить более достоверные результаты и исключит искажения в анализе.

3. Выбор метода расчета:

Существует несколько методов расчета корреляции, таких как коэффициент Пирсона, коэффициент Спирмена и коэффициент Кендалла. Важно выбрать подходящий метод в зависимости от типа данных и цели исследования.

4. Создание таблицы:

После выбора метода расчета можно приступить к созданию таблицы корреляции. Для этого используется тег <table>. В верхней строке таблицы указываются названия переменных, а в остальных строках – значения коэффициентов корреляции.

5. Визуализация результатов:

Для удобства анализа рекомендуется визуализировать результаты таблицы корреляции. Например, можно использовать цветовую шкалу или график, чтобы наглядно отобразить силу и направление взаимосвязей между переменными.

Выбор метода коэффициента корреляции

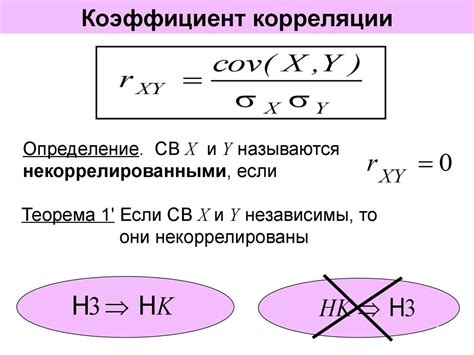
Одним из наиболее популярных методов является Пирсона, или линейный коэффициент корреляции. Он применяется для измерения линейной взаимосвязи между двумя непрерывными переменными. Если исследуемые переменные могут быть описаны линейной зависимостью, то Пирсон будет правильным выбором.

Если данные являются ранговыми или не соответствуют требованиям для применения Пирсона, рекомендуется использовать Спирмена или Кендалла, соответственно. Спирмена - метод непараметрической корреляции, который позволяет оценить монотонную взаимосвязь между переменными. Кендалла - также непараметрический коэффициент, предназначенный для измерения зависимости между переменными, особым образом учитывающий их ранжировку.

Кроме этого, существуют и другие методы коэффициента корреляции, такие как точечного бисериального, полифинного и другие, которые применяются в зависимости от специфики исследования и характера данных.

Выбор метода коэффициента корреляции требует разумного рассмотрения особенностей исследуемых данных и явления. Важно выбрать подходящий метод, чтобы получить более точные и интерпретируемые результаты.

Учет ограничений и особенностей данных

При построении таблицы корреляции необходимо учитывать ограничения и особенности данных. Это позволит достичь более точных и надежных результатов анализа.

Во-первых, необходимо учесть тип данных, которые анализируются. Корреляционный анализ может быть применен к различным типам данных, включая числовые, категориальные и бинарные переменные. В зависимости от типа данных будут использоваться различные методы и метрики корреляции.

Во-вторых, следует проверить данные на наличие пропущенных значений. Пропущенные значения могут повлиять на результаты анализа и искажать полученные корреляционные коэффициенты. Поэтому необходимо предварительно заполнить пропущенные значения или исключить строки с пропусками.

Другим важным аспектом является наличие выбросов или аномальных значений в данных. Они могут значительно искажать результаты корреляционного анализа. Поэтому перед построением таблицы корреляции рекомендуется провести анализ выбросов и принять соответствующие меры: исключить выбросы или использовать методы робастного корреляционного анализа.

Также стоит обратить внимание на линейность связи между переменными. Корреляционный анализ основан на предположении о линейной связи между переменными. Если связь является нелинейной, результаты корреляционного анализа могут быть неправильными. В таких случаях можно применить специальные методы нелинейной корреляции или преобразовать переменные для приближения к линейной связи.

Наконец, необходимо учитывать размер выборки. Корреляционные коэффициенты могут быть ненадежными при малом объеме выборки. Поэтому перед проведением корреляционного анализа следует убедиться в достаточной численности выборки и, при необходимости, использовать методы для оценки статистической значимости корреляции.

Все эти ограничения и особенности данных необходимо учитывать при построении таблицы корреляции, чтобы получить правильные и интерпретируемые результаты анализа.

Шаги построения таблицы корреляции

Для построения таблицы корреляции следуйте нижеприведенным шагам:

1. Определите переменные: Выберите переменные, которые вы хотите исследовать и измеряйте их значения для каждого наблюдения.
2. Подготовьте данные: Обработайте данные, убрав выбросы и пропущенные значения, если таковые имеются. Убедитесь, что все переменные числовые или можно их преобразовать в числовой вид.
3. Вычислите коэффициенты корреляции: Рассчитайте коэффициенты корреляции для всех пар переменных, которые вы хотите сравнить. Используйте подходящий метод, такой как коэффициент Пирсона или Спирмена, в зависимости от типа данных и распределения переменных.
4. Постройте таблицу корреляции: Создайте таблицу, где каждая ячейка представляет соответствующий коэффициент корреляции между двумя переменными. Заполните таблицу, включив значения коэффициентов и их статистическую значимость, если это применимо.
5. Интерпретируйте результаты: Проанализируйте таблицу корреляции, чтобы определить характер и силу связи между переменными. Обратите внимание на значимые коэффициенты корреляции и их направление (положительное или отрицательное).

Обратите внимание, что таблица корреляции не дает причинно-следственных связей между переменными, а лишь показывает, насколько они связаны между собой.

Сбор и подготовка данных

Для построения таблицы корреляции необходимо собрать и подготовить данные, чтобы они были готовы для анализа. В данном разделе мы будем рассматривать принципы и шаги сбора и подготовки данных перед построением таблицы корреляции.

1. Определение цели исследования: перед началом сбора данных необходимо определить цель исследования. Четкое определение цели поможет вам сфокусироваться на необходимых данных и избежать ненужных затрат.
2. Выбор источников данных: определите, откуда вы будете получать данные. Это может быть различные базы данных, опросы, архивы и другие источники.
3. Создание плана сбора данных: разработайте план сбора данных, который определит, какие переменные нужно измерить, какие методы сбора данных использовать и какой объем данных нужен.
4. Сбор данных: приступите к сбору данных в соответствии с разработанным планом. Важно обеспечить точность и непрерывность сбора данных, чтобы избежать искажений результатов.
5. Очистка и проверка данных: проведите проверку данных на ошибки, пропуски и несоответствия. Удалите или исправьте ошибочные значения и пропуски, чтобы получить надежные данные.
6. Преобразование данных: в некоторых случаях может потребоваться преобразование данных перед анализом. Например, это может быть масштабирование данных или преобразование категориальных переменных в числовые.

После завершения этих этапов сбора и подготовки данных, вы получите надежные и готовые для анализа данные, которые могут быть использованы для построения таблицы корреляции и других статистических анализов.