Как построить треугольник из отрезков — правила и условия

Построение треугольника – это одна из основных задач геометрии. Здесь требуется провести отрезки, которые соединяют три точки на плоскости, таким образом, чтобы они образовывали треугольник. Но как правильно построить треугольник? В данной статье мы рассмотрим основные правила и условия, которые необходимо учесть при выполнении этой задачи.

Вначале следует уяснить, что для построения треугольника необходимо иметь три отрезка различной длины. При этом эти отрезки должны удовлетворять некоторым условиям. Во-первых, сумма длин двух отрезков всегда должна превышать длину третьего отрезка: a + b > c, a + c > b, b + c > a. В противном случае треугольник невозможно построить.

Во-вторых, длина любого отрезка не может быть равна нулю или отрицательному значению. Данное условие связано с геометрическим смыслом треугольника – это фигура, состоящая из трех отрезков, которые образуют замкнутую фигуру с ненулевой площадью.

Также стоит отметить, что длина каждого отрезка должна быть меньше суммы длин двух остальных отрезков. В противном случае треугольник получится вырожденным – это будет прямая линия или точка, а не фигура с тремя сторонами.

Правила и условия построения треугольника из отрезков

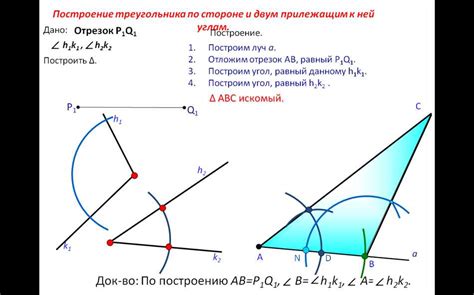
Основные правила построения треугольника из отрезков:

1. Длины всех трех отрезков должны быть положительными числами: a > 0, b > 0, c > 0.
2. Сумма длин двух сторон треугольника должна быть больше третьей стороны:

   a + b > c
   b + c > a
   a + c > b

Условия построения треугольника из отрезков:

1. Треугольник двусторонний – у него есть две одинаковые стороны. В этом случае, чтобы получить треугольник, достаточно, чтобы сумма длин двух сторон была больше третьей:

   a + b > c

2. Треугольник равносторонний – все стороны треугольника равны. В этом случае все три условия должны выполняться:

   a + b > c
   b + c > a
   a + c > b

3. Треугольник разносторонний – у него все три стороны разные. В этом случае также все три условия должны выполняться:

   a + b > c
   b + c > a
   a + c > b

Следуя правилам и условиям, можно построить треугольник из отрезков и узнать его тип: равносторонний, разносторонний или двусторонний. Построенный треугольник может быть использован для решения разных задач геометрии и математики.

Условие построения треугольника

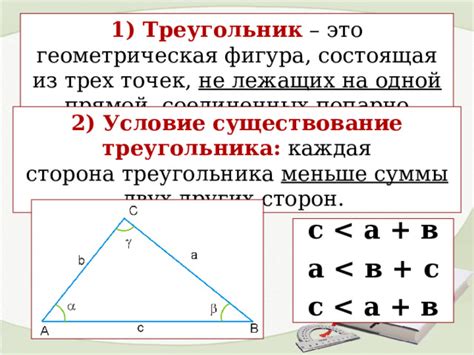
Для построения треугольника из отрезков необходимо соблюдать следующие условия:

• Сумма длин любых двух отрезков должна быть больше длины третьего отрезка. То есть, для отрезков АВ, ВС и CD, должны выполняться следующие условия: AB + BC > AC, AC + CD > AD, AB + CD > AD.
• Отрезки не могут быть отрицательными или равными нулю.

Если данные условия не выполняются, то треугольник не может быть построен из данных отрезков.

Правила построения треугольника

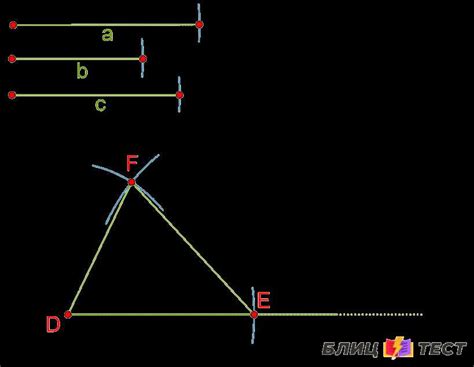
1. Неравенство треугольника:

Сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Иными словами, если a, b и c - длины сторон треугольника, то должны выполняться следующие неравенства:

a + b > c

b + c > a

c + a > b

2. Угловая сумма треугольника:

Сумма значений углов треугольника всегда равна 180 градусов. То есть, если α, β и γ - углы треугольника, то:

α + β + γ = 180°

3. Высота в треугольнике:

Высота треугольника – это отрезок, проведенный из одного из вершин треугольника к основанию, перпендикулярно основанию. Высота делит треугольник на два подобных между собой треугольника.

Примечание: для описания данных правил использованы понятия и термины, используемые в геометрии. Знание этих правил и понятий позволяет более точно и строго определить, какие отрезки могут быть частью треугольника и в каком случае определенный набор отрезков не может образовывать треугольник.