Треугольник – это многоугольник с тремя сторонами и тремя углами. Построение треугольника с заданными сторонами и высотой может быть сложной задачей, однако с помощью этого руководства вы сможете справиться с ней без особых проблем. В этой статье мы рассмотрим различные методы и инструкции, которые помогут вам построить треугольник с заданными характеристиками.

Первый шаг в построении треугольника с заданными сторонами и высотой – определить вид треугольника, который вы хотите построить. Треугольники могут быть различными: равносторонними, равнобедренными или разносторонними. Каждый из этих видов треугольников имеет свои особенности и требует определенных действий для построения.

Следующий шаг – определить значения сторон и высоты треугольника. Для этого вам потребуется измерительная лента или линейка. Измерьте каждую сторону треугольника и высоту от выбранной стороны до противоположного угла. Запишите эти значения, они будут использоваться в дальнейшем.

Треугольник с заданными сторонами и высотой - руководство и инструкция

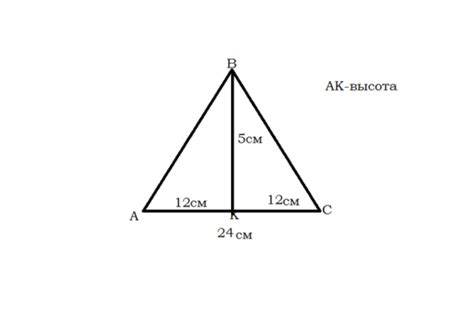
Вот пошаговая инструкция о том, как построить треугольник с заданными сторонами и высотой:

1. Задайте длины сторон треугольника, которые должны быть положительными числами. Назовите их а, b и с. Убедитесь, что условие неравенства треугольника выполняется: сумма двух сторон должна быть больше третьей стороны.
2. Вычислите площадь треугольника, используя формулу S = (a * h) / 2, где S - площадь, a - одна из сторон, h - высота, соответствующая этой стороне.
3. Найдите неизвестную высоту h, используя формулу h = (2 * S) / a, где h - высота, S - площадь, a - сторона, к которой относится данная высота.
4. Постройте первую сторону треугольника, используя отрезок длиной a. Установите одну из вершин этого отрезка в точку (0, 0).
5. Постройте вторую сторону треугольника, используя отрезок длиной b. Отложите от вершины первой стороны отрезок длиной b и соедините эту точку с началом первой стороны.
6. Постройте третью сторону треугольника, используя отрезок длиной c. Отложите от вершины второй стороны отрезок длиной c и соедините эту точку с началом второй стороны.
7. Треугольник с заданными сторонами и высотой построен! Проверьте его размеры и форму для удостоверения корректности.

Надеемся, что эта инструкция поможет вам построить треугольник с заданными сторонами и высотой без особых сложностей. Удачи!

Определение треугольника и его свойства

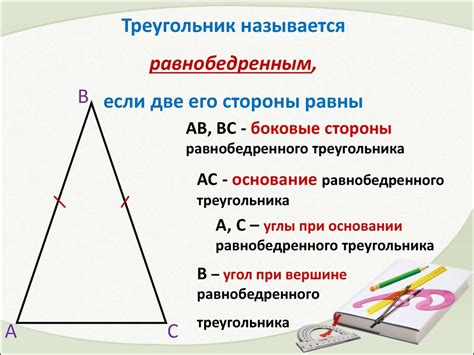
Основные свойства треугольника:

• Сумма всех углов треугольника равна 180 градусам. Это свойство называется "сумма углов треугольника".
• Наибольшая сторона треугольника всегда меньше суммы двух остальных сторон. Это свойство называется "неравенство треугольника".
• Треугольник может быть разделен на два более маленьких треугольника при помощи одной из его сторон, называемой "биссектрисой".
• Высота треугольника - это перпендикуляр, проведенный из вершины треугольника к противоположной стороне. Высоты пересекаются в одной точке, называемой "точкой пересечения высот треугольника".

Знание этих свойств поможет в построении треугольника с заданными сторонами и высотой.

Изучение заданных сторон треугольника

Перед тем как приступить к построению треугольника, необходимо изучить заданные стороны. Знание длин сторон позволяет правильно определить длину высоты и построить треугольник с требуемыми характеристиками.

Изучение заданных сторон можно начать с определения типа треугольника. Заданные стороны могут образовывать разные типы треугольников: равнобедренный, разносторонний или равносторонний. Для этого необходимо сравнить длины сторон и выявить совпадения.

Если все три стороны имеют одинаковую длину, то треугольник является равносторонним. Если две стороны имеют одинаковую длину, то треугольник является равнобедренным. Если все три стороны имеют различные длины, то треугольник является разносторонним.

После определения типа треугольника можно приступать к вычислению высоты. Для этого используется формула, которая может быть различной в зависимости от известных данных о треугольнике. Высота может быть найдена с помощью формулы Герона, формулы для равнобедренного треугольника или формулы для равностороннего треугольника.

Если известны все три стороны треугольника, то высота может быть найдена с помощью формулы Герона:

hu = 2 * S / a,
где hu - высота треугольника,
S - площадь треугольника,
a - длина стороны треугольника.

Если известны длина основания и высота в равнобедренном треугольнике, то высота может быть найдена по формуле:

hu = 2 * S / b,
где hu - высота треугольника,
S - площадь треугольника,
b - длина основания треугольника.

Если треугольник является равносторонним, то высота может быть найдена по формуле:

hu = a * sqrt(3) / 2,
где hu - высота треугольника,
a - длина стороны треугольника.

После вычисления длины высоты можно приступать к построению треугольника с заданными сторонами и высотой. Воспользуйтесь соответствующими инструкциями и руководством для правильного построения.

Расчет площади треугольника по заданным сторонам и высоте

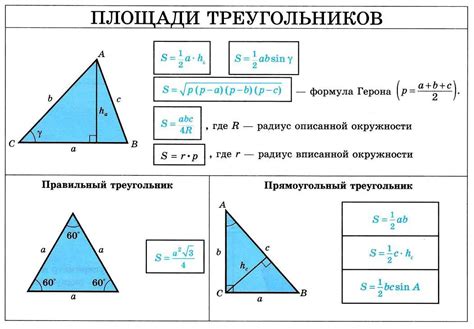
Для расчета площади треугольника по заданным сторонам и высоте можно использовать формулу:

S = (a * h) / 2

где S - площадь треугольника, a - длина одной из сторон треугольника, h - высота, опущенная на эту сторону.

Для начала, нужно измерить длины сторон треугольника и высоту, опущенную на одну из этих сторон.

Затем, подставляя значения в формулу, можно вычислить площадь треугольника.

Важно помнить, что все значения должны быть указаны в одной единице измерения, например, в сантиметрах или в метрах.

Помимо этого, необходимо убедиться, что заданные стороны и высота соответствуют правилам построения треугольника. Например, сумма длин двух сторон всегда должна быть больше длины третьей стороны.

Расчет площади треугольника по заданным сторонам и высоте позволяет определить его площадь без необходимости знать значения углов или других сторон. Это может быть полезно в различных задачах, связанных с геометрией или строительством.

Построение треугольника на плоскости с использованием заданных сторон и высоты

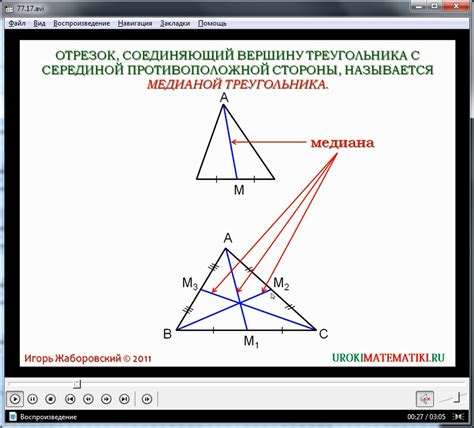
Для построения треугольника с использованием заданных сторон и высоты, следуйте следующим шагам:

1. Шаг 1: Начните с маркировки точки A на плоскости, которая будет соответствовать одной из вершин треугольника.
2. Шаг 2: Используя линейку и компас, отметьте от точки A отрезок AB, который будет соответствовать одной из сторон треугольника длиной, заданной в условии.
3. Шаг 3: Из точки B проведите перпендикуляр к стороне AB, который будет пересекать сторону AB в точке C и будет соответствовать высоте треугольника.
4. Шаг 4: Соедините точки A и C линией, чтобы получить одну из сторон треугольника.
5. Шаг 5: Из точек B и C проведите линии, соединяющие их с точкой A, чтобы получить оставшиеся стороны треугольника.
6. Шаг 6: Убедитесь, что все стороны треугольника соответствуют заданным значениям, а высота перпендикулярна одной из сторон.

Это метод позволяет построить треугольник с заданными сторонами и высотой на плоскости. Он основан на геометрических принципах и может быть использован для решения различных задач в геометрии.

Основные шаги построения треугольника

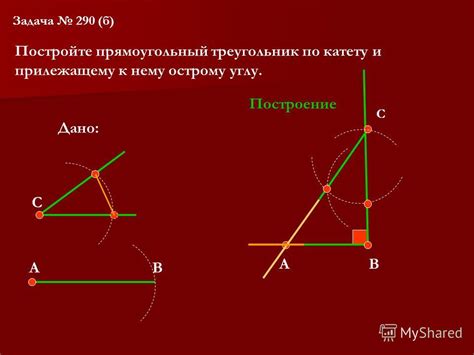
Для построения треугольника с заданными сторонами и высотой необходимо выполнить следующие шаги:

1. Шаг 1: Найдите длины сторон треугольника и заданную высоту. Запишите эти значения.
2. Шаг 2: Используя линейку и карандаш, на листе бумаги отметьте точку A, которая будет вершиной треугольника.
3. Шаг 3: От точки A отложите отрезок BC, равный заданной длине стороны AB треугольника. Соедините точки B и C линией.
4. Шаг 4: Из точки A проведите отрезок AD перпендикулярно стороне BC. Длина этого отрезка должна равняться заданной высоте треугольника.
5. Шаг 5: Соедините точки D, B и C линиями. Полученная фигура будет являться треугольником с заданными сторонами и высотой.

Запомните, что построение треугольника с заданными сторонами и высотой является графическим методом и можно использовать только простые инструменты, как линейка и карандаш.

Удачи вам в создании треугольника!

Проверка согласования построения треугольника с заданными параметрами

После того, как вы построите треугольник с заданными сторонами и высотой, рекомендуется проверить, соответствует ли фактический треугольник заданным параметрам.

Первым шагом является измерение сторон треугольника с помощью линейки или другого измерительного инструмента. Запишите полученные значения для каждой стороны.

Далее измерьте высоту треугольника, опирающуюся на одну из сторон. Если у вас есть возможность, используйте уровень или другой инструмент для определения точности измерений высоты.

Сравните измеренные значения сторон с заданными значениями. Если они близки и расхождения незначительны, то ваш треугольник соответствует заданным параметрам.

Однако, если измеренные значения сильно отличаются от заданных, возможно, вы допустили ошибку при построении треугольника или использовали неправильные значения сторон и высоты. В этом случае рекомендуется перепроверить соответствующую математическую формулу для построения треугольника, а также удостовериться в правильности измерений.

Правильное построение треугольника с заданными параметрами гарантирует его геометрическую точность и соответствие требуемым спецификациям.

Дополнительные сведения о треугольниках с заданными сторонами и высотой

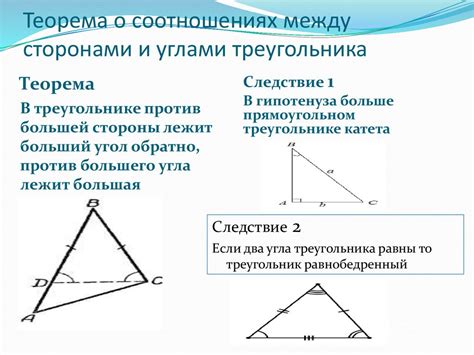
При построении треугольника с заданными сторонами и высотой необходимо учитывать несколько факторов. Прежде всего, треугольник может быть построен только если сумма длин любых двух сторон больше третьей стороны.

Кроме того, высота треугольника определяется как перпендикуляр, проведенный из вершины треугольника к противолежащей стороне. Высота делит треугольник на два равных пополам.

Если известны длины всех трех сторон треугольника и его высота, то можно использовать различные формулы для рассчета других характеристик треугольника, например, площади или углов.

Формула для расчета площади треугольника:

Площадь = (основание * высота) / 2

Основание треугольника - это любая из его сторон, к которой проведена высота.

Формула для расчета углов треугольника:

Угол A = arccos((b^2 + c^2 - a^2) / (2 * b * c))

Угол B = arccos((a^2 + c^2 - b^2) / (2 * a * c))

Угол C = arccos((a^2 + b^2 - c^2) / (2 * a * b))

Где a, b и c - длины сторон треугольника.

Используя эти формулы, вы можете получить дополнительные сведения о треугольнике с заданными сторонами и высотой, такие как его площадь и углы. Эти сведения помогут вам более детально изучить и описать треугольник, а также решить задачи, связанные с его геометрическими свойствами.

Рекомендации по измерению сторон треугольника и высоты

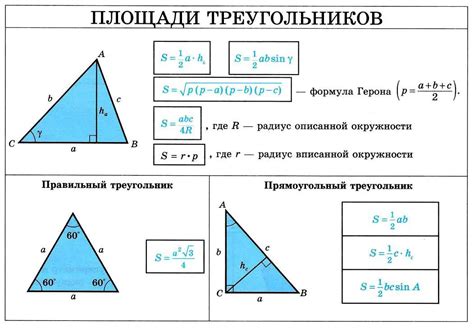
1. Измерение сторон треугольника:

• Используйте линейку или мерную ленту для измерения каждой стороны треугольника.
• Приложите линейку или мерную ленту к началу одной из сторон и проведите ее по всей длине стороны.
• Убедитесь, что линейка или мерная лента плотно прилегает к стороне треугольника, чтобы измерение было точным.
• Запишите измерения каждой стороны треугольника и удостоверьтесь, что они являются положительными числами.

• Измерьте расстояние от вершины треугольника до основания, которое является перпендикулярным отрезком, проведенным из вершины к противоположной стороне.
• Приложите линейку или мерную ленту к вершине треугольника и опустите ее до основания, параллельно противоположной стороне.
• Убедитесь, что линейка или мерная лента плотно прилегает к треугольнику и перпендикулярно проведенному отрезку.
• Запишите измерение высоты треугольника и удостоверьтесь, что оно является положительным числом.

Тщательное измерение сторон треугольника и высоты помогает гарантировать точность и корректность построения треугольника с заданными параметрами. Не забывайте следовать указанным рекомендациям и проверять значения измерений перед построением треугольника.