Углы 30 градусов – одни из самых распространенных углов, которые приходится строить в геометрии. Они используются для построения треугольников, параллелограммов и многих других фигур. Однако, не всегда углы 30 градусов легко построить без подходящих инструментов. В этой статье мы рассмотрим способ построения углов 30 градусов с помощью циркуля и линейки.
Циркуль – это инструмент, который используется для построения окружностей и различных геометрических фигур. Для построения угла 30 градусов нам понадобятся два циркуля и линейка. Сначала мы нарисуем прямую линию, которая будет служить одной из сторон угла. Затем установим один циркуль в точку начала линии и нарисуем окружность.
Линейка – это прямой инструмент, который используется для измерения и рисования прямых линий. Чтобы построить угол 30 градусов, нам понадобится также линейка для определения точки пересечения прямой линии и окружности. Затем мы установим второй циркуль в эту точку и проведем дугу, которая будет пересекать окружность.
Инструменты для построения углов

Для построения углов с углом 30 градусов с помощью циркуля и линейки вам понадобятся следующие инструменты:
- Циркуль: основной инструмент для рисования окружностей и дуг.
- Линейка: помогает провести прямые линии и измерить расстояние между точками.
- Карандаш: используется для отметки точек и проведения линий.
- Ластик: позволяет стирать ненужные отметки и обозначения.
Совместное использование циркуля и линейки позволяет строить углы различной величины с высокой точностью, в том числе углы 30 градусов.
Для построения угла в 30 градусов можно использовать следующий метод:
- С помощью линейки нарисуйте прямую линию AB.
- Установите центр циркуля в точку A и нарисуйте дугу, которая пересекает линию AB в точке C.
- Установите центр циркуля в точку C и нарисуйте дугу, которая пересекает предыдущую дугу в точке D.
- Проведите прямую линию CD.
Теперь у вас есть угол в 30 градусов, образованный линиями AB и CD.
Важно помнить, что для получения точного угла необходимо быть внимательным при проведении линий и настройке циркуля.
Что такое циркуль и линейка

Линейка – это измерительный инструмент, который используется для измерения длины и проведения прямых линий. Линейку можно найти в разных исполнениях: от обычной деревянной до металлической с делениями в миллиметрах. Она имеет градуировку, которая помогает определить длину объекта или расстояние между двумя точками.
Циркуль и линейка являются основными инструментами в геометрии и строительстве. С их помощью можно строить разнообразные геометрические фигуры и решать задачи на нахождение углов, расстояний и площадей.
Примечание: для построения углов 30 градусов с помощью циркуля и линейки используется техника деления угла пополам и построения равностороннего треугольника, что будет рассмотрено в дальнейших разделах статьи.
Как использовать циркуль и линейку
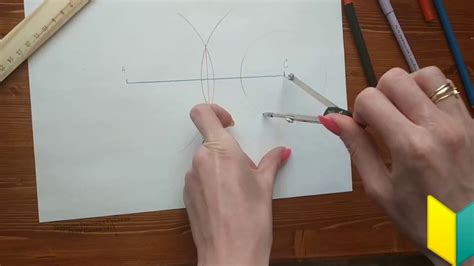
1. Разметка - перед началом работы необходимо провести разметку на листе бумаги. Разметка позволяет определить точные размеры и положение фигур на чертеже. Используйте линейку для проведения прямых линий и циркуль для построения окружностей и дуг.
2. Использование линейки - линейка помогает проводить прямые линии и измерять расстояния. Для проведения прямых линий, поместите линейку на бумаге так, чтобы ребро совпадало с носовым краем. Затем, с помощью карандаша или ручки, проведите линию вдоль края линейки.
3. Использование циркуля - циркуль позволяет рисовать окружности и дуги. Чтобы использовать циркуль, закрепите его на листе бумаги и установите нужный радиус. Затем, вращая ручку циркуля, проведите окружность или дугу.
4. Точность - при работе с циркулем и линейкой очень важно быть точным. Необходимо соблюдать все меры предосторожности, чтобы избежать погрешностей и неправильных результатов. Помните, что точное измерение и построение фигур является ключевым аспектом работы с циркулем и линейкой.
5. Практика - чтобы стать мастером в использовании циркуля и линейки, необходимо много практиковаться. Упражнения помогут развить навыки работы с инструментами и повысить точность чертежей.
Использование циркуля и линейки - это важный навык для всех, кто интересуется геометрией, черчением и архитектурой. Следуя указанным выше принципам, вы сможете строить точные и красивые фигуры и чертежи, которые будут радовать глаз и пониманию важности точности при работе с геометрическими инструментами
Методы построения угла 30 градусов

Первый метод основан на делении угла 60 градусов. Для начала построим прямой угол с помощью линейки и циркуля. Затем найдем середину одной из его сторон и проведем линию, которая пересечет другую сторону под углом в 90 градусов. Эта линия разобьет прямой угол пополам на два равных угла по 45 градусов каждый. Теперь найдем середину одного из этих углов и проведем линию, которая пересечет другую сторону под углом в 90 градусов. Эта линия разобьет угол 45 градусов пополам на два равных угла по 22,5 градуса каждый. Теперь найдем середину одного из этих углов и проведем линию, которая пересечет другую сторону под углом в 90 градусов. Эта линия разобьет угол 22,5 градуса пополам на два равных угла по 11,25 градуса каждый. И, наконец, найдем середину одного из этих углов и проведем линию, которая пересечет другую сторону под углом в 90 градусов. Таким образом, мы получим угол 11,25 градуса, который можно удвоить, чтобы получить угол 22,5 градуса, и затем еще раз удвоить, чтобы получить угол 45 градусов. Из угла 45 градусов мы можем легко получить угол 30 градусов путем деления его на половину.
Второй метод основан на построении правильного шестиугольника. Для начала построим прямую линию с помощью линейки. Затем определим середину этой линии и построим окружность с центром в этой точке и радиусом, равным длине прямой линии. С помощью циркуля проведем маркеры на этой окружности через каждые 60 градусов. Затем соединим эти маркеры, чтобы получить правильный шестиугольник. Углы между соседними сторонами этого шестиугольника будут равными и составлять 120 градусов каждый. Выберем одну из его сторон, поделим ее на 4 равные части и соединим точку деления с центром окружности. Полученный угол будет составлять 30 градусов.
| Метод | Принцип |
|---|---|
| Метод деления угла 60 градусов | Последовательное деление углов пополам |
| Метод построения правильного шестиугольника | Создание правильного шестиугольника и деление одной из его сторон на четверть |
Метод деления угла
В простых случаях, углы можно построить с помощью циркуля и линейки, используя метод деления. Данный метод основан на построении угла в несколько этапов:
- Пусть дан угол АВС, который нужно разделить на два угла равных 30 градусов.
- Сначала прокладываем линейку через вершину угла В и проводим прямую, которая пересекает сторону АС в точке D.
- С помощью циркуля, ставим центр в точку D и не перемещая его, проводим дугу, которая пересечет прямую ВС в точке М.
- Теперь ставим центр циркуля в точку М и без перемещения секущей ноги, проводим дугу, которая пересечет прямую ВС в точке N.
- Точки M и N будут находится на одинаковом расстоянии от точки D, следовательно мы получили два угла, равных 30 градусов каждый.
Этот метод является одним из самых точных в построении требуемого угла и часто используется при работе с циркулем и линейкой. Следуя этим шагам, вы легко сможете построить углы 30 градусов.
Метод построения равностороннего треугольника
Для построения равностороннего треугольника с помощью циркуля и линейки нужно выполнить следующие шаги:
- Возьмите линейку и проведите отрезок AB.
- Установите концы линейки на точки A и B и откройте циркуль до точки A.
- Сделайте точку C на пересечении дуг данного радиуса.
- Соедините точки A и C линией, а затем соедините точки C и B линией.
Теперь у вас есть равносторонний треугольник ABC, у которого все стороны и углы равны 60 градусов.
Метод строительного плетения

Для начала, на линейке отметьте отрезок длиной в 1 единицу измерения. Затем, используя циркуль, проведите дугу радиусом равным этому отрезку. Эта дуга будет пересекать линейку в точке B.
Затем, установите циркуль на точку B, и найдите точку C на дуге, которая будет равноудалена от точки B.
Следующим шагом, установите циркуль на точку C и проведите дугу, которая будет пересекать линейку в точке D.
Наконец, соедините точки B и D линией. Угол BCD будет равным требуемому углу 30 градусов.
Таким образом, метод строительного плетения позволяет построить углы 30 градусов с использованием простых инструментов - циркуля и линейки.