Построение вписанной окружности в прямоугольный треугольник – одна из важных геометрических задач, которую можно решить без использования измерений. Это позволяет развить навыки аналитической геометрии и использовать логическое мышление. В этой статье мы рассмотрим шаги, необходимые для построения вписанной окружности в прямоугольный треугольник.

Прямоугольный треугольник имеет один прямой угол, что делает его особо интересным для анализа. Построение вписанной окружности требует нахождения ее центра – точки пересечения трех биссектрис треугольника. Биссектрисы – это прямые, которые делят углы треугольника пополам. Они встречаются в одном центре – центре вписанной окружности.

В процессе построения придется провести несколько прямых линий и найти точку пересечения, что требует аккуратности и точности в действиях. Однако, используя логическое мышление, вы сможете преодолеть эти сложности и получить красивую вписанную окружность в прямоугольный треугольник.

Вписанная окружность: основные понятия и определения

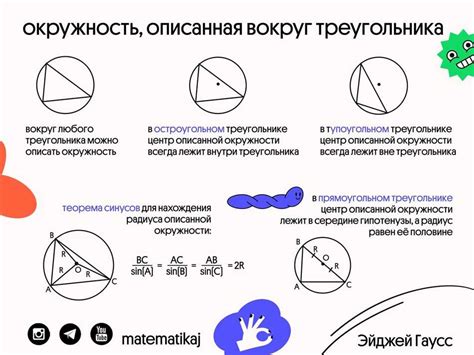
Рассмотрим прямоугольный треугольник, у которого один из углов является прямым (равен 90 градусам). Проведя биссектрису этого прямого угла, мы получим высоту треугольника, которая также является радиусом вписанной окружности. Биссектриса делит этот угол на два равных угла, а значит, также делит треугольник на два равных прямоугольных треугольника.

Если обозначить стороны треугольника как a, b и c, а радиус вписанной окружности как r, то можно выразить связь между этими величинами с помощью следующей формулы:

r = (a + b - c) / 2

Также, можно выразить радиус вписанной окружности через площадь треугольника (S) и его полупериметр (p), используя формулу:

r = S / p

Вписанная окружность имеет несколько важных свойств. Первое из них – каждая сторона треугольника является касательной к окружности и равна сумме двух отрезков, на которые она делит другие две стороны. Второе свойство заключается в том, что центр окружности является точкой пересечения биссектрис треугольника. И, наконец, третье свойство – радиус вписанной окружности всегда лежит внутри треугольника и является перпендикуляром к сторонам треугольника.

Расчеты и свойства вписанной окружности позволяют определить ее положение и размеры без необходимости проведения измерений сторон и углов треугольника.

Окружность, треугольник, расстояние от центра до сторон

Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу окружности. Радиус окружности можно выразить с помощью формулы:

r = abc / (4S),

где r - радиус окружности, a, b, c - длины сторон треугольника, S - площадь треугольника.

Таким образом, чтобы построить вписанную окружность в прямоугольный треугольник без измерений, необходимо найти площадь треугольника и длины его сторон. Затем, используя формулу, вычислить радиус окружности. С помощью полученного радиуса можно построить окружность, касающуюся всех сторон треугольника.

Существующие методы построения вписанной окружности в прямоугольный треугольник

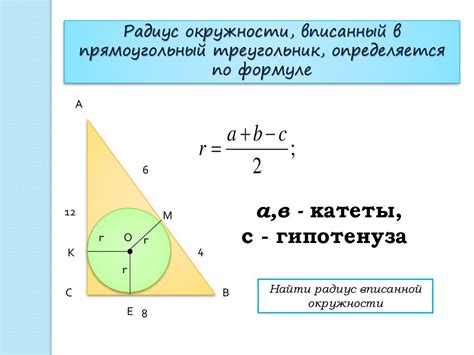
Существует несколько методов построения вписанной окружности в прямоугольный треугольник без использования каких-либо измерений. Они основаны на геометрических свойствах треугольника и прямых.

Один из таких методов - метод построения с использованием перпендикуляров. Для этого нужно провести перпендикуляры к сторонам прямоугольного треугольника из его вершин и найти точку их пересечения. Эта точка будет центром вписанной окружности.

Другой метод - метод построения с использованием биссектрисы угла. Для этого нужно найти биссектрису одного из углов прямоугольного треугольника и найти точку ее пересечения с противолежащей стороной. Эта точка также будет центром вписанной окружности.

Третий метод - метод построения с использованием высоты треугольника. Для этого нужно провести высоту треугольника из одной из его вершин. Затем нужно найти середину этой высоты и провести окружность с центром в этой точке и радиусом, равным половине длины высоты. Это будет вписанная окружность.

Каждый из этих методов имеет свои особенности и может быть полезен при решении конкретных задач. Выбор того или иного метода зависит от условий задачи и предпочтений самого конструктора.

Методы на основе полупериметра и радиуса

Существует несколько методов, которые позволяют построить вписанную окружность в прямоугольный треугольник без использования измерений. Один из таких методов основан на использовании полупериметра и радиуса вписанной окружности.

Для начала обозначим стороны прямоугольного треугольника: a, b и c, где a и b - катеты, а c - гипотенуза.

Полупериметр треугольника вычисляется по формуле: p = (a + b + c) / 2.

Радиус вписанной окружности можно найти с помощью следующей формулы: r = p - c.

Для построения вписанной окружности необходимо провести радиус r из середины гипотенузы c до точки касания окружности и треугольника.

Таким образом, используя метод на основе полупериметра и радиуса, можно построить вписанную окружность в прямоугольный треугольник без измерений.

Методы на основе длин сторон и радиуса

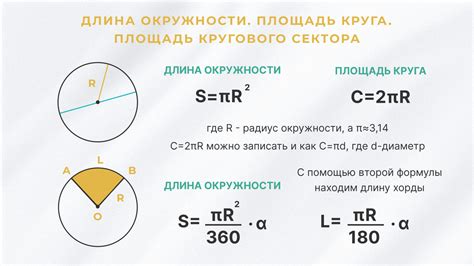
Существуют различные методы для построения вписанной окружности в прямоугольный треугольник без необходимости измерять его стороны и радиус. Рассмотрим некоторые из них:

1. Метод, основанный на длинах сторон треугольника:

Пусть a, b и c - стороны прямоугольного треугольника, а r - радиус его вписанной окружности.

Выражение для радиуса r можно найти по формуле r = (a + b - c) / 2, где a, b и c - длины сторон треугольника.

2. Метод, основанный на радиусе окружности и площади треугольника:

Если r - радиус вписанной окружности, а S - площадь треугольника, то выражение для радиуса r можно найти по формуле r = S / (a + b + c),

где a, b и c - длины сторон треугольника.

3. Метод, основанный на радиусе окружности и произведении длин сторон треугольника:

Если r - радиус вписанной окружности, а p - полупериметр треугольника (p = (a + b + c) / 2), то выражение для радиуса r можно найти по формуле r = sqrt(p(p - a)(p - b)(p - c)) / p,

где a, b и c - длины сторон треугольника.

Используя эти методы, можно построить вписанную окружность в прямоугольный треугольник без необходимости измерять его стороны и радиус.

Методы на основе длин сторон и координат

Существуют различные методы для построения вписанной окружности в прямоугольный треугольник без измерений. Один из таких методов основан на известных длинах сторон треугольника.

Для начала, найдем полупериметр треугольника, который вычисляется как сумма длин всех трех сторон, деленная на 2. Полупериметр обозначается как p.

Затем, вычислим радиус вписанной окружности, используя формулу:r = A / p, где A - площадь треугольника, которая может быть вычислена через формулу герона:A = sqrt(p * (p - a) * (p - b) * (p - c)), где a, b и c - длины сторон треугольника.

Таким образом, зная длины сторон треугольника, можно вычислить радиус вписанной окружности.

Другой метод основан на координатах вершин треугольника. Для этого необходимо знать координаты вершин треугольника.

Сначала находим середины сторон треугольника, которые можно вычислить, используя формулы:

x_m1 = (x_a + x_b) / 2, y_m1 = (y_a + y_b) / 2 для стороны AB,

x_m2 = (x_b + x_c) / 2, y_m2 = (y_b + y_c) / 2 для стороны BC,

x_m3 = (x_c + x_a) / 2, y_m3 = (y_c + y_a) / 2 для стороны CA.

Затем, вычисляем перпендикулярные биссектрисы трех сторон треугольника, которые проходят через соответствующие середины сторон. Биссектрисы могут быть найдены, используя формулы:

y = k₁ * x + b₁ для биссектрисы стороны AB,

y = k₂ * x + b₂ для биссектрисы стороны BC,

y = k₃ * x + b₃ для биссектрисы стороны CA,

где k₁, k₂ и k₃ - коэффициенты наклона биссектрис, которые могут быть вычислены как:

k₁ = -1 / k_AB, где k_AB - наклон стороны AB,

k₂ = -1 / k_BC, где k_BC - наклон стороны BC,

k₃ = -1 / k_CA, где k_CA - наклон стороны CA.

Найденные уравнения биссектрис пересекаются в центре вписанной окружности. Координаты центра окружности могут быть найдены как точка пересечения трех уравнений биссектрис.

Используя один из этих методов, можно построить вписанную окружность в прямоугольный треугольник без измерений.

Шаги построения вписанной окружности в прямоугольный треугольник без измерений

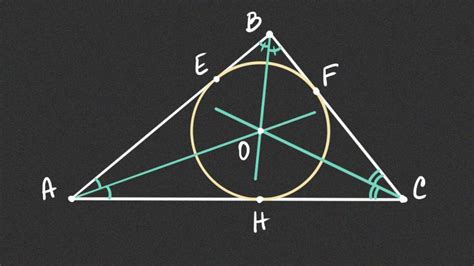
Построение вписанной окружности в прямоугольный треугольник без измерений возможно с использованием некоторых базовых геометрических конструкций. Ниже представлены шаги, которые помогут вам построить вписанную окружность в прямоугольный треугольник без использования измерительных инструментов.

Шаг 1: Нарисуйте прямоугольный треугольник на листе бумаги.

Шаг 2: На самом большом из трех углов прямоугольного треугольника постройте перпендикулярную линию, пересекающую стороны треугольника.

Шаг 3: На каждой из оставшихся сторон треугольника постройте перпендикулярную линию, проходящую через середину соответствующей стороны.

Шаг 4: Пересечение перпендикулярных линий, построенных в предыдущем шаге, определит центр вписанной окружности.

Шаг 5: Соедините центр окружности с каждым из вершин треугольника.

Шаг 6: Постройте отрезки, соединяющие центр окружности с точками пересечения сторон треугольника с окружностью.

Шаг 7: Отметьте точки пересечения отрезков, построенных в предыдущем шаге, с вершинами треугольника.

Шаг 8: Отметьте точку пересечения каждой из боковых сторон треугольника с противолежащей стороной.

Шаг 9: Все отмеченные точки являются точками касания вписанной окружности с треугольником.

Пользуясь этими шагами, вы можете построить вписанную окружность в прямоугольный треугольник без измерений.

Нахождение биссектрисы треугольника

Существует несколько способов нахождения биссектрисы треугольника:

1. Способ 1: Используя формулу для нахождения длины биссектрисы: l = 2 * sqrt(ab * bc * ac / (ab + ac + bc)), где ab, bc и ac - длины сторон треугольника. Затем проводим прямую из вершины треугольника к середине противолежащей стороны, равной полученной длине l.
2. Способ 2: Рассматривая угол между двумя сторонами треугольника и прямой, проведенной из вершины треугольника к середине третьей стороны. Эта прямая будет являться биссектрисой угла. Для построения можно использовать циркуль или ножницы-ножницы.
3. Способ 3: Находя точку пересечения высот треугольника. Провести две высоты из двух вершин треугольника и найти их точку пересечения. Прямая, проходящая через эту точку и середину противоположной стороны, будет являться биссектрисой угла.

Используя эти методы, можно находить биссектрису треугольника без измерений, только знание сторон и углов треугольника. Это позволяет строить вписанную окружность в прямоугольный треугольник без измерений.

Нахождение точек пересечения биссектрисы со сторонами треугольника

Биссектриса разделяет угол треугольника на две равные части. Для нахождения точек пересечения биссектрисы с каждой из сторон треугольника, нужно выполнить следующие шаги:

1. Построить биссектрису угла треугольника. Для этого проведите линию, которая делит угол на равные части.
2. Продлите биссектрису до пересечения с первой стороной треугольника.
3. Проведите перпендикуляр к первой стороне, проходящий через точку пересечения биссектрисы и первой стороны.
4. Полученная точка пересечения является одним из точек касания окружности с треугольником.
5. Аналогичные шаги повторите для второй стороны треугольника, чтобы найти вторую точку пересечения биссектрисы со стороной.

Точки пересечения биссектрисы с каждой из сторон треугольника будут являться точками касания вписанной окружности с треугольником. Для построения вписанной окружности необходимо провести окружность с радиусом, равным расстоянию от центра окружности до любой из точек касания.

Нахождение центра окружности через точки пересечения биссектрисы

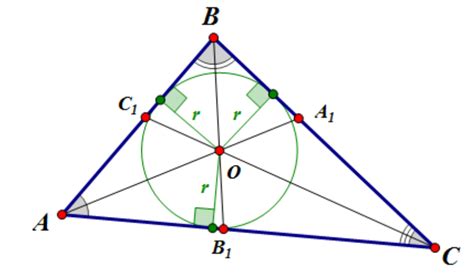
Для начала построим прямую, которая будет являться биссектрисой одного из углов прямоугольного треугольника. Для этого проведем прямую через вершину угла и точку пересечения противоположной стороны с высотой, опущенной из вершины этого угла. Полученная прямая будет являться биссектрисой угла.

Затем, найдем такую же биссектрису для другого угла прямоугольного треугольника. Это можно сделать аналогично -- проведя прямую через вершину угла и точку пересечения противоположной стороны с высотой, опущенной из вершины этого угла.

Теперь найдем точку пересечения двух биссектрис. Она будет являться центром вписанной окружности.

Для построения окружности можно воспользоваться следующим алгоритмом:

1. Найдите середину одной из сторон прямоугольного треугольника и обозначьте ее точкой A.
2. Укажите точкой B вершину прямого угла треугольника.
3. Умножьте расстояние между точкой A и B на 2, чтобы найти длину гипотенузы прямоугольного треугольника.
4. Найдите середину гипотенузы и обозначьте ее точкой C.
5. Постройте окружность с центром в точке C и радиусом, равным длине гипотенузы, поделенной на 2.
6. Исходный прямоугольный треугольник будет полностью охватываться этой окружностью.

Таким образом, используя точки пересечения биссектрисы и следуя описанному алгоритму, можно построить вписанную окружность в прямоугольный треугольник без измерений.