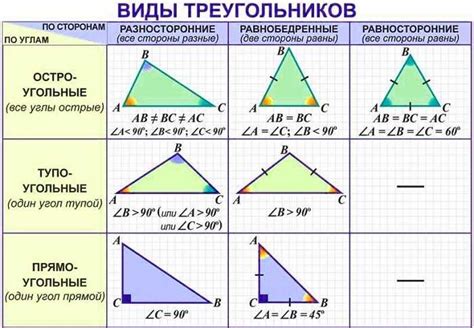
Остроугольный треугольник - это треугольник, у которого все углы острые, то есть меньше 90 градусов. В этом треугольнике особенно интересная характеристика - это высота. Высота - это отрезок, проведенный из вершины треугольника на прямую, перпендикулярную основанию. Как построить высоту на остроугольном треугольнике? В этой статье мы рассмотрим несколько способов для этого.
Первый способ - это строительство высоты через середину основания. Для этого нужно найти середину одной из сторон, а затем провести через нее прямую, перпендикулярную этой стороне. Таким образом, мы получим высоту треугольника. Этот способ особенно удобен, если у нас есть линейка и карандаш.
Второй способ - это построение высоты с использованием понятия "ортоцентра". Ортоцентр - это точка пересечения высот треугольника. Для построения высоты нужно провести высоты из каждой вершины треугольника и найти их точку пересечения - ортоцентр. От ортоцентра проводим высоту к основанию треугольника. Этот способ особенно интересен с геометрической точки зрения, но требует некоторого опыта в построении геометрических фигур.
Независимо от выбранного способа, построение высоты на остроугольном треугольнике позволяет нам лучше узнать его свойства и особенности. Эта простая геометрическая операция помогает нам лучше понять и восхититься математическим миром. Для проведения построений рекомендуется использовать точные инструменты, такие как линейка и угольник.
Как разбить остроугольный треугольник на высоты
- Выберите одну из сторон треугольника.
- Проведите перпендикулярную прямую из вершины, не принадлежащей выбранной стороне.
- Пересечение этой прямой с выбранной стороной будет точкой пересечения исходной стороны с высотой.
- Повторите шаги 1-3 для каждой из оставшихся сторон треугольника.
После выполнения этих шагов внутри остроугольного треугольника будут построены три высоты, которые пересекаются в одной точке – ортоцентре треугольника. Разбиение треугольника на высоты позволяет найти точки пересечения сторон с высотами и вычислить площадь треугольника с помощью формулы S=½ah, где a – длина основания, h – высота треугольника.
Разбиение остроугольного треугольника на высоты является важной операцией в геометрии и находит применение в различных задачах и расчетах, например, при изучении прямоугольных треугольников или в решении задач градостроительства.
Остроугольный треугольник – основные понятия и свойства
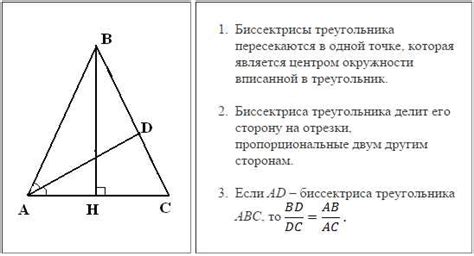
Основные свойства остроугольного треугольника:
1. Сумма углов в треугольнике
В остроугольном треугольнике сумма всех углов равна 180 градусов. Таким образом, каждый из трех острых углов будет меньше 90 градусов.
2. Стороны треугольника
Стороны остроугольного треугольника могут быть разной длины, но все они положительные. Остроугольный треугольник не может иметь отрицательные стороны или нулевую длину.
3. Высота треугольника
Высота остроугольного треугольника – это перпендикуляр, опущенный из вершины треугольника на противоположную сторону. Высота делит треугольник на две равные по площади части и является основой различных геометрических задач, таких как нахождение площади треугольника или определение биссектрисы угла.
Остроугольные треугольники являются важным объектом изучения в геометрии. Они обладают множеством интересных свойств и являются основой для различных геометрических задач и теорем.
Способы построения высот в остроугольном треугольнике
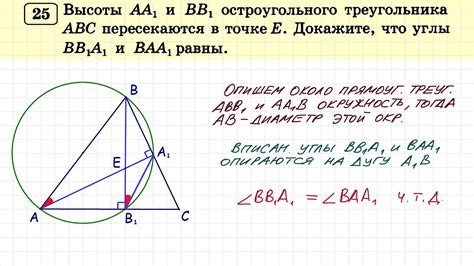
- Перпендикуляр из вершины – самый простой и широко используемый способ. Чтобы построить высоту из вершины A, проводят перпендикуляр к противоположной стороне BC.
- Проведение прямой через центр окружности – во всех треугольниках, в том числе и в остроугольных, существует окружность, которая может быть построена на основе сторон треугольника. Через центр этой окружности можно провести высоту к противоположной стороне.
- Использование медианы и определение прямоугольного треугольника – в остроугольном треугольнике есть особенность: сумма квадратов длин двух медиан делится на половину квадрата третьей медианы. Это свойство можно использовать для определения высот.
- Использование теоремы косинусов – это математический подход, позволяющий определить длину высоты с использованием длин сторон треугольника и косинуса угла между этой стороной и противоположной ей стороной.
Высоты остроугольного треугольника имеют множество применений в геометрии и других областях, таких как физика, архитектура и инженерия. Знание способов построения высот помогает решать задачи, связанные с данным типом треугольника.
Зависимость высот от сторон остроугольного треугольника
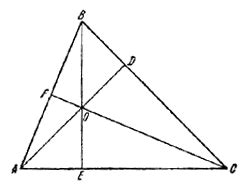
Зависимость высот от сторон остроугольного треугольника может быть выражена следующим образом:
Высота, проведенная из вершины с углом α, пропорциональна стороне, противолежащей этому углу.
Формула для вычисления длины высоты из вершины A с углом α, противолежащей стороне a, будет выглядеть следующим образом:
hA = a * sinα
где hA - длина высоты из вершины A, a - длина стороны, α - угол между сторонами b и c.
Аналогично, высота из вершины B будет зависеть от стороны b, и высота из вершины C - от стороны c.
Зная зависимость между высотами и сторонами остроугольного треугольника, можно провести высоты и решить различные задачи, связанные с этими треугольниками.
Применение высот остроугольного треугольника в геометрии и практических задачах
Применение высот остроугольного треугольника в геометрии:
| Свойство | Определение |
|---|---|
| Перпендикулярность | Каждая высота остроугольного треугольника перпендикулярна соответствующей стороне и проходит через вершину треугольника, к которой непосредственно относится. |
| Вписанность | Точка пересечения высот остроугольного треугольника является центром окружности, вписанной в данный треугольник. |
| Равенство длин | В остроугольном треугольнике длины высот равны между собой и обратно пропорциональны длинам сторон треугольника. |
Применение высот остроугольного треугольника в практических задачах:
1. Высоты остроугольного треугольника используются для нахождения площади треугольника. Площадь треугольника можно найти, зная длину одной из сторон и соответствующую высоту.
2. Высоты остроугольного треугольника используются при решении задач на нахождение расстояния от вершины треугольника до прямой, параллельной одной из сторон треугольника. Для этого необходимо провести высоту, перпендикулярную выбранной стороне, и найти высоту, проходящую через искомую точку.
3. Высоты остроугольного треугольника применяются в задачах на нахождение углов треугольника по заданным сторонам и высотам. Зная значения сторон и высот, можно найти все острые углы треугольника, используя соответствующие тригонометрические функции.
Таким образом, высоты остроугольного треугольника являются важным элементом в геометрии и применяются в решении разнообразных практических задач, связанных с треугольниками.