Ромб является одним из простейших и наиболее интересных геометрических фигур. Он имеет ряд уникальных свойств и применяется в различных областях, начиная от архитектуры и дизайна, и заканчивая наушниками, украшениями и игровыми предметами. Одним из самых важных параметров ромба является его высота, которая может быть рассчитана по определенной формуле.
Для построения высоты ромба необходимо знать длину двух его сторон. Пусть a и b - длины сторон ромба. Высота ромба может быть рассчитана по формуле:
h = (2 * A) / a, где h - высота ромба, A - площадь ромба, a - длина одной из его сторон.
Давайте рассмотрим пример. Пусть у нас есть ромб со стороной a = 4 и площадью A = 8. Подставив значения в формулу, получим:
h = (2 * 8) / 4 = 16 / 4 = 4.
Таким образом, высота ромба равна 4 единицам.
Как построить высоту ромба: пошаговая инструкция и примеры

Для построения высоты ромба следуйте следующей пошаговой инструкции:
- На картоне или листе бумаги постройте основание ромба, нарисовав две пересекающиеся прямые линии.
- Выберите одну из точек пересечения линий и назовите ее A. Она будет являться вершиной ромба.
- Выберите другую точку пересечения линий и назовите ее B.
- Соедините точки A и B прямой линией, чтобы получить одну из сторон ромба.
- На стороне AB выберите произвольную точку и назовите ее C.
- Проведите прямую линию, проходящую через точку C и перпендикулярную стороне AB.
- Пересечение прямых AB и CD будет являться вершиной D ромба.
- Таким образом, прямая линия, которая соединяет вершины A и D, является высотой ромба.
Для визуализации процесса построения высоты ромба рассмотрим следующий пример:
На рисунке изображена основа ромба, состоящая из двух пересекающихся прямых линий.
Шаг 1:
A | | |___________ B
На рисунке видно, что мы выбрали точку A в качестве вершины ромба и точку B на основании.
Шаг 2:
A | | | B
Далее мы соединяем точки A и B прямой линией и продолжаем с построением высоты.
Шаг 3:
A |\ | \ | \ B
На стороне AB мы выбираем произвольную точку C.
Шаг 4:
A |\ | \ | \ C B
Затем проводим прямую, проходящую через точку C и перпендикулярную стороне AB.
Шаг 5:
A |\ | \ | \ C--D B
Точка D - это пересечение прямых AB и CD. Таким образом, линия AD является высотой ромба.
Построение высоты ромба позволяет найти расстояние от одной вершины ромба до противоположной стороны. Это может быть полезно при решении различных геометрических задач.
Важно помнить: при построении высоты ромба необходимо следить за правильным выбором точек и проведением прямых линий. Тщательное следование инструкции поможет вам получить точный результат.
Шаг 1: Определите длину стороны ромба
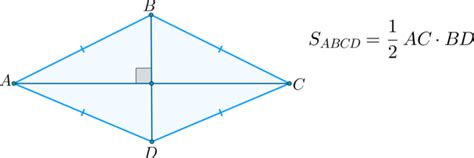
Если вам известны оба измерения, например, длина одной диагонали и периметр, вы можете использовать эти значения для нахождения длины стороны ромба.
Если у вас есть только одно измерение, например, длина одной диагонали, можно использовать специальные формулы, чтобы найти длину стороны ромба.
Если у вас нет известных измерений, вам потребуется дополнительная информация или математические расчеты для определения длины стороны ромба.
Когда вы определили длину стороны ромба, вы можете переходить ко второму шагу - построению высоты ромба.
| Первое измерение: | Длина одной диагонали и периметр |
| Формула: | Если известна длина одной диагонали (d) и периметр (P), можно использовать формулу P = 4a, где a - длина стороны ромба. |
| Второе измерение: | Длина одной диагонали |
| Формула: | Если известна длина одной диагонали (d), можно использовать формулу a = d / √2, где a - длина стороны ромба. |
| Дополнительная информация: | Дополнительные измерения или математические расчеты |
Шаг 2: Найдите диагонали ромба
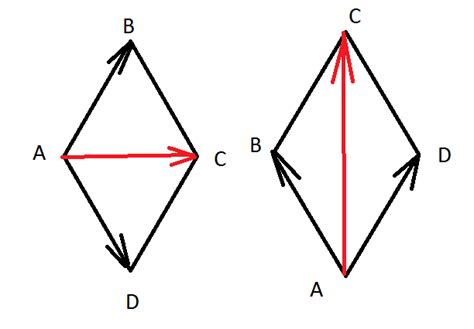
1. Зная длины сторон ромба, можно найти длины его диагоналей с помощью теоремы Пифагора. По теореме Пифагора сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины гипотенузы. В ромбе правильный прямоугольный треугольник образуется с помощью диагоналей и одной стороны ромба.
2. Диагонали ромба делят его на четыре равных треугольника. Если известны длины сторон ромба, можно использовать теорему Пифагора для нахождения длин диагоналей. После нахождения длин диагоналей, можно найти высоту ромба как прямую, проведенную из вершины ромба к прямой, содержащей диагональ ромба.