Производная функции - это одно из важнейших понятий в математике. На практике это позволяет найти скорость изменения функции в каждой точке графика, а также определить экстремумы функции. Квадратичные функции, которые представляют собой уравнения вида f(x) = ax^2 + bx + c, являются особенно интересными и распространенными в алгебре и физике.
Однако найти производную квадратичной функции без ошибок может быть не так просто, особенно при работе с большими числами и сложными формулами. В этой статье мы рассмотрим несколько полезных методов и правил, которые помогут вам справиться с этой задачей, минимизируя возможность ошибок.
Первым шагом в нахождении производной квадратичной функции является запись функции в виде f(x) = ax^2 + bx + c. Здесь a, b и c - это константы, которые задают конкретную квадратичную функцию. Прежде чем выполнять дальнейшие вычисления, важно убедиться, что функция задана правильно и все коэффициенты верно записаны.
Далее, нам необходимо применить некоторые основные алгебраические правила для нахождения производной. Правило степенной функции гласит, что производная функции f(x) = x^n равна произведению ее степени на коэффициент при мономе (n * a).
Что такое производная квадратичной функции?
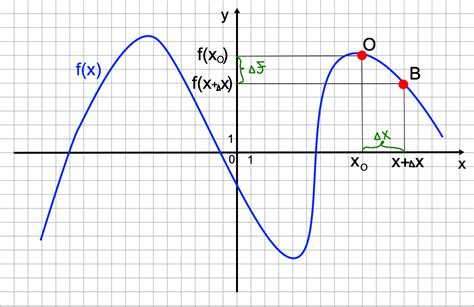
Производная квадратичной функции позволяет найти так называемый коэффициент наклона касательной линии к графику функции в каждой точке. Это позволяет понять, как быстро или медленно функция меняется в данной точке.
Производная функции f(x) обозначается как f'(x) или dy/dx. Её можно выразить аналитически с помощью дифференциального исчисления или вычислить численно, используя алгоритмы приближенного дифференцирования.
Производная квадратичной функции может принимать положительные и отрицательные значения, в зависимости от значения коэффициента a. Если a положительное, то производная положительна в вершине параболы и отрицательна вне её. Если a отрицательное, то производная отрицательна в вершине и положительна вне параболы.
Зачем нужно находить производную квадратичной функции?
Прежде всего, производная позволяет нам определить скорость изменения квадратичной функции в каждой точке ее графика. Это может быть полезно, например, при изучении движения тела или анализе траекторий.
Кроме того, нахождение производной может помочь нам найти точки экстремума функции, такие как минимумы и максимумы. Это может быть полезно, например, при оптимизации задач или поиске наилучших решений.
Производная также позволяет нам анализировать выпуклость и вогнутость графика квадратичной функции. Это может быть полезно, например, при изучении поведения функции в зависимости от различных параметров.
Необходимо отметить, что нахождение производной квадратичной функции является основой для решения многих других математических задач. Поэтому умение находить производную без ошибок является важным навыком для студентов и профессионалов в разных областях науки и инженерии.
Шаг 1. Запишите квадратичную функцию в общей форме

Прежде чем найти производную квадратичной функции, необходимо записать ее в общей форме. Квадратичная функция имеет вид:
f(x) = ax^2 + bx + c
где a, b и c - коэффициенты функции.
Коэффициент a отвечает за выпуклость или вогнутость параболы. Если a > 0, парабола будет направлена вверх и будет выпуклой, если a < 0, то парабола будет направлена вниз и будет вогнутой.
Коэффициент b отвечает за смещение параболы вдоль оси x.
Коэффициент c определяет смещение параболы вдоль оси y.
Шаг 2. Примените правило производной квадратичной функции

Для каждого члена функции применяется правило производной:
- Для члена ax^2, где a - коэффициент, производная равна: 2ax.
- Для члена bx, где b - коэффициент, производная равна: b.
- Для члена c, где c - коэффициент, производная равна: 0.
После нахождения производных каждого члена функции, их суммируют или вычитают в зависимости от знаков коэффициентов перед членами функции. Таким образом, получается окончательная производная квадратичной функции.
Например, для функции f(x) = 3x^2 + 2x - 1 производная будет: f'(x) = (2 * 3x) + 2 = 6x + 2.
Теперь вы знаете, как применить правило производной квадратичной функции и найти производную без ошибок. Этот шаг поможет вам дальше в анализе функции и нахождении ее экстремумов или точек перегиба.
Шаг 3. Упростите полученное выражение

После нахождения производной квадратичной функции вам может понадобиться упростить полученное выражение. Упрощение поможет вам более четко видеть основные характеристики функции, такие как вершина и ось симметрии.
Для упрощения выражения, вначале вы можете объединить подобные слагаемые. Если у вас есть слагаемые с одинаковыми степенями переменной, вы можете складывать или вычитать их.
Затем вы можете раскрыть скобки и сократить подобные слагаемые. Учтите, что при этом вам нужно внимательно следить за знаками перед каждым членом выражения.
Далее вам нужно упростить выражение до окончательного вида, удаляя ненужные скобки и объединяя подобные слагаемые, если это возможно.
Упрощение выражения поможет вам получить наиболее удобный и понятный вид функции, который будет полезен при решении различных задач, связанных с графиками квадратичных функций.
| Пример упрощения: | Если у вас есть выражение 3x^2 + 2x - 5x^2 - 4x + 7, вы можете объединить подобные слагаемые, чтобы получить -2x^2 - 2x + 7. Затем вы можете раскрыть скобки и сократить подобные слагаемые, если они есть. В данном случае упрощение не требуется, так что окончательное выражение будет -2x^2 - 2x + 7. |
|---|
Шаг 4. Проверьте правильность результата
После того как вы получили производную квадратичной функции, необходимо проверить правильность результата, чтобы быть уверенным в его точности. Следуя этому шагу, вы сможете заметить и исправить возможные ошибки, которые могли возникнуть в процессе вычислений.
Для начала, убедитесь, что вы правильно применили правила дифференцирования к каждому члену функции. Проверьте, что вы правильно раскрыли скобки и упростили выражение перед вычислением производной.
Затем, рекомендуется рассмотреть выведенное выражение и сравнить его с оригинальной функцией. Подставьте значения переменных в оба выражения и сравните полученные результаты. Если вы получили одинаковые значения, то высока вероятность, что ваша производная вычислена правильно.
Дополнительно, вы можете использовать таблицу, чтобы проверить производную. Занесите значения переменных в таблицу и проделайте вычисления, используя полученную производную. Убедитесь, что новые значения совпадают с исходной функцией.
| Значение переменной | Оригинальная функция | Производная | Результат вычисления |
|---|---|---|---|
| x1 | f(x1) | f'(x1) | f'(x1) |
| x2 | f(x2) | f'(x2) | f'(x2) |
| x3 | f(x3) | f'(x3) | f'(x3) |
Если значения в последнем столбце совпадают с исходной функцией, то вы можете быть уверены в правильности полученной производной. Если же значения различаются, необходимо проанализировать каждый шаг вычисления и найти возможные ошибки.
Проверка правильности результата является важным шагом в процессе нахождения производной квадратичной функции. Будьте внимательны и тщательны при выполнении данного шага, чтобы избежать возможных ошибок и получить точный результат.