Треугольник – это одна из первых и наиболее простых геометрических фигур, изучаемая уже в школьные годы. Но как построить треугольник, если известны только его стороны? В этой статье мы рассмотрим правила и методы конструирования треугольника по трем сторонам.
Для начала, давайте разберемся, какие условия должны быть выполнены для того, чтобы треугольник существовал. Оказывается, что существует неравенство для длин сторон треугольника, которое называется неравенством треугольника. Согласно этому неравенству, сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны.
Исходя из неравенства треугольника, мы можем приступить к конструированию треугольника по трем сторонам. Для этого существуют несколько методов, одним из которых является использование компаса и линейки. Данная техника требует точности и внимательности, но позволяет получить точный результат.
Конструирование треугольника: правила и методы строительства
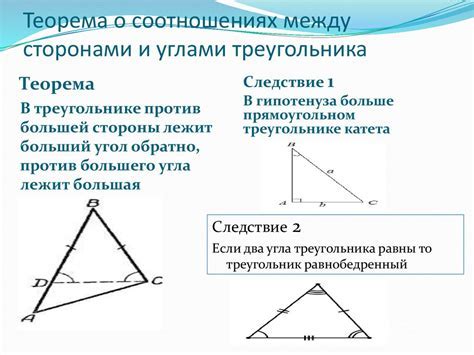
Для конструирования треугольника по трем сторонам существуют определенные правила и методы, которые помогают точно определить его форму и размеры. Вот основные правила и методы строительства треугольника:
- Проверка существования треугольника.
- Построение биссектрисы.
- Построение высоты.
- Построение медианы.
- Построение ортоцентра.
Перед началом конструирования треугольника необходимо проверить существование такого треугольника, основываясь на длинах заданных сторон. Если сумма двух сторон меньше третьей стороны или если все три стороны равны нулю или отрицательны, то треугольник не существует.
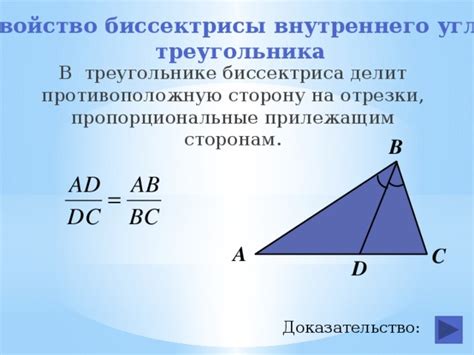
Построение биссектрисы является одним из методов строительства треугольника. Биссектрисой называется прямая, которая делит угол треугольника на две равные части. Чтобы построить биссектрису, нужно провести дуги радиусом, равным длине одной из сторон треугольника, с центром в вершине угла. Точка пересечения дуг будет серединой биссектрисы.
Другой метод строительства треугольника – построение высоты. Высотой называется отрезок, проведенный из вершины треугольника до прямой, содержащей противоположную сторону треугольника и перпендикулярной к ней. Для построения высоты можно провести прямую через вершину и середину противоположной стороны треугольника.
Построение медианы – еще один метод строительства треугольника. Медианой является отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Для построения медианы необходимо провести прямую через вершину и середину противоположной стороны треугольника.
Ортоцентр треугольника – точка пересечения трех высот треугольника. Для построения ортоцентра нужно провести высоты треугольника и найти точку их пересечения.
Это лишь некоторые правила и методы конструирования треугольника по трем сторонам. Геометрические конструкции позволяют описывать и анализировать пространственные формы и свойства треугольников.
Определение сторон треугольника
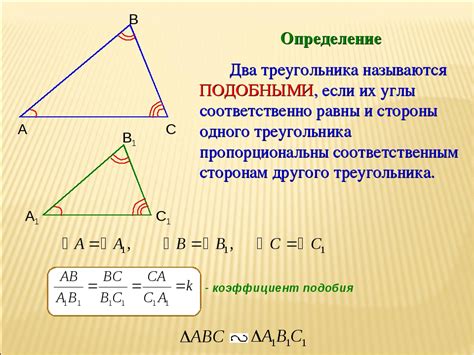
Для конструирования треугольника по заданным трем сторонам необходимо знать их длины. Для этого можно использовать специальные инструменты, такие как линейка или штангенциркуль.
После того как длины сторон измерены, следует проверить выполнение неравенства треугольника: сумма любых двух сторон должна быть больше третьей стороны. Если это условие выполняется, то треугольник можно построить.
| Сторона | Длина, см |
|---|---|
| AB | 5 |
| BC | 6 |
| AC | 7 |
В данном примере длины сторон треугольника равны: AB = 5 см, BC = 6 см, AC = 7 см. Проверим выполнение неравенства треугольника:
AB + BC = 5 + 6 = 11 > AC
AB + AC = 5 + 7 = 12 > BC
BC + AC = 6 + 7 = 13 > AB
Таким образом, неравенство треугольника выполняется, и по заданным значениям сторон треугольник можно построить.
Условия строительства треугольника
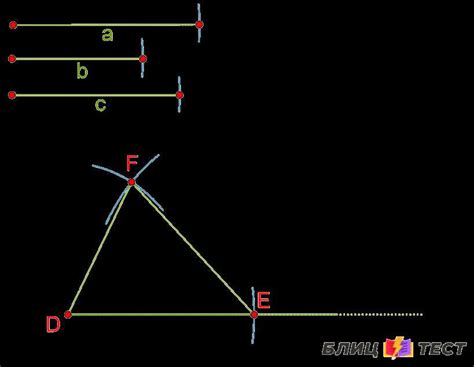
Для того чтобы сконструировать треугольник по трем сторонам, необходимо учитывать следующие условия:
- Длина каждой стороны треугольника должна быть больше нуля;
- Сумма двух любых сторон треугольника должна быть больше третьей стороны;
- Разность двух любых сторон треугольника должна быть меньше третьей стороны.
Если данные условия не выполняются, треугольник с такими сторонами невозможно построить.
Главные правила треугольника
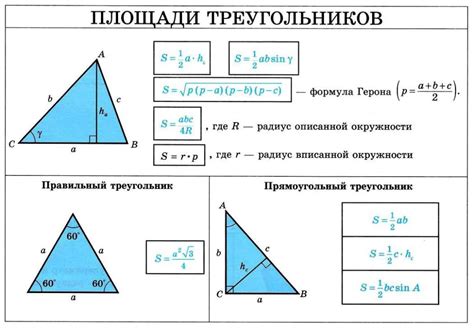
При конструировании треугольника по трем сторонам необходимо учитывать следующие основные правила:
- Сумма двух сторон треугольника всегда должна быть больше третьей стороны. Иначе треугольник не может существовать.
- Разность двух сторон треугольника всегда должна быть меньше третьей стороны. Если эта разность равна третьей стороне, то получается вырожденный треугольник.
- Длина каждой стороны треугольника всегда должна быть положительным числом.
- Сумма трех углов треугольника всегда должна равняться 180 градусам.
- Стороны треугольника могут быть любой длины, при условии соблюдения основных правил.
Правильное применение этих правил обеспечивает построение корректного треугольника по трем заданным сторонам.
Методы конструирования треугольника
Существует несколько методов для конструирования треугольника по трем сторонам:
| Метод | Описание |
|---|---|
| 1. Метод использования линейки и циркуля или других инструментов для построения | Данный метод является самым точным и детальным, но требует специальных инструментов и навыков работы с ними. Он основан на применении циркуля и линейки для построения углов и отрезков с заданными длинами. Это позволяет точно определить и построить треугольник заданных размеров. |
| 2. Метод построения при помощи угломера | Для этого метода используется угломер – инструмент с двумя подвижными рейками, которые могут поворачиваться друг относительно друга. Угломером можно измерить углы между сторонами треугольника, а затем точно построить треугольник используя эти углы. |
| 3. Метод путем вычисления с учетом построенного угла | Этот метод требует знания методов тригонометрии и применения угловых формул для вычисления длины отсутствующей стороны, если две стороны и угол между ними известны. Обратная задача также может быть выполнена в этом методе: при наличии трех сторон, используя тригонометрические формулы можно вычислить углы треугольника. |
Выбор метода конструирования треугольника зависит от доступных инструментов и навыков человека, который планирует выполнить конструкцию. Важно помнить, что правильное и точное выполнение конструирования требует аккуратности и внимания к деталям.