У вас есть равнобедренная трапеция, и вы хотите вычислить ее диагональ? Вы находитесь в правильном месте! Вычисление диагонали равнобедренной трапеции может показаться сложным на первый взгляд, но на самом деле это довольно просто. В этой статье мы расскажем, как вычислить диагональ равнобедренной трапеции и предоставим вам несколько примеров, чтобы помочь вам лучше понять эту концепцию.

Прежде чем мы начнем, давайте разберемся в определении равнобедренной трапеции. Равнобедренная трапеция - это четырехугольник с двумя параллельными сторонами, из которых одна пара называется основанием, а другая - боковыми сторонами. Боковые стороны равнобедренной трапеции имеют одинаковую длину, а углы между основанием и боковыми сторонами также равны.

Теперь, когда мы понимаем, что такое равнобедренная трапеция, давайте перейдем к вычислению ее диагонали. Для этого существует простая формула. Если мы обозначим основания трапеции как "a" и "b", а диагональ как "d", то формула для вычисления диагонали равнобедренной трапеции будет выглядеть следующим образом:

d = √(a^2 + b^2)

В этой формуле "√" обозначает квадратный корень, а "^" обозначает возведение в степень. Просто подставьте известные значения оснований и вычислите квадратный корень от суммы их квадратов. Вот и все! Теперь у вас есть несложный способ вычисления диагонали равнобедренной трапеции.

Как вычислить диагональ равнобедренной трапеции

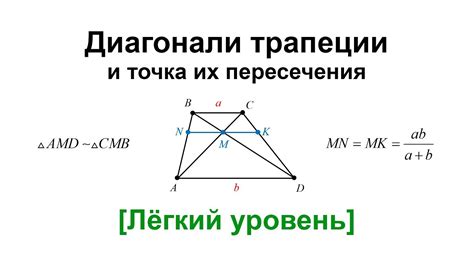
Формула для вычисления диагонали равнобедренной трапеции имеет вид:

d = 2 * √((a^2 + b^2) / 4 - h^2)

где:

• d - диагональ равнобедренной трапеции;
• a и b - основания трапеции;
• h - высота трапеции.

Для вычисления диагонали необходимо знать значения оснований и высоты трапеции. Зная эти значения, можно подставить их в формулу и получить результат.

Например, пусть основание трапеции равно 8 см, второе основание равно 6 см, а высота составляет 4 см:

d = 2 * √((8^2 + 6^2) / 4 - 4^2)

d = 2 * √((64 + 36) / 4 - 16)

d = 2 * √(100 / 4 - 16)

d = 2 * √(25 - 16)

d = 2 * √(9) = 2 * 3 = 6

Таким образом, диагональ равнобедренной трапеции в данном примере равна 6 см.

Простое объяснение и формула

Для определения длины диагонали равнобедренной трапеции можно использовать следующую формулу:

диагональ = √(основание₁² + основание₂² + 2 × высота²)

Здесь основание₁ и основание₂ - длины оснований трапеции, а высота - расстояние между ними.

Приведенная формула основана на теореме Пифагора. Если мы представим основания и диагонали трапеции как стороны прямоугольного треугольника, то длина диагонали будет являться гипотенузой этого треугольника.

Таким образом, чтобы вычислить диагональ равнобедренной трапеции, нужно знать длины оснований и высоту.

Определение равнобедренной трапеции

Основания равнобедренной трапеции - это две параллельные стороны, которые не являются боковыми сторонами.

Боковые стороны равнобедренной трапеции - это две стороны, соединяющие основания и называемые также боковыми.

Высота равнобедренной трапеции - это отрезок, который соединяет перпендикулярно основания трапеции и проходит через острый угол между боковыми сторонами.

Зная основания и высоту равнобедренной трапеции, можно вычислить диагональ, используя соответствующую формулу.

Как вычислить длины боковых сторон

Для вычисления длин боковых сторон равнобедренной трапеции, нужно знать длину оснований и высоту.

Длина боковых сторон треугольника может быть вычислена по формуле:

сторона = sqrt(h^2 + (a - b)^2),

где h - высота трапеции,

a - длина большего основания,

b - длина меньшего основания.

Например, если известны значения h = 5, a = 10 и b = 6, то длина боковых сторон будет:

сторона1 = sqrt(5^2 + (10 - 6)^2) = sqrt(25 + 16) = sqrt(41) ≈ 6.40,

сторона2 = sqrt(5^2 + (6 - 10)^2) = sqrt(25 + 16) = sqrt(41) ≈ 6.40.

Таким образом, длины боковых сторон равнобедренной трапеции с высотой 5 единиц и основаниями длиной 10 и 6 единиц будут примерно равны 6.40 единицы.

Как найти высоту равнобедренной трапеции

Существует несколько способов нахождения высоты равнобедренной трапеции:

1. По формуле: h = √(c^2 - a^2/4), где h - высота, c - длина боковой стороны, a - длина основания.
2. Используя теорему Пифагора, если известны длины боковой стороны (c) и основания (a). В этом случае можно найти длину высоты, используя соотношение: h = √(c^2 - (a/2)^2).

Когда вы находите высоту равнобедренной трапеции, помните, что длина основания трапеции должна быть больше длины стороны и меньше суммы длин оснований. Также не забывайте, что длина высоты всегда будет меньше длины любой из оснований.

Формула для вычисления диагонали

Для вычисления диагонали равнобедренной трапеции с известными основаниями и углом между основаниями можно использовать следующую формулу:

Диагональ = √(боковая сторона² + ((основание₂ - основание₁) ÷ 2)²)

В этой формуле, боковая сторона - это одна из двух равных сторон равнобедренной трапеции, основание₁ и основание₂ - длины двух оснований трапеции, а угол между основаниями - это угол, образованный этими основаниями.

Применение этой формулы позволяет вычислить диагональ равнобедренной трапеции и получить точное числовое значение.